File:Ackerplot400.jpg
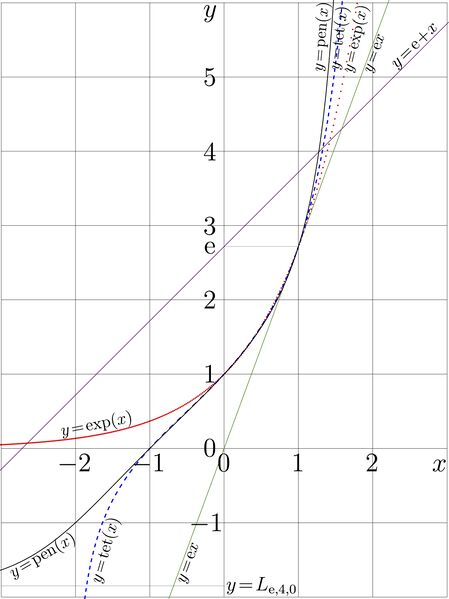
Explicit plot of the 5 Ackermann functions to base $\mathrm e$
$y=A_{\mathrm e,n}(x)~$ for $n=1,2,3,4,5$
$A_{\mathrm e,1}(z)=\mathrm e + z$
$A_{\mathrm e,2}(z)=\mathrm e \,z$
$A_{\mathrm e,3}(z)=\mathrm e^z~$ , see exp
$A_{\mathrm e,4}(z)=\mathrm{tet}(z)~$ , see natural tetration
$A_{\mathrm e,5}(z)=\mathrm{pen}(z)~$ , see natural pentation
Contents
General properties of Ackermann functions
The Ackermann function, or ackermann, to base $b$ satisfies the transfer equation
$A_{b,n}(z\!+\!1)=A_{b,n-1}\big( A_{b,n}(z) \Big)$
and the "initial" conditions $~A_{b,1}(z)\!=\!b\!+\!z~$, $~~A_{b,n}(1)\!=\!b$ for $n\!>\!1$
These conditions are not sufficient to provide the uniqueness of the ackermanns. The holomorphism with respect to the argument should be also required.
$n$ is interpreted as number of the ackermann; is supposed to be natural number.
For real base $b$, the ackermann is real-holomorphic, $A_{b,n}(z^*)=A_{b,n}(z)^*$.
C++ generator of curves
Files fsexp.cin and fslog.cin should be loaded in order to compile the code below.
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
#include <complex>
typedef std::complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
// #include "ado.cin"
void ado(FILE *O, int X, int Y)
{ fprintf(O,"%c!PS-Adobe-2.0 EPSF-2.0\n",'%');
fprintf(O,"%c%cBoundingBox: 0 0 %d %d\n",'%','%',X,Y);
fprintf(O,"/M {moveto} bind def\n");
fprintf(O,"/L {lineto} bind def\n");
fprintf(O,"/S {stroke} bind def\n");
fprintf(O,"/s {show newpath} bind def\n");
fprintf(O,"/C {closepath} bind def\n");
fprintf(O,"/F {fill} bind def\n");
fprintf(O,"/o {.01 0 360 arc C F} bind def\n");
fprintf(O,"/times-Roman findfont 20 scalefont setfont\n");
fprintf(O,"/W {setlinewidth} bind def\n");
fprintf(O,"/RGB {setrgbcolor} bind def\n");}
/* end of routine */
#include "fsexp.cin"
#include "fslog.cin"
z_type pen0(z_type z){ DB Lp=-1.8503545290271812; DB k,a,b;
k=1.86573322821; a=-.6263241; b=0.4827;
z_type e=exp(k*z); return Lp + e*(1.+e*(a+b*e)); }
z_type pen7(z_type z){ DB x; int m,n; z=pen0(z+(2.24817451898-7.));
DO(n,7) { if(Re(z)>8.) return 999.; z=FSEXP(z); if(abs(z)<40) goto L1; return 999.; L1: ;}
return z; }
z_type pen(z_type z){ DB x; int m,n;
x=Re(z); if(x<= -4.) return pen0(z);
m=int(x+5.);
z-=DB(m);
z=pen0(z);
DO(n,m) z=FSEXP(z);
return z;
}
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
FILE *o;o=fopen("ackerplo.eps","w"); ado(o,608,808);
fprintf(o,"304 204 translate\n 100 100 scale\n");
#define M(x,y) fprintf(o,"%8.4f %8.4f M\n",0.+x,0.+y);
#define L(x,y) fprintf(o,"%8.4f %8.4f L\n",0.+x,0.+y);
#define o(x,y) fprintf(o,"%8.4f %8.4f o\n",0.+x,0.+y);
for(m=-3;m<4;m++) {M(m,-2)L(m,6)}
for(n=-2;n<9;n++) {M( -3,n)L(3,n)} fprintf(o,"2 setlinecap 1 setlinejoin .004 W 0 0 0 RGB S\n");
M(-3.02,-3.02+M_E)L(3.02,3.02+M_E) fprintf(o,".007 W .3 0 .3 RGB S\n");
M(-1., -M_E)L(3.02,3.02*M_E) fprintf(o,".007 W 0 .5 0 RGB S\n");
//DO(n,156){x=-4+.04*n;y=exp(x); if(n==0) M(x,y)else L(x,y); if(y>7.)break;} fprintf(o,".02 W 0 .8 0 RGB S\n");
fprintf(o,"1 0 0 RGB\n");
DO(n,306){x=-3.02+.02*(n-.5);y=exp(x); o(x,y); if(y>6.)break;} fprintf(o,".02 W 0 .8 0 RGB S\n");
//DO(n,150){x=-1.9+.04*n;y=Re(FSEXP(x)); if(n==0) M(x,y)else L(x,y); if(y>8.)break;} fprintf(o,".02 W 0 0 1 RGB S\n");
DO(n,202){y=-3+.05*(n-.6);x=Re(FSLOG(y));
if(n/2*2==n) M(x,y)else L(x,y); if(y>6.)break;} fprintf(o,"0 setlinecap .016 W 0 0 1 RGB S\n");
DO(n,150){x=-3.03+.04*n;y=Re(pen7(x)); if(n==0) M(x,y)else L(x,y); if(y>6.)break;} fprintf(o,".01 W 0 0 0 RGB S\n");
DB L=-1.8503545290271812;
DB K=1.86573322821;
DB a=-.6263241;
DB b=0.4827;
M(-3,L)L(0,L)
M(0,M_E) L(1,M_E) fprintf(o,".002 W 0 0 0 RGB S\n");
//M(-4.1,-4.1+M_E) L(4.1,4.1+M_E) fprintf(o,".002 W 0 0 0 RGB S\n");
DB t2=M_PI/1.86573322821;
DB tx=-2.32;
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
printf("pen7(-1)=%18.14f\n", Re(pen7(-1.)));
printf("Pi/1.86573322821=%18.14f %18.14f\n", M_PI/1.86573322821, 2*M_PI/1.86573322821);
system("epstopdf ackerplo.eps");
system( "open ackerplo.pdf");
}
Latex generator of curves
\documentclass[12pt]{article}
\paperwidth 604px
\paperheight 806px
\textwidth 1394px
\textheight 1300px
\topmargin -104px
\oddsidemargin -92px
\usepackage{graphics}
\usepackage{rotating}
\newcommand \sx {\scalebox}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\newcommand \ing {\includegraphics}
\newcommand \rmi {\mathrm{i}}
\begin{document}
{\begin{picture}(608,806) %\put(12,0){\ing{penma}}
\put(0,0){\ing{ackerplo}}
\put(277,788){\sx{3.}{$y$}}
\put(277,695){\sx{3.}{$5$}}
\put(277,594){\sx{3.}{$4$}}
\put(277,494){\sx{3.}{$3$}}
\put(278,468){\sx{3.}{$\mathrm e$}}
\put(277,394){\sx{3.}{$2$}}
\put(277,294){\sx{3.}{$1$}}
\put(277,194){\sx{3.}{$0$}}
\put(258, 93){\sx{3.}{$-1$}}
\put( 80,174){\sx{3.}{$-2$}}
\put(180,174){\sx{3.}{$-1$}}
\put(296,174){\sx{3.}{$0$}}
\put(396,174){\sx{3.}{$1$}}
\put(496,174){\sx{3.}{$2$}}
\put(586,174){\sx{3.}{$x$}}
\put(438,714){\sx{1.8}{\rot{85}$y\!=\!\mathrm{pen}(x)$\ero}}
\put(460,716){\sx{1.8}{\rot{82}$y\!=\!\mathrm{tet}(x)$\ero}}
\put(478,712){\sx{1.8}{\rot{77}$y\!=\!\mathrm{exp}(x)$\ero}}
\put(504,712){\sx{1.8}{\rot{70}$y\!=\!\mathrm{e}x$\ero}}
%\put(478,628){\sx{1.8}{\rot{50}$y\!=\!\mathrm{e}\!+\!x$\ero}}
\put(538,718){\sx{1.96}{\rot{44}$y\!=\!\mathrm{e}\!+\!x$\ero}}
%
\put(86,222){\sx{1.9}{\rot{11}$y\!=\!\mathrm{exp}(x)$\ero}}
\put(20,30){\sx{1.9}{\rot{30}$y\!=\!\mathrm{pen}(x)$\ero}}
\put(138,22){\sx{1.9}{\rot{74}$y\!=\!\mathrm{tet}(x)$\ero}}
\put(252,22){\sx{1.9}{\rot{70}$y\!=\!\mathrm{e} x$\ero}}
%
\put(308, 13){\sx{2.2}{$y\!=\!L_{\mathrm e,4,0}$}}
\end{picture}
\end{document}
References
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670.
http://www.ils.uec.ac.jp/~dima/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45.
http://www.springerlink.com/content/u7327836m2850246/ H.Trappmann, D.Kouznetsov. Uniqueness of Analytic Abel Functions in Absence of a Real Fixed Point. Aequationes Mathematicae, v.81, p.65-76 (2011)
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 06:10, 1 December 2018 |  | 3,355 × 4,477 (805 KB) | Maintenance script (talk | contribs) | Importing image file |
- You cannot overwrite this file.
File usage
The following page links to this file: