Acosc1
Acosc1 is the holomorphic continuation of function ArcCosc behind the cut line along the negative part of the real axis.
Contents
Notations
In the text, this function appears with names ArcCosc1, or acosc1; in the formulas it may appear as \(\mathrm{acosc}_1\) to indicate that it defers to the first branch behind the cut line of function acosc, which could be called also by name \(\mathrm{acosc}_0\).
Properties of acosc1
\(f=\mathrm{Acosc1}(z)\) is solution of equation
- \( \displaystyle \mathrm{cosc}(f)=z\)
the same equation holds for ArcCosc and other branches acosc_n.
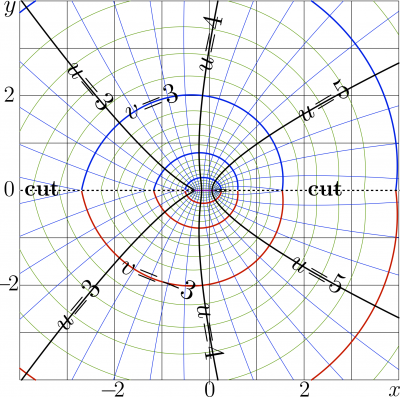
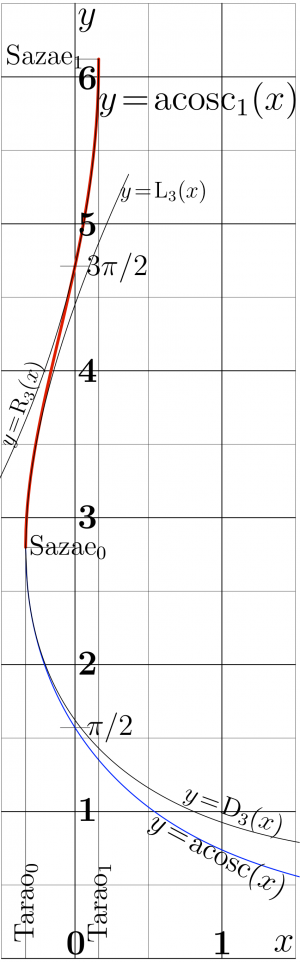
The Complex map of function acosc1 is shown in figure at top. The graphic for the real values of the argument is shown in the figure at right with thick red line; for comparison, in the same figure, function ArcCosc is shown with blue curve, and some asymptotics discussed below are shown with thin black lines.
Acosc1 has two branch points at
- Tarao\(_0 \approx −0.33650841691839534\)
and
- Tarao\(_1 \approx 0.161228034325064\)
The cut lines are directed along the real axis to \(-\infty\) and to \(\infty\).
Acosc1 is real holomorphic function; for all the branches numbered in this way, the relation below holds:
- \( \displaystyle \mathrm{acosc}_n(z^*) = \mathrm{acosc}_n(z)^*\)
At large values of argument, acosc1 shows logarithnig growth, similar to logarithm; however, the accurate handling of the branches is required to use this asymptotic for the evaluation.
In vicinity of its branch points, acosc1 can be asymptotically approximated with functions below, shown also in the figure:
- \(\displaystyle y= \mathrm R_3(x) = \mathrm{Sazae}_1 - \sqrt{ \frac{2}{\mathrm{Tarao}_1 } (\mathrm{Tarao}_1\!-\!x) } + \frac{2\, (\mathrm{Tarao}_1 \!-\! x )}{3~ \mathrm{Sazae}_1~ \mathrm{Tarao}_1}\)
which approximates the function in vicinity of \(\mathrm{Tarao}_1\), and
- \(\displaystyle y= \mathrm L_3(x) = \mathrm{Sazae}_0 + \sqrt{ \frac{-2}{\mathrm{Tarao}_0} (x-\mathrm{Tarao}_0) } - \frac {2\, (x\!-\!\mathrm{Tarao}_0)} {3~ \mathrm{Tarao}_0 ~ \mathrm{Sazae}_0} \)
which aprocimates the function in vicinity of Tarao\(=\mathrm{Tarao}_0\). These asymptotics are used in the numerical implementation acosc1 available at acosc1.cin. WIth Mathematica, one can easy calculate many terms of the expansions of the function at the branch points. The only 3 terms are kept in the approximations above to allow distinguish the approximations from acosc1 in the figure. The radius of convergence is equal to distance between the branch points; so, in vicinity of zero both series converge exponentially, and, with more terms in the truncation, overlap pretty well with exact acosc1, and also with the expansion at zero below.
For comparison, in the figure the approximation of ArcCosc is also shown:
- \(\displaystyle y= \mathrm L_3(x) = \mathrm{Sazae}_0 - \sqrt{ \frac{-2}{\mathrm{Tarao}_0} (x-\mathrm{Tarao}_0) } - \frac {2\, (x\!-\!\mathrm{Tarao}_0)} {3~ \mathrm{Tarao}_0 ~ \mathrm{Sazae}_0} \)
All the three approximations above look very similar; they give hint for the approximation of other branches of the inverse of function Cosc.
The expansion at zero can be written as follows:
- \( \displaystyle \mathrm{acosc}_1(z)= \frac{3 \pi}{2}+ \frac{3 \pi z}{2}+\frac{3 \pi z^2}{2} \) \( \displaystyle+\frac{3}{16} \pi \left(8+3 \pi ^2\right) z^3+\frac{3}{4} \pi \left(2+3 \pi ^2\right) z^4\) \( \displaystyle+\frac{3 \pi \left(640+2400 \pi ^2+243 \pi ^4\right) z^5}{1280}+\frac{3}{20} \pi \left(10+75 \pi ^2+27 \pi ^4\right) z^6\) \( \displaystyle+\frac{3 \pi \left(35840+470400 \pi ^2+391608 \pi ^4+18225 \pi ^6\right) z^7}{71680}\) \( \displaystyle+\frac{3}{560} \pi \left(280+5880 \pi ^2+9261 \pi ^4+1458 \pi ^6\right) z^8\) \( \displaystyle+\frac{3 \pi \left(1146880+36126720 \pi ^2+95510016 \pi ^4+33478272 \pi ^6+893025 \pi ^8\right) z^9}{2293760}\) \( \displaystyle+O\left(z^{10}\right) \)
Mathematica allows the straightforward calculation of a dozen of terms of such an expansion. The series converges at \(|z|<\mathrm{Tarao}_1 \approx 0.161228034325064\)
The first terms of this expansion can be used to evaluate the properties of the high modes of waves guided between absorbing walls at weak duping, id est, for the channeling conditions.
Argument rotated for phase \(\pi/4\)
At consideration of modes of atomic waves guided between absorbing walls, the branched of the inverse function of cosc appear with argument of phase \(\pi/4\). This makes reason to define function
- \( \mathrm{acosq}_n(z)= \mathrm{acosq}_n(z\, \mathrm e ^{\mathrm i \mathrm \pi /4} )\)
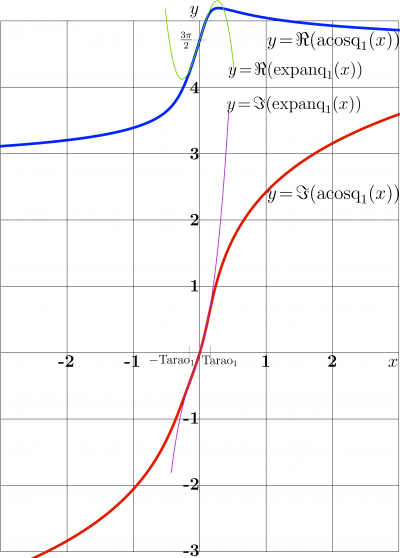
For \(n\!=\!1\), The explicit plot of the real and the imaginary parts of this function are plotted in figure at right. For comparison, the Taylor approximation with cubic polynomial is shown with thin lines,
- \( \displaystyle \mathrm{expan}_1(z) = \frac{3 \pi}{2}+ \frac{3 \pi z}{2}+\frac{3 \pi z^2}{2} \) \( \displaystyle+\frac{3}{16} \pi \left(8+3 \pi ^2\right) z^3\)
and, as for acosq,
- \( \mathrm{expanq}_1(z)= \mathrm{expan}_1(z \mathrm \, \mathrm{e}^{\mathrm i \mathrm \pi /4} )\)
While \(x\) is small compared to Tarao\(_1\), the linear approximation can be used.
Application and generalization
The transversal wavenumber \(p\) of \(n\)th mode guided between absorbing walls with the damping parameter \(\alpha\) is expressed with
- \( \displaystyle p=\mathrm{acosq}_n(\alpha)\)
In particular, at \(n\!=\!0\),
- \( \displaystyle \mathrm{acosq}_0(\alpha)= \mathrm{acosq}(\alpha)\)
and there is special article acosq for this case.
For the First mode (\(n\!=\!1\)), the good channeling conditions take place at \(~|\alpha|\! \ll\! \mathrm{Tarao_1}~\). In the figure, values \(~\pm \mathrm{Tarao}_1~\) are marked at the abscissa axis.
Keywords
Cos, Cosc, ArcCosc, ArcCosq, Inverse function, Channeling of waves between absorbing walls