Difference between revisions of "ArcCos"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| Line 1: | Line 1: | ||
| − | [[File:AcomapT200.png|400px|right|thumb|[[complex map]] of |
+ | [[File:AcomapT200.png|400px|right|thumb|[[complex map]] of \(u\!+\!\mathrm i v\!=\!\arccos(x\!+\!\mathrm i y)\)]] |
'''ArcCos''', or '''acos''' is [[holomorphic function]], inverse of [[cos]]. |
'''ArcCos''', or '''acos''' is [[holomorphic function]], inverse of [[cos]]. |
||
| Line 9: | Line 9: | ||
By definition, arccos is solution of equation |
By definition, arccos is solution of equation |
||
| − | : |
+ | : \( \cos(\arccos(z))=z\) |
==Range of holomorphism== |
==Range of holomorphism== |
||
| − | + | \(\arccos(z)\) is holomorphic in the whole complex plane except the halflines \(z\!\le\! -1\) and \(z\!\ge\! 1\). |
|
| − | Complex map or |
+ | Complex map or \(f=\arccos(x+\mathrm i y)\) is shown in figure at right in the \(x\), \(y\) plane with |
| − | levels |
+ | levels \(u=\Re(f)=\mathrm{const}\) and |
| − | levels |
+ | levels \(v=\Im(f)=\mathrm{const}\). |
Thick lines correspond to the Integer values. |
Thick lines correspond to the Integer values. |
||
The cut lines are shown with dashed lines. |
The cut lines are shown with dashed lines. |
||
==Symmetry== |
==Symmetry== |
||
| − | + | \(\arccos(-z)=\pi-\arccos(z)\) |
|
==Relation to other functions== |
==Relation to other functions== |
||
ArcCos can be expressed through function [[ArcSin]]: |
ArcCos can be expressed through function [[ArcSin]]: |
||
| − | : |
+ | :\( \displaystyle \arccos(z)=\frac{\pi}{2} - \arcsin(z)\) |
ArcCos can be expressed through functions [[Arccosh]]: |
ArcCos can be expressed through functions [[Arccosh]]: |
||
| − | : |
+ | : \(\displaystyle \arccos[z]=\frac{\pi}{2}- \mathrm i ~ \mathrm{arccosh}(\mathrm i \, z)\) |
==Behavior along the real axis== |
==Behavior along the real axis== |
||
| − | At the range |
+ | At the range \(-1\! \le \! x\le 1\), ArcCos is [[decreasing function]], it decreases from \(\pi\) to zero. |
Some specific values: |
Some specific values: |
||
| − | : |
+ | : \(\displaystyle \arccos\left( - \frac{\sqrt{3}}{2}\right)=\frac{5 \pi}{3}\) |
| − | : |
+ | : \(\displaystyle \arccos\left( - \frac{\sqrt{2}}{2}\right)=\frac{3 \pi}{4}\) |
| − | : |
+ | : \(\displaystyle \arccos\left(- \frac{1}{2}\right) ~=\frac{2\pi}{3}\) |
| − | : |
+ | : \(\displaystyle \arccos\left(~0 ~ \right) ~~ = ~\frac{\pi}{2}\) |
| − | : |
+ | : \(\displaystyle \arccos\left( \frac{1}{2}\right) ~ =\frac{\pi}{3}\) |
| − | : |
+ | : \(\displaystyle \arccos\left( \frac{\sqrt{2}}{2}\right)=\frac{ \pi}{4}\) |
| − | : |
+ | : \(\displaystyle \arccos\left( \frac{\sqrt{3}}{2}\right)=\frac{5 \pi}{3}\) |
Each of the values above can be used to construct the simple Taylor expansion, suitable for the approximations. Although the ArcCos of real argument is implemented in most of the programming language, the properties of such expansions are loaded to [[TORI]] as an example for treating of more complicated functions already required for the applicaitons; in particular, |
Each of the values above can be used to construct the simple Taylor expansion, suitable for the approximations. Although the ArcCos of real argument is implemented in most of the programming language, the properties of such expansions are loaded to [[TORI]] as an example for treating of more complicated functions already required for the applicaitons; in particular, |
||
for the efficient implementation of functions [[Sinc]], [[Cosc]] and their inverse functions [[ArcSinc]] and [[ArcCosc]], where |
for the efficient implementation of functions [[Sinc]], [[Cosc]] and their inverse functions [[ArcSinc]] and [[ArcCosc]], where |
||
| − | : |
+ | : \(\displaystyle \mathrm{sinc}(z)=\frac{\sin(z)}{z}~ ~ , ~ ~ \) (and zero if the argument is zero) |
| − | : |
+ | : \(\displaystyle \mathrm{cosc}(z)=\frac{\cos(z)}{z}\) |
==Numerical Implementation of acos== |
==Numerical Implementation of acos== |
||
| Line 72: | Line 72: | ||
Function [[Cos]] can be expanded at zero in the following way: |
Function [[Cos]] can be expanded at zero in the following way: |
||
| − | : |
+ | : \(\displaystyle \cos(t)=1-\frac{1}{2}t^2+\frac{1}{4!} t^4-\frac{1}{6!} t^6+ ..\) |
Then, |
Then, |
||
| − | : |
+ | : \(\displaystyle 1-\cos(t)=\frac{1}{2}t^2-\frac{1}{4!} t^4+\frac{1}{6!} t^6-\frac{1}{8!} t^8+ ..\) |
| − | Inversion of the series gives the expansion for ArcCos at the branch point |
+ | Inversion of the series gives the expansion for ArcCos at the branch point \(-1\): |
| − | : |
+ | : \(\displaystyle \arccos(1-t)= \sqrt{2t}+\frac{1}{6\sqrt{2}} t^{3/2}+\frac{3}{80\sqrt{2}} t^{5/2}+\frac{5}{448\sqrt{2}} t^{7/2}+ ..\) |
Similar expansion can be written for another branch point: |
Similar expansion can be written for another branch point: |
||
| − | : |
+ | : \(\displaystyle \arccos(-1+t)= \pi- \sqrt{2t}-\frac{1}{6\sqrt{2}} t^{3/2}-\frac{3}{80\sqrt{2}} t^{5/2}-\frac{5}{448\sqrt{2}} t^{7/2}+ ..\) |
The [[Radius of convergence]] of the two last series is equal to two; it is determined by the distance between the branch points. |
The [[Radius of convergence]] of the two last series is equal to two; it is determined by the distance between the branch points. |
||
[[Mathematica]] allows to calculate many terms of these expansions and evaluate them. In particular, |
[[Mathematica]] allows to calculate many terms of these expansions and evaluate them. In particular, |
||
| − | : |
+ | : \(\displaystyle \arccos(1- t)= \pi- \sqrt{t} \Big( |
| + | \) \( |
||
| − | $ $ |
||
| − | 1.4142135623730951 |
+ | 1.4142135623730951 \) \( |
| − | + 0.11785113019775792 t |
+ | + 0.11785113019775792 t \) \( |
| − | + 0.026516504294495532 t^2 |
+ | + 0.026516504294495532 t^2\) \( |
| − | + 0.007891816754314147 t^3 |
+ | + 0.007891816754314147 t^3\) \( |
| − | + 0.0026854098677874527 t^4 |
+ | + 0.0026854098677874527 t^4\) \( |
| − | + 0.0009887190876853803 t^5 |
+ | + 0.0009887190876853803 t^5\) \( |
| − | + 0.0003834455436215738 t^6 |
+ | + 0.0003834455436215738 t^6\) \( |
| − | + 0.0001542911830286809 t^7 |
+ | + 0.0001542911830286809 t^7\) \( |
+ 0.00006381528709825955 t^8 |
+ 0.00006381528709825955 t^8 |
||
| − | +.. \Big) |
+ | +.. \Big)\) |
==Keywords== |
==Keywords== |
||
Latest revision as of 18:47, 30 July 2019

ArcCos, or acos is holomorphic function, inverse of cos.
ArcCos is considered as elementary function
ArcCos, or acos, or arccos is holomorphic function, inverse of cos.
ArcCos is considered as elementary function
By definition, arccos is solution of equation
- \( \cos(\arccos(z))=z\)
Contents
Range of holomorphism
\(\arccos(z)\) is holomorphic in the whole complex plane except the halflines \(z\!\le\! -1\) and \(z\!\ge\! 1\).
Complex map or \(f=\arccos(x+\mathrm i y)\) is shown in figure at right in the \(x\), \(y\) plane with levels \(u=\Re(f)=\mathrm{const}\) and levels \(v=\Im(f)=\mathrm{const}\). Thick lines correspond to the Integer values. The cut lines are shown with dashed lines.
Symmetry
\(\arccos(-z)=\pi-\arccos(z)\)
Relation to other functions
ArcCos can be expressed through function ArcSin:
- \( \displaystyle \arccos(z)=\frac{\pi}{2} - \arcsin(z)\)
ArcCos can be expressed through functions Arccosh:
- \(\displaystyle \arccos[z]=\frac{\pi}{2}- \mathrm i ~ \mathrm{arccosh}(\mathrm i \, z)\)
Behavior along the real axis
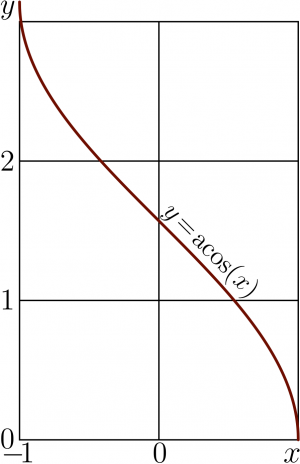
At the range \(-1\! \le \! x\le 1\), ArcCos is decreasing function, it decreases from \(\pi\) to zero.
Some specific values:
- \(\displaystyle \arccos\left( - \frac{\sqrt{3}}{2}\right)=\frac{5 \pi}{3}\)
- \(\displaystyle \arccos\left( - \frac{\sqrt{2}}{2}\right)=\frac{3 \pi}{4}\)
- \(\displaystyle \arccos\left(- \frac{1}{2}\right) ~=\frac{2\pi}{3}\)
- \(\displaystyle \arccos\left(~0 ~ \right) ~~ = ~\frac{\pi}{2}\)
- \(\displaystyle \arccos\left( \frac{1}{2}\right) ~ =\frac{\pi}{3}\)
- \(\displaystyle \arccos\left( \frac{\sqrt{2}}{2}\right)=\frac{ \pi}{4}\)
- \(\displaystyle \arccos\left( \frac{\sqrt{3}}{2}\right)=\frac{5 \pi}{3}\)
Each of the values above can be used to construct the simple Taylor expansion, suitable for the approximations. Although the ArcCos of real argument is implemented in most of the programming language, the properties of such expansions are loaded to TORI as an example for treating of more complicated functions already required for the applicaitons; in particular, for the efficient implementation of functions Sinc, Cosc and their inverse functions ArcSinc and ArcCosc, where
- \(\displaystyle \mathrm{sinc}(z)=\frac{\sin(z)}{z}~ ~ , ~ ~ \) (and zero if the argument is zero)
- \(\displaystyle \mathrm{cosc}(z)=\frac{\cos(z)}{z}\)
Numerical Implementation of acos
In some programing languages, acos is implemented only for real argument. However, it can be expressed through the log function as follows:
complex double acos(complex double z){
if(Im(z)<0){if(Re(z)>=0){return I*log( z + sqrt(z*z-1.) );}
else{return I*log( z - sqrt(z*z-1.) );}}
if(Re(z)>=0){return -I*log( z + sqrt(z*z-1.) );}
else {return -I*log( z - sqrt(z*z-1.) );} }
where I denotes the imaginary unity; Re and Im denote the real and imaginary parts. Fortunately, in the C++ compilers, function log is already implemented for complex double argument.
This implementation above used to plot the complex map of ArcCos at the top figure. In particular, the same representation can be used for real values of the argument; the explicit plot of ArcCos is generated with the same representation. (Click the figure to see the code used for its generation.) However, the last graphic could be generated also with the internal C++ function acos of real argument, as well as with flipping of plot of function cos.
Expansions of Cos and ArcCos
Expansion of ArcCos at the branch point
Function Cos can be expanded at zero in the following way:
- \(\displaystyle \cos(t)=1-\frac{1}{2}t^2+\frac{1}{4!} t^4-\frac{1}{6!} t^6+ ..\)
Then,
- \(\displaystyle 1-\cos(t)=\frac{1}{2}t^2-\frac{1}{4!} t^4+\frac{1}{6!} t^6-\frac{1}{8!} t^8+ ..\)
Inversion of the series gives the expansion for ArcCos at the branch point \(-1\):
- \(\displaystyle \arccos(1-t)= \sqrt{2t}+\frac{1}{6\sqrt{2}} t^{3/2}+\frac{3}{80\sqrt{2}} t^{5/2}+\frac{5}{448\sqrt{2}} t^{7/2}+ ..\)
Similar expansion can be written for another branch point:
- \(\displaystyle \arccos(-1+t)= \pi- \sqrt{2t}-\frac{1}{6\sqrt{2}} t^{3/2}-\frac{3}{80\sqrt{2}} t^{5/2}-\frac{5}{448\sqrt{2}} t^{7/2}+ ..\)
The Radius of convergence of the two last series is equal to two; it is determined by the distance between the branch points. Mathematica allows to calculate many terms of these expansions and evaluate them. In particular,
- \(\displaystyle \arccos(1- t)= \pi- \sqrt{t} \Big( \) \( 1.4142135623730951 \) \( + 0.11785113019775792 t \) \( + 0.026516504294495532 t^2\) \( + 0.007891816754314147 t^3\) \( + 0.0026854098677874527 t^4\) \( + 0.0009887190876853803 t^5\) \( + 0.0003834455436215738 t^6\) \( + 0.0001542911830286809 t^7\) \( + 0.00006381528709825955 t^8 +.. \Big)\)
Keywords
sin, cos, ArcSin, elementary function, inverse function, complex map, C++, Trigonometric functions