Difference between revisions of "ArcFactorial"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| Line 1: | Line 1: | ||
[[File:AfacmapT800.png|300px|right|thumb|map of ArcFactorial]] |
[[File:AfacmapT800.png|300px|right|thumb|map of ArcFactorial]] |
||
'''ArcFactorial''' is the principal branch of the inverse function of [[Factorial]]; |
'''ArcFactorial''' is the principal branch of the inverse function of [[Factorial]]; |
||
| − | : |
+ | : \( \mathrm{Factorial}(\mathrm{ArcFactorial}(z))=z\) |
| − | [[Complex map]] of |
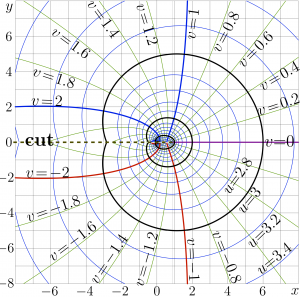
+ | [[Complex map]] of \(f=\mathrm{ArcFactorial}(x\!+\!\mathrm i y)\) is shown at right in the \(x\), \(y\) plane with |
| − | levels |
+ | levels \(u=\Re(f)=\mathrm {const}\) and levels |
| − | levels |
+ | levels \(v=\Im(f)=\mathrm {const}\). |
==Notations== |
==Notations== |
||
Also the notations |
Also the notations |
||
| − | : |
+ | : \(\mathrm{afac}=\mathrm{ArcFactorial}=\mathrm{Factorial}^{-1}\) |
are suggested. |
are suggested. |
||
| − | However, |
+ | However, \(\mathrm{Factorial}^{-1}(z)\) should not be confused with |
| − | : |
+ | : \(\displaystyle \mathrm{Factorial}(z)^{-1} = \frac{1}{\mathrm{Factorial}(z)}\) |
| − | and, in general, the |
+ | and, in general, the \(c\)th iteration of Factorial, id est, |
| − | : |
+ | : \(\mathrm{Factorial}^x(z)\) |
| − | should not be confused with the |
+ | should not be confused with the \(c\)th power of \(z!\), which is |
| − | : |
+ | : \(\mathrm{Factorial}(z)^c\) |
==Properties of ArcFactorial== |
==Properties of ArcFactorial== |
||
| − | ArcFactorial is holomorphic at the whole complex |
+ | ArcFactorial is holomorphic at the whole complex \(z\) plane except the half-line |
| − | : |
+ | : \(z\le \mathrm{Homer}\) |
where |
where |
||
| − | : |
+ | : \(\mathrm{Homer}=\mathrm{Factorial}(\mathrm{Bart})\approx 0.8856031944108887\) |
| − | and |
+ | and \(\mathrm{Bart}\approx 0.4616321449683622\) |
is solution of equation |
is solution of equation |
||
| − | : |
+ | : \(\mathrm{Factorial}'(\mathrm{Bart})=0\) |
Bart is the [[branchpoint]]; |
Bart is the [[branchpoint]]; |
||
| − | : |
+ | :\(\mathrm{ArcFactorial}(\mathrm{Homer})=\mathrm{Bart}\) |
At large values of argument, the ArcFactorial shows slow growth, similar to that of [[logarithm]]. |
At large values of argument, the ArcFactorial shows slow growth, similar to that of [[logarithm]]. |
||
==Real argument and special cases== |
==Real argument and special cases== |
||
| − | [[File:AfacplotT2px300.png|600px|right|thumb| |
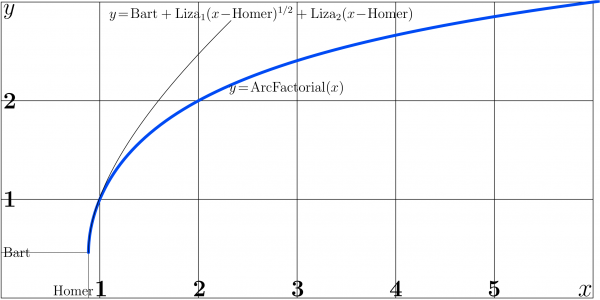
+ | [[File:AfacplotT2px300.png|600px|right|thumb|\(y=\mathrm{ArcFactorial}(x)\) and its asymptotic approximation]] |
Behavior of ArcFactorial along the real axis is shown in figure at right. |
Behavior of ArcFactorial along the real axis is shown in figure at right. |
||
For some [[natural number|natural]] values of argument, ArcFactorial has natural values: |
For some [[natural number|natural]] values of argument, ArcFactorial has natural values: |
||
| − | : |
+ | : \(\mathrm{ArcFactorial}(1)=1\) |
| − | : |
+ | : \(\mathrm{ArcFactorial}(2)=2\) |
| − | : |
+ | : \(\mathrm{ArcFactorial}(6)=3\) |
| − | : |
+ | : \(\mathrm{ArcFactorial}(24)\!=4\) |
and so on. |
and so on. |
||
At certain specific values of argument, ArcFactorial has half-integer values: |
At certain specific values of argument, ArcFactorial has half-integer values: |
||
| − | : |
+ | : \(\displaystyle \mathrm{ArcFactorial}\left( \frac{\sqrt{\pi}}{2}\right)\!=\frac{1}{2}\) |
| − | : |
+ | : \(\displaystyle \mathrm{ArcFactorial}\left( \frac{3\sqrt{\pi}}{4}\right)\!=\frac{3}{2}\) |
| − | : |
+ | : \(\displaystyle \mathrm{ArcFactorial}\left( \frac{15\sqrt{\pi}}{8}\right)\!=\frac{5}{2}\) |
==Expansion at Homer== |
==Expansion at Homer== |
||
The expansion of [[Factorial]] at its minimum has form |
The expansion of [[Factorial]] at its minimum has form |
||
| − | : |
+ | : \(\mathrm{Factorial}(\mathrm{Bart}+t)=\mathrm{Homer} |
+\frac{1}{2}\mathrm{Factorial''}(\mathrm{Bart}) t^2 |
+\frac{1}{2}\mathrm{Factorial''}(\mathrm{Bart}) t^2 |
||
| − | +\frac{1}{6}\mathrm{Factorial'''}(\mathrm{Bart}) t^3+ .. |
+ | +\frac{1}{6}\mathrm{Factorial'''}(\mathrm{Bart}) t^3+ .. \) |
The [[InverseSeries]] gives the expansion for the ArcFactorial: |
The [[InverseSeries]] gives the expansion for the ArcFactorial: |
||
| − | : |
+ | : \(\mathrm{ArcFactorial}(\mathrm{Homer}+t)=\mathrm{Bart} |
+ \mathrm{Liza}_1 t^{1/2} |
+ \mathrm{Liza}_1 t^{1/2} |
||
+ \mathrm{Liza}_2 t |
+ \mathrm{Liza}_2 t |
||
| − | + \mathrm{Liza}_3 t^{3/2}+ ... |
+ | + \mathrm{Liza}_3 t^{3/2}+ ...\) |
where |
where |
||
| − | : |
+ | : \(\mathrm{Liza}_1 =\sqrt{\frac{2}{\mathrm{Factorial}''(\mathrm{Bart})}} \approx ~ 1.5276760433847776\) |
| − | : |
+ | : \(\mathrm{Liza}_2 \approx ~ 0.3559463008501492\) |
| − | : |
+ | : \(\mathrm{Liza}_3 \approx \! -0.4620189870305121\) |
| − | : |
+ | : \(\mathrm{Liza}_4 \approx \! -0.19468729558612438 \) |
==References== |
==References== |
||
Latest revision as of 18:26, 30 July 2019
ArcFactorial is the principal branch of the inverse function of Factorial;
- \( \mathrm{Factorial}(\mathrm{ArcFactorial}(z))=z\)
Complex map of \(f=\mathrm{ArcFactorial}(x\!+\!\mathrm i y)\) is shown at right in the \(x\), \(y\) plane with levels \(u=\Re(f)=\mathrm {const}\) and levels levels \(v=\Im(f)=\mathrm {const}\).
Contents
Notations
Also the notations
- \(\mathrm{afac}=\mathrm{ArcFactorial}=\mathrm{Factorial}^{-1}\)
are suggested.
However, \(\mathrm{Factorial}^{-1}(z)\) should not be confused with
- \(\displaystyle \mathrm{Factorial}(z)^{-1} = \frac{1}{\mathrm{Factorial}(z)}\)
and, in general, the \(c\)th iteration of Factorial, id est,
- \(\mathrm{Factorial}^x(z)\)
should not be confused with the \(c\)th power of \(z!\), which is
- \(\mathrm{Factorial}(z)^c\)
Properties of ArcFactorial
ArcFactorial is holomorphic at the whole complex \(z\) plane except the half-line
- \(z\le \mathrm{Homer}\)
where
- \(\mathrm{Homer}=\mathrm{Factorial}(\mathrm{Bart})\approx 0.8856031944108887\)
and \(\mathrm{Bart}\approx 0.4616321449683622\) is solution of equation
- \(\mathrm{Factorial}'(\mathrm{Bart})=0\)
Bart is the branchpoint;
- \(\mathrm{ArcFactorial}(\mathrm{Homer})=\mathrm{Bart}\)
At large values of argument, the ArcFactorial shows slow growth, similar to that of logarithm.
Real argument and special cases
Behavior of ArcFactorial along the real axis is shown in figure at right.
For some natural values of argument, ArcFactorial has natural values:
- \(\mathrm{ArcFactorial}(1)=1\)
- \(\mathrm{ArcFactorial}(2)=2\)
- \(\mathrm{ArcFactorial}(6)=3\)
- \(\mathrm{ArcFactorial}(24)\!=4\)
and so on.
At certain specific values of argument, ArcFactorial has half-integer values:
- \(\displaystyle \mathrm{ArcFactorial}\left( \frac{\sqrt{\pi}}{2}\right)\!=\frac{1}{2}\)
- \(\displaystyle \mathrm{ArcFactorial}\left( \frac{3\sqrt{\pi}}{4}\right)\!=\frac{3}{2}\)
- \(\displaystyle \mathrm{ArcFactorial}\left( \frac{15\sqrt{\pi}}{8}\right)\!=\frac{5}{2}\)
Expansion at Homer
The expansion of Factorial at its minimum has form
- \(\mathrm{Factorial}(\mathrm{Bart}+t)=\mathrm{Homer} +\frac{1}{2}\mathrm{Factorial''}(\mathrm{Bart}) t^2 +\frac{1}{6}\mathrm{Factorial'''}(\mathrm{Bart}) t^3+ .. \)
The InverseSeries gives the expansion for the ArcFactorial:
- \(\mathrm{ArcFactorial}(\mathrm{Homer}+t)=\mathrm{Bart} + \mathrm{Liza}_1 t^{1/2} + \mathrm{Liza}_2 t + \mathrm{Liza}_3 t^{3/2}+ ...\)
where
- \(\mathrm{Liza}_1 =\sqrt{\frac{2}{\mathrm{Factorial}''(\mathrm{Bart})}} \approx ~ 1.5276760433847776\)
- \(\mathrm{Liza}_2 \approx ~ 0.3559463008501492\)
- \(\mathrm{Liza}_3 \approx \! -0.4620189870305121\)
- \(\mathrm{Liza}_4 \approx \! -0.19468729558612438 \)
References