Difference between revisions of "ArcTetration"
(→Application) |
|||
| (17 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <div style="float:right; width:320px"> |
||
| − | #redirect[[ArcTetration]] |
||
| + | [[File:Ater01.png|340px]] |
||
| + | \( \mathrm{ate}_b(x) \) versus \( x \) for various \(b\) |
||
| + | |||
| + | [[File:B271a.png|340px]] |
||
| + | [[Complex map]]: \( u\!+ \!\mathrm i v \!=\! \mathrm{ate}_b(x\!+\!\mathrm i y)~\) at \( b\!=\!\mathrm e \) |
||
| + | </div> |
||
| + | [[ArcTetration]] \( \mathrm{ate} \) is inverse function of [[tetration]] |
||
| + | <ref> |
||
| + | http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html |
||
| + | http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf |
||
| + | D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation 78 (2009), 1647-1670. |
||
| + | </ref>. |
||
| + | |||
| + | [[ArcTetration]] is [[Abel function]] of the [[exponential]]. |
||
| + | |||
| + | ==Basic properties of ArcTetration== |
||
| + | For real values of the argument, |
||
| + | \( \mathrm{ate}_b(x) \) is plotted versus \( x \) at various valies of \( b\!>\!1 \). |
||
| + | Being the inverse function of [[tetration]], the ArcTetration \( \mathrm {ate}_b \) to base \( b \) satisfies the relations |
||
| + | : \( \mathrm{ate}_b(\mathrm{tet}_b(z))=z \) |
||
| + | : \( \mathrm{tet}_b(\mathrm{ate}_b(z))=z \) |
||
| + | at least in some ranges of values of \( z \). |
||
| + | |||
| + | The ArcTetration satisfies the [[Abel equation]] |
||
| + | : \( \mathrm{ate}_b(b^z)=\mathrm{ate}_b(z) +1 \) |
||
| + | for the [[exponential]] as the [[transfer function]]. In this sense, ArcTetration is an [[Abel function]] of the exponential. |
||
| + | Roughly, the arctetration counts, how many times the logarithm should be taken of a value before the value becomes unity. |
||
| + | |||
| + | For base \( b\!=\!\mathrm e \!\approx\! 2.71 \), the natural ArcTetration is presented in figure at right with the [[complex map]]. For \( f\!=\!\mathrm{ate}(x+\mathrm i y) \), the isolines |
||
| + | \( u\!=\!\Re(f) \) and |
||
| + | \( v\!=\!\Im(f) \) are drawn in the \(x \), \(y \) plane. |
||
| + | |||
| + | ==Terminology and cuts== |
||
| + | In some publications, the term [[super-logarithm]] is used instead of [[ArcTetration]]. |
||
| + | |||
| + | Such a notation may cause confusion, because [[ArcTetration]] is not a [[superfunction]] of [[logarithm]]. |
||
| + | For this reason, in [[TORI]] the name ArcTetration is used. |
||
| + | |||
| + | According to the definition of [[Abel function]], ArcTetration is Abel function of the exponential. However, the additional requirement that |
||
| + | \( \mathrm{tet}_b(\mathrm{ate}_b(z))\!=\!z~\) at least in some vicinity of the [[real axis]] specifies that |
||
| + | :\(\mathrm{ate}_b(1)=0\) |
||
| + | and determines its asymptotic properties; in particular, its behavior in vicinity of the fixed points of the exponential, which are the [[branch point]]s of \( \mathrm{ate}_b \). The cut line(s) for ArcTetrational are chosen to be "horisontal" (assuming that the complex plane at the screen is vertical), they go from a fixed point of exponential to the left, to the negative values of the real part of the argument, keeping the imaginary part. In particular, for \( 1\!<\!b\!<\!\exp(1/\mathrm e) \), the fixed points of \( \exp_b \) are real, and the ArcTetration \( \mathrm{ate}_b \) has the only one cut line, that goes to \( -\infty \) along the real axis. |
||
| + | |||
| + | <!-- |
||
| + | While the tetration is [[superfunction]] of the [[exponential]], the arctetration is the [[Abel function]]. |
||
| + | !--> |
||
| + | ==Uniqueness of ArcTetration== |
||
| + | The requirement on the behavior of ArcTetration as the argument approaches the [[fixed point]]s of the corresponding exponential provide the uniqueness of this function. |
||
| + | |||
| + | For \( b\!>\!\exp(1/\mathrm e) \), the conditions of the uniqueness are determined by the requirement of bi-holomorphism in certain range that extends from one fixed point of the exponential to another fixed point |
||
| + | <ref name="uniabel"> |
||
| + | http://www.springerlink.com/content/u7327836m2850246/<br> |
||
| + | http://mizugadro.mydns.jp/PAPERS/2011uniabel.pdf |
||
| + | H.Trappmann, D.Kouznetsov. Uniqueness of Analytic Abel Functions in Absence of a Real Fixed Point. [[Aequationes Mathematicae]], v.81, p.65-76 (2011) |
||
| + | </ref>. |
||
| + | |||
| + | ==Numerical evaluation== |
||
| + | For real base \( b\!>\!1 \), the ArcTetration can be evaluated with numerical inversion of [[tetration]]. |
||
| + | For \( b=\mathrm e\), which refers to the "natural tetration", the 14-digit complex(double) [[C++]] implementation is available |
||
| + | <ref name="vladie"> |
||
| + | http://mizugadro.mydns.jp/PAPERS/2010vladie.pdf |
||
| + | D.Kouznetsov. Superexponential as special function. [[Vladikavkaz Mathematical Journal]], 2010, v.12, issue 2, p.31-45. |
||
| + | </ref>. |
||
| + | |||
| + | ==Application== |
||
| + | <div class="thumb tright" style="float:right;width:230px"> |
||
| + | [[File:Qexpmap.jpg|250px]] |
||
| + | [[Complex map]] |
||
| + | \( p\!+\!\mathrm{i} q=\varphi(x\!+\!\mathrm{i} y) \) |
||
| + | <ref name="f"> |
||
| + | http://www.ils.uec.ac.jp/~dima/PAPERS/2009supefae.pdf <br> |
||
| + | http://mizugadro.mydns.jp/PAPERS/2010superfae.pdf <br> |
||
| + | http://mizugadro.mydns.jp/PAPERS/2010superfar.pdf <br> |
||
| + | D.Kouznetsov, H.Trappmann. Superfunctions and sqrt of Factorial. |
||
| + | SSN 00271349, Moscow University Physics Bulletin, 2010, Vol. 65, No. 1, pp. 6–12. © Allerton Press, Inc., 2010. Published in Russian in Vestnik Moskovskogo Universiteta. Fizika, 2010, No. 1, pp. 8–14. |
||
| + | Abstract — The holomorphic function h is constructed such that h(h(z))=z! ; this function is interpreted as square root of Factorial. |
||
| + | </ref> |
||
| + | </div> |
||
| + | Together with [[tetration]] \( \mathrm{tet} \), the [[ArcTetration]] determines the [[iterate|fractional iteration]] of the exponential. The \( n \)th iteration of \( \exp_b \) is defined as follows: |
||
| + | :\( {\exp_b}^n = \mathrm {tet}_b( n + \mathrm{ate}_b(z)) \) |
||
| + | At \( 0\!<\!n\!<\!1 \), such a function may be useful for description of processes that grow faster than any polynomial but slower than any exponential. Such functions greatly extend the ability of holomorphic fitting of dependences with non-trivial (or just unknown) asymptotic behavior. |
||
| + | |||
| + | In particular, function \( \varphi \) mentioned in the title of publication by [[Hellmuth Kneser]] |
||
| + | <ref name="k"> |
||
| + | http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002175851&physid=phys63#navi |
||
| + | [[Hellmuth Kneser]]. Reelle analytische Lösungen der Gleichung \( \varphi(\varphi(x))=\mathrm e^x \) und verwandter Funktionalgleichungen. |
||
| + | Journal für die reine und angewandte Mathematik / Zeitschriftenband (1950) / Artikel / 56 - 67 |
||
| + | </ref> |
||
| + | is just iteration half of the exponential, [[square root of exponential]], \( \sqrt{\exp} \); |
||
| + | it corresponds to the formula above at \( n=1/2 \) and \( b=\mathrm e=\exp(1)\approx 2.71 \). |
||
| + | |||
| + | It is solution of equation \( \varphi(\varphi(z))=\exp(z) \) |
||
| + | |||
| + | [[Complex map]] of this function is shown in figure at right in the palane \( z\!=\! z\!+\!\mathrm i y \) with <br> |
||
| + | lines \( p=\Re(\varphi(z)) = \mathrm{const} \) and <br> |
||
| + | lines \( q=\Im(\varphi(z)) = \mathrm{const} \). |
||
| + | |||
| + | Also, the ArcTetration can be used for the numerical representation of huge numbers, that cannot be stored in the conventional floating-point form (mantissa, logarithm). Instead of to store a huge number \( N\), one may store just \(\mathrm{ate}(N)\). Due to the fast growth of [[tetration]], such a representation is not precise at all, but it greatly extends the range of real numbers that are still distinguishable from infinity. However, the arithmetical functions should be implemented in such a way, that no conversion of the number into the conventional (floating point) form is required at the intermediate steps. |
||
| + | |||
| + | ==[[Superfunctions]]== |
||
| + | |||
| + | [[ArcTetration]] ate is described in book [[Superfunctions]] |
||
| + | <ref> |
||
| + | http://mizugadro.mydns.jp/BOOK/444.pdf |
||
| + | Dmitrii Kouznetsov. Superfunctions. 2015-2019. |
||
| + | </ref> |
||
| + | |||
| + | ==References== |
||
| + | <references/> |
||
| + | |||
| + | |||
| + | ==Keywords== |
||
| + | [[Abel equation]], |
||
| + | [[Abel function]], |
||
| + | [[Hellmuth Kneser]], |
||
| + | [[Superfunction]], |
||
| + | [[Superfunctions]], |
||
| + | [[Transfer equation]], |
||
| + | [[Transfer function]] |
||
| + | |||
| + | [[Category:Abelfunction]] |
||
| + | [[Category:Superfunction]] |
||
| + | [[Category:Superfunctions]] |
||
| + | [[Category:Tetration]] |
||
| + | [[Category:Hellmuth Kneser]] |
||
| + | [[Category:Holomorphic function]] |
||
| + | [[Category:Articles in English]] |
||
Latest revision as of 23:03, 30 November 2019
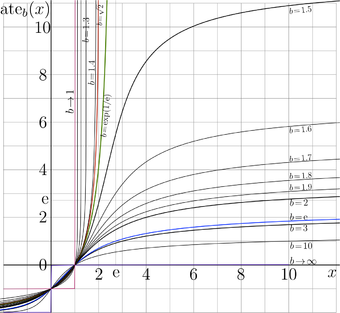 \( \mathrm{ate}_b(x) \) versus \( x \) for various \(b\)
\( \mathrm{ate}_b(x) \) versus \( x \) for various \(b\)
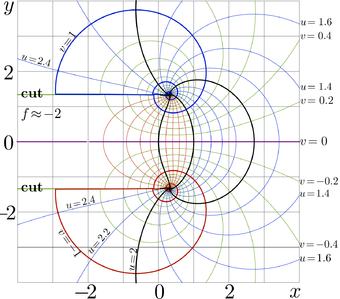 Complex map: \( u\!+ \!\mathrm i v \!=\! \mathrm{ate}_b(x\!+\!\mathrm i y)~\) at \( b\!=\!\mathrm e \)
Complex map: \( u\!+ \!\mathrm i v \!=\! \mathrm{ate}_b(x\!+\!\mathrm i y)~\) at \( b\!=\!\mathrm e \)
ArcTetration \( \mathrm{ate} \) is inverse function of tetration [1].
ArcTetration is Abel function of the exponential.
Contents
Basic properties of ArcTetration
For real values of the argument, \( \mathrm{ate}_b(x) \) is plotted versus \( x \) at various valies of \( b\!>\!1 \). Being the inverse function of tetration, the ArcTetration \( \mathrm {ate}_b \) to base \( b \) satisfies the relations
- \( \mathrm{ate}_b(\mathrm{tet}_b(z))=z \)
- \( \mathrm{tet}_b(\mathrm{ate}_b(z))=z \)
at least in some ranges of values of \( z \).
The ArcTetration satisfies the Abel equation
- \( \mathrm{ate}_b(b^z)=\mathrm{ate}_b(z) +1 \)
for the exponential as the transfer function. In this sense, ArcTetration is an Abel function of the exponential. Roughly, the arctetration counts, how many times the logarithm should be taken of a value before the value becomes unity.
For base \( b\!=\!\mathrm e \!\approx\! 2.71 \), the natural ArcTetration is presented in figure at right with the complex map. For \( f\!=\!\mathrm{ate}(x+\mathrm i y) \), the isolines \( u\!=\!\Re(f) \) and \( v\!=\!\Im(f) \) are drawn in the \(x \), \(y \) plane.
Terminology and cuts
In some publications, the term super-logarithm is used instead of ArcTetration.
Such a notation may cause confusion, because ArcTetration is not a superfunction of logarithm. For this reason, in TORI the name ArcTetration is used.
According to the definition of Abel function, ArcTetration is Abel function of the exponential. However, the additional requirement that \( \mathrm{tet}_b(\mathrm{ate}_b(z))\!=\!z~\) at least in some vicinity of the real axis specifies that
- \(\mathrm{ate}_b(1)=0\)
and determines its asymptotic properties; in particular, its behavior in vicinity of the fixed points of the exponential, which are the branch points of \( \mathrm{ate}_b \). The cut line(s) for ArcTetrational are chosen to be "horisontal" (assuming that the complex plane at the screen is vertical), they go from a fixed point of exponential to the left, to the negative values of the real part of the argument, keeping the imaginary part. In particular, for \( 1\!<\!b\!<\!\exp(1/\mathrm e) \), the fixed points of \( \exp_b \) are real, and the ArcTetration \( \mathrm{ate}_b \) has the only one cut line, that goes to \( -\infty \) along the real axis.
Uniqueness of ArcTetration
The requirement on the behavior of ArcTetration as the argument approaches the fixed points of the corresponding exponential provide the uniqueness of this function.
For \( b\!>\!\exp(1/\mathrm e) \), the conditions of the uniqueness are determined by the requirement of bi-holomorphism in certain range that extends from one fixed point of the exponential to another fixed point [2].
Numerical evaluation
For real base \( b\!>\!1 \), the ArcTetration can be evaluated with numerical inversion of tetration. For \( b=\mathrm e\), which refers to the "natural tetration", the 14-digit complex(double) C++ implementation is available [3].
Application
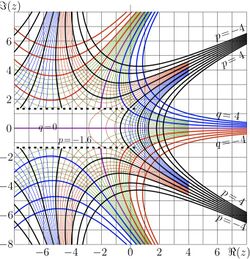 Complex map
\( p\!+\!\mathrm{i} q=\varphi(x\!+\!\mathrm{i} y) \)
[4]
Complex map
\( p\!+\!\mathrm{i} q=\varphi(x\!+\!\mathrm{i} y) \)
[4]
Together with tetration \( \mathrm{tet} \), the ArcTetration determines the fractional iteration of the exponential. The \( n \)th iteration of \( \exp_b \) is defined as follows:
- \( {\exp_b}^n = \mathrm {tet}_b( n + \mathrm{ate}_b(z)) \)
At \( 0\!<\!n\!<\!1 \), such a function may be useful for description of processes that grow faster than any polynomial but slower than any exponential. Such functions greatly extend the ability of holomorphic fitting of dependences with non-trivial (or just unknown) asymptotic behavior.
In particular, function \( \varphi \) mentioned in the title of publication by Hellmuth Kneser [5] is just iteration half of the exponential, square root of exponential, \( \sqrt{\exp} \); it corresponds to the formula above at \( n=1/2 \) and \( b=\mathrm e=\exp(1)\approx 2.71 \).
It is solution of equation \( \varphi(\varphi(z))=\exp(z) \)
Complex map of this function is shown in figure at right in the palane \( z\!=\! z\!+\!\mathrm i y \) with
lines \( p=\Re(\varphi(z)) = \mathrm{const} \) and
lines \( q=\Im(\varphi(z)) = \mathrm{const} \).
Also, the ArcTetration can be used for the numerical representation of huge numbers, that cannot be stored in the conventional floating-point form (mantissa, logarithm). Instead of to store a huge number \( N\), one may store just \(\mathrm{ate}(N)\). Due to the fast growth of tetration, such a representation is not precise at all, but it greatly extends the range of real numbers that are still distinguishable from infinity. However, the arithmetical functions should be implemented in such a way, that no conversion of the number into the conventional (floating point) form is required at the intermediate steps.
Superfunctions
ArcTetration ate is described in book Superfunctions [6]
References
- ↑ http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation 78 (2009), 1647-1670.
- ↑
http://www.springerlink.com/content/u7327836m2850246/
http://mizugadro.mydns.jp/PAPERS/2011uniabel.pdf H.Trappmann, D.Kouznetsov. Uniqueness of Analytic Abel Functions in Absence of a Real Fixed Point. Aequationes Mathematicae, v.81, p.65-76 (2011) - ↑ http://mizugadro.mydns.jp/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45.
- ↑
http://www.ils.uec.ac.jp/~dima/PAPERS/2009supefae.pdf
http://mizugadro.mydns.jp/PAPERS/2010superfae.pdf
http://mizugadro.mydns.jp/PAPERS/2010superfar.pdf
D.Kouznetsov, H.Trappmann. Superfunctions and sqrt of Factorial. SSN 00271349, Moscow University Physics Bulletin, 2010, Vol. 65, No. 1, pp. 6–12. © Allerton Press, Inc., 2010. Published in Russian in Vestnik Moskovskogo Universiteta. Fizika, 2010, No. 1, pp. 8–14. Abstract — The holomorphic function h is constructed such that h(h(z))=z! ; this function is interpreted as square root of Factorial. - ↑ http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002175851&physid=phys63#navi Hellmuth Kneser. Reelle analytische Lösungen der Gleichung \( \varphi(\varphi(x))=\mathrm e^x \) und verwandter Funktionalgleichungen. Journal für die reine und angewandte Mathematik / Zeitschriftenband (1950) / Artikel / 56 - 67
- ↑ http://mizugadro.mydns.jp/BOOK/444.pdf Dmitrii Kouznetsov. Superfunctions. 2015-2019.
Keywords
Abel equation, Abel function, Hellmuth Kneser, Superfunction, Superfunctions, Transfer equation, Transfer function