Difference between revisions of "ArkNem"

From TORI
Jump to: navigation, search
 
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)")
 
Line 1: Line 1:
−
[[File:Arknem1nap.jpg|400px|thumb||$u\!+\!\mathrm i v=\mathrm{ArkNem}_1(x\!+\!\mathrm i y)$]]
 +
[[File:Arknem1nap.jpg|400px|thumb||\(u\!+\!\mathrm i v=\mathrm{ArkNem}_1(x\!+\!\mathrm i y)\)]]
−
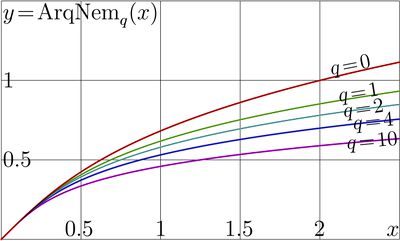
[[File:Arqnemplot.jpg|400px|thumb|$y\!=\!\mathrm{ArkNem}_{q}(x)$ versus $x$ for various $q$]]
 +
[[File:Arqnemplot.jpg|400px|thumb|\(y\!=\!\mathrm{ArkNem}_{q}(x)\) versus \(x\) for various \(q\)]]
   
   
 
[[ArcNem]] is one of inverse functions of the [[Nemtsov function]],
  
[[ArcNem]] is one of inverse functions of the [[Nemtsov function]],
   
−
$\mathrm{Nem}_q(z)=z+z^3+qz^4$
 +
\(\mathrm{Nem}_q(z)=z+z^3+qz^4\)
   
−
where $q$ is positive parameter. It can be indicated as subscript.
 +
where \(q\) is positive parameter. It can be indicated as subscript.
   
−
[[ArkNem]] is characterises with positions of the cut lines; they go from the branch points to $\mathrm i \infty$ horizontally to $-\infty$, parallel to the real axis.
 +
[[ArkNem]] is characterises with positions of the cut lines; they go from the branch points to \(\mathrm i \infty\) horizontally to \(-\infty\), parallel to the real axis.
   
−
For case $q\!=\!1$, the complex map of function ArcNem is shown in figure.
 +
For case \(q\!=\!1\), the complex map of function ArcNem is shown in figure.
   
 
==Description==
  
==Description==
Line 30: Line 30:
 
each of them happen to be better than its precedent in the sense of range of holomorphism of the resulting abelfunction. The last one, [[ArqNem]], is used for the implementation of function [[AuNem]].
  
each of them happen to be better than its precedent in the sense of range of holomorphism of the resulting abelfunction. The last one, [[ArqNem]], is used for the implementation of function [[AuNem]].
   
−
For positive values $x$ of the argument, these four functions coincide:
 +
For positive values \(x\) of the argument, these four functions coincide:
   
−
[[ArcNem]]$_q(x)=$
 +
[[ArcNem]]\(_q(x)=\)
−
[[Ar3Nem]]$_q(x)=$
 +
[[Ar3Nem]]\(_q(x)=\)
−
[[ArkNem]]$_q(x)=$
 +
[[ArkNem]]\(_q(x)=\)
−
[[ArqNem]]$_q(x)$
 +
[[ArqNem]]\(_q(x)\)
   
−
Explicit plot of this function is shown in figure for various values of $q$.
 +
Explicit plot of this function is shown in figure for various values of \(q\).
   
−
Function [[ArkNem]]$_q(z)$ has 3 branchponts. one of them is at the negative part of the real axis; two other are
+
Function [[ArkNem]]\(_q(z)\) has 3 branchponts. one of them is at the negative part of the real axis; two other are
 
expressed through function [[NemBran]]:
  
expressed through function [[NemBran]]:
   
−
$z=\pm $ [[NemBran]]$(q)$
 +
\(z=\pm \) [[NemBran]]\((q)\)
   
−
From these two points, at the complex plane, the cut lines go vertically to $\pm \mathrm i \infty$.
 +
From these two points, at the complex plane, the cut lines go vertically to \(\pm \mathrm i \infty\).
−
These cut lines divide the complex plane to two part, connected only by "bridge" between points $\pm $ [[NemBran]]$(q)$
 +
These cut lines divide the complex plane to two part, connected only by "bridge" between points \(\pm \) [[NemBran]]\((q)\)
   
 
This behaviour is not so good for testing of the implementation of iterates of the Nemtsov function;
  
This behaviour is not so good for testing of the implementation of iterates of the Nemtsov function;
Line 52: Line 52:
   
 
==[[C++]] implementation==
  
==[[C++]] implementation==
−
// The code below uses the routine [[nembran.cin]] to evaluate the branch point [[NemBran]] of the [[ArcNem]] at given value of parameter $q$.
 +
// The code below uses the routine [[nembran.cin]] to evaluate the branch point [[NemBran]] of the [[ArcNem]] at given value of parameter \(q\).
 
Value or the branch point is stored in global variables tr, ti.
  
Value or the branch point is stored in global variables tr, ti.
   
Line 62: Line 62:
 
arnemR,
  
arnemR,
 
arnemL;
  
arnemL;
−
they differ only in the way variable $H$ is expressed through variable $h$ and variable $R$ is expressed through variable $r$
 +
they differ only in the way variable \(H\) is expressed through variable \(h\) and variable \(R\) is expressed through variable \(r\)
   
−
$H=\sqrt{h}$, $H=-\sqrt{h}$, $H=\mathrm i \sqrt{-h}$, or $H=-\mathrm i \sqrt{-h}$, and
 +
\(H=\sqrt{h}\), \(H=-\sqrt{h}\), \(H=\mathrm i \sqrt{-h}\), or \(H=-\mathrm i \sqrt{-h}\), and
 
the same about relation between variables R,r and G,g;
  
the same about relation between variables R,r and G,g;
 
dependently on value of the argument, the coresponding branch of function [[sqrt]] is used, in order to provide the desirable position of the cut lines. */
  
dependently on value of the argument, the coresponding branch of function [[sqrt]] is used, in order to provide the desirable position of the cut lines. */

Latest revision as of 18:47, 30 July 2019

File:Arknem1nap.jpg
\(u\!+\!\mathrm i v=\mathrm{ArkNem}_1(x\!+\!\mathrm i y)\)
\(y\!=\!\mathrm{ArkNem}_{q}(x)\) versus \(x\) for various \(q\)


ArcNem is one of inverse functions of the Nemtsov function,

\(\mathrm{Nem}_q(z)=z+z^3+qz^4\)

where \(q\) is positive parameter. It can be indicated as subscript.

ArkNem is characterises with positions of the cut lines; they go from the branch points to \(\mathrm i \infty\) horizontally to \(-\infty\), parallel to the real axis.

For case \(q\!=\!1\), the complex map of function ArcNem is shown in figure.

Description

Function ArkNem is implemented in order to extend the range of holomorphism of the abelfunction Nemtsov function.

The naive inverse function, that grows from zero to infinity along the positive part of the real axis can be generated tithe mathematica code

Solve[ f+f^3+q f^4=z, f]

This code returns 4 solutions. The 3d solution is denoted with Ar3Nem. It grows from zero to infinity along the positive part of the real axis, following the intuitive expectation about it. However, the cut lines limit the range of holomorphism of the resulting abelfunction.

So, the 3 modifications are implemented: ArcNem, ArkNem and ArqNem.

each of them happen to be better than its precedent in the sense of range of holomorphism of the resulting abelfunction. The last one, ArqNem, is used for the implementation of function AuNem.

For positive values \(x\) of the argument, these four functions coincide:

ArcNem\(_q(x)=\) Ar3Nem\(_q(x)=\) ArkNem\(_q(x)=\) ArqNem\(_q(x)\)

Explicit plot of this function is shown in figure for various values of \(q\).

Function ArkNem\(_q(z)\) has 3 branchponts. one of them is at the negative part of the real axis; two other are expressed through function NemBran:

\(z=\pm \) NemBran\((q)\)

From these two points, at the complex plane, the cut lines go vertically to \(\pm \mathrm i \infty\). These cut lines divide the complex plane to two part, connected only by "bridge" between points \(\pm \) NemBran\((q)\)

This behaviour is not so good for testing of the implementation of iterates of the Nemtsov function; so, functions ArkNem and ArqNem are also implemanated.

C++ implementation

// The code below uses the routine nembran.cin to evaluate the branch point NemBran of the ArcNem at given value of parameter \(q\). Value or the branch point is stored in global variables tr, ti.

/* Function ArkNem above is evaluated by one of very similar routines, arnemU, arnemD, arnemR, arnemL; they differ only in the way variable \(H\) is expressed through variable \(h\) and variable \(R\) is expressed through variable \(r\)

\(H=\sqrt{h}\), \(H=-\sqrt{h}\), \(H=\mathrm i \sqrt{-h}\), or \(H=-\mathrm i \sqrt{-h}\), and the same about relation between variables R,r and G,g; dependently on value of the argument, the coresponding branch of function sqrt is used, in order to provide the desirable position of the cut lines. */

References


Keywords

Ar3Nem, ArcNem, ArkNem, ArqNem, Branch point, Cut line, Inverse function, Nemtsov function

Retrieved from "https://mizugadro.mydns.jp/t/index.php?title=ArkNem&oldid=28416"