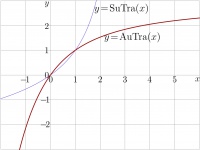
AuTra
AuTra is the inverse function of SuTra.
AuTra is Abel function of the Trappmann function, $\mathrm{tra}(z)=z+\exp(z)$.
AuTra satisfies the Abel equation
$ \mathrm{AuTra} \Big( \mathrm{tra}(z) \Big)= \mathrm{AuTra}(z)+1$
and the additional condition
$ \mathrm{AuTra}(1)=0~$ .
This condition corresponds to relation $~\mathrm{SuTra}(0)=1~$. The same choice of the initial value is used also for many other superfunctions, including tetration, SuZex function, Tania function and Shoka function.
AuTra is real-holomorphic, $\mathrm{AuTra}(z^*)=\mathrm{AuTra}(z)^*$
Contents
Branch points, cut lines and growth
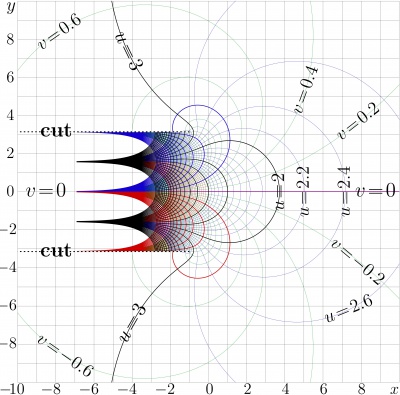
AuTra has two branch points $~B_{\pm}=-1\! \pm\!\mathrm i \pi ~$;
$\mathrm{Au}_{\pm} := \mathrm{AuTra}(B_{\pm}) \approx 3.4101257504807645 \pm 1.4101841452081931 \, \mathrm i$
These branch points corresponds to the zero derivative of function SuTra;
$\mathrm{SuTra}(\mathrm{Au}_{\pm}) = -1\! \pm\!\mathrm i \pi ~$
$\mathrm{SuTra}^\prime (\mathrm{Au}_{\pm}) =0 ~$
The cut lines
$\{ z\in \mathbb C : ~ \Im(z)\!=\!\pm i, ~ \Re(z)\le -1 \}$
are directed to the left hand side of the complex plane, parallel to the real axis. In TORI, this is default choice of the cut lines.
Between the cut llines, AuTra grows exponentially in the direction of decrease of the real part of the argument.
Outside the cut lines, AuTra]] grows slowly, similarly to the ArcTetration. In particular, AuTra shows this slow growth along the positive direction of the real axis. This growth is a little bit faster than that of function AuZex:
$\mathrm{AuTraM}(z)=\mathrm{AuZex}( \mathrm e^z )$
Once AuZex is implemented, this expression can be used for the numerical implementation of AuTra at moderate values of the real part of the argument, while its exponential still fits the range of values allowed for the variable used in the computation.
Asymptotic expansion
The asymptotic expansion for AuTra for large negative values of the argument can be obtained, inverting series for function SuTra. The inverse of $F$, id est, $G=F^{-1}$ has the following asymptotic:
$\displaystyle G(z)=\frac{z}{2}-\mathrm e^{-z}$ $\displaystyle -\frac{\mathrm e^z}{6}$ $\displaystyle +\frac{\mathrm e^{2 z}}{16}$ $\displaystyle -\frac{19 \mathrm e^{3 z}}{540}$ $\displaystyle +\frac{\mathrm e^{4 z}}{48}$ $\displaystyle -\frac{41 \mathrm e^{5 z}}{4200}$ $\displaystyle + \mathcal O( \mathrm e^{6 z}) $
The coefficients of the expansion above are calculated and evaluated with the Mathematica code below:
g0[z_] = z/2 - Exp[-z] + Sum[c[n] Exp[n z], {n, 1, 20}]
n = 1; s[n] = Series[g0[Log[t]] + 1 - g0[tra[Log[t]]], {t, 0, n + 1}]
u[n] = Extract[Solve[Coefficient[s[n], t^(n + 1)] == 0, c[n]], 1]
g[n, z_] = ReplaceAll[g0[z], t[n]]
For[n = 1, n < 20, n++;
s[n] = Series[ g[n - 1, Log[t]] + 1 - g[n - 1, tra[Log[t]]], {t, 0, n + 1}];
u[n] = Extract[Solve[Coefficient[s[n], t^(n + 1)] == 0, c[n]], 1];
g[n, z_] = ReplaceAll[g[n - 1, z], u[n]];
]
g[n, z]
Table[Coefficient[g[n, z], Exp[n z]], {n, 1, 20}]
N[Table[Coefficient[g[n, z], Exp[n z]], {n, 1, 20}], 18]
For some fixed integer $M$, define the primary approximation as truncation of the series above:
$\displaystyle G_M(z)=\frac{z}{2}-\mathrm e^{-z}$ $\displaystyle +\sum_{m=1}^{M} c_m \mathrm e^{mz} $
Function $G$ can be defined as limit
$\displaystyle G(z)=\lim_{n\rightarrow \infty} (G_M(\mathrm{ArcTra}^n(z))+n)$
AuTra can be expressed thirough $G$ with
$ \mathrm{AuTra}(z)=G(z)-G(0) \approx G(z)+1.1259817765745026$
The constant $G(0)$ can be interpreted also as coefficient $c_0$, id est, $c_0=G(0)$; then, finction $g$ can be defined with
$\displaystyle g_M(z)=\frac{z}{2}-\mathrm e^{-z}$ $\displaystyle +\sum_{m=0}^{M} c_m \mathrm e^{mz} $
and
$ \mathrm{AuTra}(z)=\lim_{n\rightarrow \infty} g_M(\mathrm{ArcTra}^n(z))$
This representation is used for the numericcal implementation of AuTra described below.
Numerical implementation of AuTra
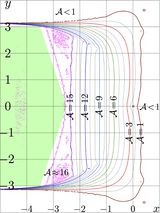
This section describe the complex double numerical implementation of AuTra. For $M=9$, the figure at right shows the agreement
$\displaystyle A_M(z)=-\lg\left( \frac{ |\mathrm{SuTra}(g_M(z))-z|}{ |\mathrm{SuTra}(g_M(z))|+|z|} \right)$
of the primary approximation $g_M$.
The thick outher loop indicates $\mathcal A=1$, function $g_M$ does not approximate AuTra. This cannot be improved increasing $M$. The inner loop corresponds to $\mathcal A=16$, and it looks a little bit irregular, that can be attributed to the rounding errors at the use of the complex double arithmetics. For the same reason, the level $\mathcal A=15$ also looks scratched.
The shaded region refers to $|y|<3$, $|y|<-2.5-1.5|y|$; in this region, the primary approximation provides of order of 16 decimal digits. This precision seems to be best that can be done for complex double implementation. Values of $g$ from the shaded region are qualified as "precise" and used for evaluation of AuTra also at other values of the argument, applying the transfer equation: Function ArcTra is applied to the argument so many times as necessary in order to bring it to the shaded region. Note that the shaded region happens to be almost twice wider, that the initial strip $|y|<\pi/2\approx 1.57$, where the asymptotic expansion is valid.
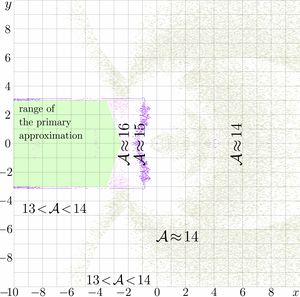
The agreement for the resulting secondary (and, perhaps, final) approximation is shown in figure at right. The figure indicates, that the implementation returns of order of 14 decimal digits. At least partially, the deviation can be attributed to the implementation of function SuTra, that is also implemented with 14 decimal digits. These 14 digits of precision are close to the maximum that can be realised with complex double arithmetics. This precision greatly exceeds the precision, required to plot the camera-ready pictures of the complex maps of the related functions.
References
Keywords
Abel function, AuZex Numeric implementation, Superfunction. SuZex Trappmann function,