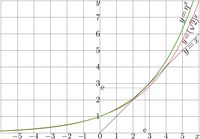
Base e1e
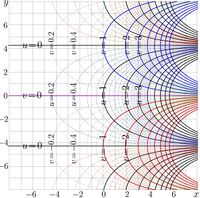
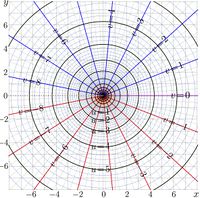
Base e1e refers to the value of base \(b= \eta =\exp(1/\mathrm e)\approx 1.4446678610\)
and corresponding exponential, SuperExponential (in particular, the tetration) and the inverse functions. In future, this may refer also to the highest Ackermann functions to this base.
The specific value of \(b\) corresponds to the single real fixed point of the exponential. For this case, the special formalism of exotic iteration had been developed. [1]
The special name, for example, Henryk constant, is required for the base \(~b=\exp(1/\mathrm e)\approx 1.4446678610~\) , and notation \(\eta\) is suggested for this value of \(b\).
Contents
Exponent and logarithm to base e1e
The complex maps of \(f=\exp_\eta\) and \(f=\log_\eta\) are shown in figures at right with lines \(u+\mathrm i v = f(x+\mathrm i y)\) in the \(x\),\(y\) plane. These pictures look similar to those for the case \(b=\sqrt{2}\approx 1.414\), see article Base sqrt2. and those for the case \(b=3/2=1.5\), see article Base 1.5.
Fixed points
Values of the fixed points and behaviour of the superfunctions and the Abel functions are pretty different for the similar values of base \(b\) mentioned above.
At base \(b=\sqrt{2}\approx 1.414\), there exist two real fixed points, \(L_1=2\) and \(L_2=4\).
At base \(b=\eta=\exp(1/\mathrm e)\approx 1.444\), there exist one real fixed point \(L=\mathrm e \approx 2.71\).
At base \(beta\), there exist no real fixed points, and the superexponential is supposed to approach the complex fixed points \(L\) and \(L^*\) at the infinity; correspondently, the AbelExponential, the ArcTetration \(\mathrm{ate}\) has branch points at these values.
The explicit plot of exponential to base \(\eta\)
Superexponentials to base \(\eta\)
For the base \(b=\eta=\exp(1/\mathrm e)\), the asymptotic expansion of the superexponential can be written in the following form:
\(\displaystyle \tilde F(z)=\mathrm e\cdot\left(1-\frac{2}{z}\left( 1+\sum_{m=1}^{M} \frac{P_{m}\big(-\ln(\pm z) \big)}{(3z)^m} +\mathcal{O}\!\left(\frac{|\ln(z)|^{m+1}}{z^{m+1}}\right) \right) \right) \)
where \(P\) are polynomials;
\( P_{1}(t)=t \)
\(P_{2}(t)=t^{2}+t+1/2 \)
\(P_{3}(t)=t^{3}+\frac{ 5}{ 2}t^{2}+\frac{ 5}{2}t +\frac{ 7}{10} \)
\(P_{4}(t)=t^{4}+\frac{13}{ 3}t^{3}+\frac{ 45}{6}t^{2}+\frac{53}{10}t +\frac{ 67}{60} \)
\(P_{5}(t)=t^{5}+\frac{77}{12}t^{4}+\frac{101}{6}t^{3}+\frac{83}{ 4}t^{2}+\frac{653}{60}t+\frac{2701}{1680}\)
...
More polynomials \(P\) can be calculated substituting representation \(\tilde F\) into the transfer equation
\( \tilde F(z\!+\!1)=\exp_\eta(\tilde F(z))\)
and performing the asymptotic analysis at large \(|z|\).
References
- ↑
http://www.ams.org/journals/mcom/0000-000-00/S0025-5718-2012-02590-7/S0025-5718-2012-02590-7.pdf
http://mizugadro.mydns.jp/PAPERS/2012e1eMcom2590.pdf H.Trappmann, D.Kouznetsov. Computation of the Two Regular Super-Exponentials to base exp(1/e). Mathematics of Computation. Math. Comp., v.81 (2012), p. 2207-2227. ISSN 1088-6842(e) ISSN 0025-5718(p)