BesselY0
BesselY0, called also Neumann function, and also \(\mathrm{BesselY}_0\) or simply \(Y_0\) is kind of Bessel function (or Cylindric function), solution \(f=f(z)\) of the Bessel equation
- \( \!\!\!\!\!\!\!\!\!\! (1) ~ ~ ~ \displaystyle f''+f'/z+f=0\)
with integral representation
- \(\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle Y_0(x)=\frac{-2}{\pi} \int_0^\infty \cos(x \cosh(t)) \mathrm d t\)
valid at least for \(x>0\).
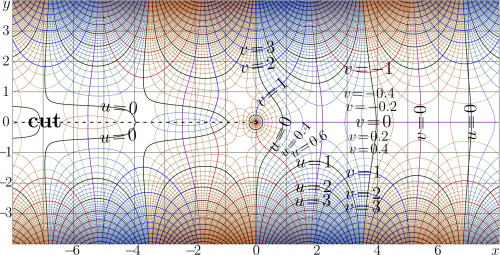
The explicit plot of \(Y_0\) of real argument is shown at the upper right corner, for comparison, \(J_0\) and \(J_1\) are also plotted; the complex map of \(Y_0\) is shown below.
Contents
Various notations
In the literture, and in particular, in the first editions of the tables by Granshtein,Ryzhik, BesselY0 is called Neumann function and denoted \(N_0\). In the latest editions and in the tables by Abramowits,Stegun, notation \(Y_0\) is used. In Mathematica, BesselY0(z) can be accessed with BesselY[0,z] and is interpreted as "Bessel function of Second kind" [1]
Relation to \(J_0\)
In the upper half–plane, id est, for \(\Re(z)>0\), the following relation with BesselJ0 takes place:
- \(Y_0(z)=Y_0(-z)+2~ \mathrm i~ J_0(-z)\)
At \(\Re(z)<0\), the similar relation is valid:
- \(Y_0(z)=Y_0(-z)- 2~ \mathrm i~ J_0(-z)\)
These formulas are used for evaluation of \(Y_0(z)\) at \(\Re(z)<0\) in the C++ complex(double) implementation Bessely0.cin .
Behavior at zero
- \( \!\!\!\!\!\!\!\!\!\! (2) ~ ~ ~ \displaystyle Y_0(z)=\frac{2 (\log (z)+\gamma -\log (2))}{\pi }+\frac{z^2 (-\log (z)-\gamma +1+\log (2))}{2 \pi }+\frac{z^4 (2 \log (z)+2 \gamma -3-2 \log (2))}{64 \pi }+O\left(z^6\right) \)
where \(~\gamma=\)EulerGamma\(~\approx 0.5772156649015329~\) is universal constant.
Expansion at large values of the argument
At large \(|z|\), the expansion of \(Y_0\) can be written in analogy with that for \(J_0\):
- \( \!\!\!\!\!\!\!\!\!\!\!\! (3) ~ ~ ~ \displaystyle J_0(z)=\sqrt{\frac{2}{\pi z}} \left( \left(\frac{1}{8 z} -\frac{75}{1024 z^3}+O\left(\frac{1}{z^5}\right)\right) \sin \left(z-\frac{\pi }{4}\right) +\left(1-\frac{9}{128 z^2}+\frac{3675}{32768 z^4}+O\left(\frac{1}{z^6}\right)\right) \cos \left(z-\frac{\pi }{4}\right) \right) \)
- \( \!\!\!\!\!\!\!\!\!\!\!\! (4) ~ ~ ~ \displaystyle Y_0(z)=\sqrt{\frac{2}{\pi z}} \left( \left(\frac{-1}{8 z}+\frac{75}{1024 z^3}+O\left(\frac{1}{z^5}\right)\right) \cos \left(z-\frac{\pi }{4}\right) +\left(1-\frac{9}{128 z^2}+\frac{3675}{32768 z^4}+O\left(\frac{1}{z^6}\right)\right) \sin \left(z-\frac{\pi }{4}\right) \right) \)
Keywords
Bessel function BesselJ0 BesselJ1 BesselH0
References
- ↑ http://mathworld.wolfram.com/BesselFunctionoftheSecondKind.html Bessel Function of the Second Kind
