Difference between revisions of "CosFT"

From TORI
Jump to: navigation, search
 
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)")
 
Line 1: Line 1:
−
[[CosFT]], or Cosinus Transform, refers to the integral transform with kernel $K(x,y)=\sqrt{\frac{2}{\pi}} \cos(xy)$;
 +
[[CosFT]], or Cosinus Transform, refers to the integral transform with kernel \(K(x,y)=\sqrt{\frac{2}{\pi}} \cos(xy)\);
   
−
for function $f$, the [[CosFT]]$f$ appears as $g$ defined with
 +
for function \(f\), the [[CosFT]]\(f\) appears as \(g\) defined with
   
−
$\displaystyle g(x)=\,$[[CosFT]]$f\,(x) \displaystyle =\sqrt{\frac{2}{\pi}} \int_0^\infty \cos(xy) \, f(y) \, \mathrm d y$
 +
\(\displaystyle g(x)=\,\)[[CosFT]]\(f\,(x) \displaystyle =\sqrt{\frac{2}{\pi}} \int_0^\infty \cos(xy) \, f(y) \, \mathrm d y\)
   
 
==[[SinFT]] and [[CosFT]]==
  
==[[SinFT]] and [[CosFT]]==
Line 9: Line 9:
 
[[CosFT]] often appears together with [[SinFT]];
  
[[CosFT]] often appears together with [[SinFT]];
   
−
the sine transform [[SinFT]] of function $f$ appears as $g=\,$[[SinFT]]$f$ with rofmula
 +
the sine transform [[SinFT]] of function \(f\) appears as \(g=\,\)[[SinFT]]\(f\) with rofmula
   
−
$\displaystyle g(x)=\sqrt{\frac{2}{\pi}} \int_0^\infty \sin(xy) \, f(y) \, \mathrm d y$
 +
\(\displaystyle g(x)=\sqrt{\frac{2}{\pi}} \int_0^\infty \sin(xy) \, f(y) \, \mathrm d y\)
   
−
It is assumed that function $f$ decays (or, at least, quickly oscillates) at infinity, in such a way that the integral converges.
 +
It is assumed that function \(f\) decays (or, at least, quickly oscillates) at infinity, in such a way that the integral converges.
   
−
Then, [[SinFT]]$^2=\,$[[CosFT]]$^2=\hat 1$, id est, the identity transform.
 +
Then, [[SinFT]]\(^2=\,\)[[CosFT]]\(^2=\hat 1\), id est, the identity transform.
   
 
==Numerical implementation==
  
==Numerical implementation==
   
−
[[CosFT]] can be implemented numerically through the [[CFT]] transform at the uniform grid at $N\!+\!1$ nodes; for array $f$, the SFT $g$ is defined with
 +
[[CosFT]] can be implemented numerically through the [[CFT]] transform at the uniform grid at \(N\!+\!1\) nodes; for array \(f\), the SFT \(g\) is defined with
   
−
$g_m=\,$[[CFT]]$\displaystyle f_m=$ $\displaystyle
 +
\(g_m=\,\)[[CFT]]\(\displaystyle f_m=\) \(\displaystyle
 
\frac{1}{2}\, f_0+\frac{(-1)^m}{2}\, f_{N} +
  
\frac{1}{2}\, f_0+\frac{(-1)^m}{2}\, f_{N} +
−
\sum_{n=1}^{N-1} \cos\left( \frac{\pi}{N} \,m\,n \right) \, f_n$
 +
\sum_{n=1}^{N-1} \cos\left( \frac{\pi}{N} \,m\,n \right) \, f_n\)
   
 
The [[Numerical recipes in C]] (http://numerical.recipes)
  
The [[Numerical recipes in C]] (http://numerical.recipes)
Line 36: Line 36:
 
ftp://ftp.cs.stanford.edu/cs/robotics/scohen/nr/cosft.c</ref>
  
ftp://ftp.cs.stanford.edu/cs/robotics/scohen/nr/cosft.c</ref>
   
−
At given number $N$ of nodes,
 +
At given number \(N\) of nodes,
−
the set of the nodes can be denoted with $x_n$ for $n=0 .. N$,
 +
the set of the nodes can be denoted with \(x_n\) for \(n=0 .. N\),
   
−
$\displaystyle
 +
\(\displaystyle
−
x_n=\sqrt{\frac{\pi}{N}}~ n$
 +
x_n=\sqrt{\frac{\pi}{N}}~ n\)
   
−
then, for $f_n=f(x_n)$, at large $N\gg 1$,
 +
then, for \(f_n=f(x_n)\), at large \(N\gg 1\),
−
the transform $~g(x)=\frac{2}{\pi}\int_0^\infty f(y)\,\cos(x\,y)\,\mathrm d y~$ is approximated with
 +
the transform \(~g(x)=\frac{2}{\pi}\int_0^\infty f(y)\,\cos(x\,y)\,\mathrm d y~\) is approximated with
   
−
$\displaystyle
 +
\(\displaystyle
−
g(x_m) \approx g_m = \sqrt{\frac{2}{N}}\, \left( \frac{f_0+(-1)^m f_N}{2} + \sum_{n=1}^{N-1} \, \cos\left( \frac{\pi}{N} \,m\,n \right) \, f_n\right)$
 +
g(x_m) \approx g_m = \sqrt{\frac{2}{N}}\, \left( \frac{f_0+(-1)^m f_N}{2} + \sum_{n=1}^{N-1} \, \cos\left( \frac{\pi}{N} \,m\,n \right) \, f_n\right)\)
   
 
==Eigenfunctions==
  
==Eigenfunctions==
Line 52: Line 52:
 
[[File:Cosftes16t300.jpg|360px|right]]
  
[[File:Cosftes16t300.jpg|360px|right]]
   
−
Eigenfunctions $F$ of the [[CosFT]] appear as even [[Oscillator function]]s.
+
Eigenfunctions \(F\) of the [[CosFT]] appear as even [[Oscillator function]]s.
   
 
The simplest of them is just Gaussian;
 
The simplest of them is just Gaussian;
   
−
$F(x)=\exp(-x^2/2)$
 +
\(F(x)=\exp(-x^2/2)\)
   
−
This property is used in the [[C++]] test. The thick segmented line in the explicit plots at right show the discrete representation of the Gaussian at the discrete grid with $N\!=\!4$ and $N\!=\!16$.
 +
This property is used in the [[C++]] test. The thick segmented line in the explicit plots at right show the discrete representation of the Gaussian at the discrete grid with \(N\!=\!4\) and \(N\!=\!16\).
   
 
The thin segmented line shows its [[SinFT]] transform, as it is approximated at this grid. The discrete representation and its CFT practically coincide; the deviation is smaller than the thicknesses of the lines.
  
The thin segmented line shows its [[SinFT]] transform, as it is approximated at this grid. The discrete representation and its CFT practically coincide; the deviation is smaller than the thicknesses of the lines.

Latest revision as of 18:47, 30 July 2019

CosFT, or Cosinus Transform, refers to the integral transform with kernel \(K(x,y)=\sqrt{\frac{2}{\pi}} \cos(xy)\);

for function \(f\), the CosFT\(f\) appears as \(g\) defined with

\(\displaystyle g(x)=\,\)CosFT\(f\,(x) \displaystyle =\sqrt{\frac{2}{\pi}} \int_0^\infty \cos(xy) \, f(y) \, \mathrm d y\)

SinFT and CosFT

CosFT often appears together with SinFT;

the sine transform SinFT of function \(f\) appears as \(g=\,\)SinFT\(f\) with rofmula

\(\displaystyle g(x)=\sqrt{\frac{2}{\pi}} \int_0^\infty \sin(xy) \, f(y) \, \mathrm d y\)

It is assumed that function \(f\) decays (or, at least, quickly oscillates) at infinity, in such a way that the integral converges.

Then, SinFT\(^2=\,\)CosFT\(^2=\hat 1\), id est, the identity transform.

Numerical implementation

CosFT can be implemented numerically through the CFT transform at the uniform grid at \(N\!+\!1\) nodes; for array \(f\), the SFT \(g\) is defined with

\(g_m=\,\)CFT\(\displaystyle f_m=\) \(\displaystyle \frac{1}{2}\, f_0+\frac{(-1)^m}{2}\, f_{N} + \sum_{n=1}^{N-1} \cos\left( \frac{\pi}{N} \,m\,n \right) \, f_n\)

The Numerical recipes in C (http://numerical.recipes) suggest the implementation through routines four1 and realft; however, for the serious applications, specification "float" should be replaced to something appropriate, for example, double, or complex double. [1][2][3][4]

At given number \(N\) of nodes, the set of the nodes can be denoted with \(x_n\) for \(n=0 .. N\),

\(\displaystyle x_n=\sqrt{\frac{\pi}{N}}~ n\)

then, for \(f_n=f(x_n)\), at large \(N\gg 1\), the transform \(~g(x)=\frac{2}{\pi}\int_0^\infty f(y)\,\cos(x\,y)\,\mathrm d y~\) is approximated with

\(\displaystyle g(x_m) \approx g_m = \sqrt{\frac{2}{N}}\, \left( \frac{f_0+(-1)^m f_N}{2} + \sum_{n=1}^{N-1} \, \cos\left( \frac{\pi}{N} \,m\,n \right) \, f_n\right)\)

Eigenfunctions

Cosftes04t300.jpg
Cosftes16t300.jpg

Eigenfunctions \(F\) of the CosFT appear as even Oscillator functions.

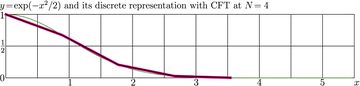
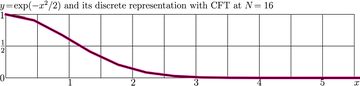
The simplest of them is just Gaussian;

\(F(x)=\exp(-x^2/2)\)

This property is used in the C++ test. The thick segmented line in the explicit plots at right show the discrete representation of the Gaussian at the discrete grid with \(N\!=\!4\) and \(N\!=\!16\).

The thin segmented line shows its SinFT transform, as it is approximated at this grid. The discrete representation and its CFT practically coincide; the deviation is smaller than the thicknesses of the lines.

References

  1. ↑ ftp://ftp.cpc.ncep.noaa.gov/wd51we/random_phase/four1.c
  2. ↑ ftp://ftp.cpc.ncep.noaa.gov/wd51we/random_phase/realft.c
  3. ↑ ftp://ftp.cs.stanford.edu/cs/robotics/scohen/nr/sinft.c
  4. ↑ ftp://ftp.cs.stanford.edu/cs/robotics/scohen/nr/cosft.c

Keywords

CosFT, FFT, Integral transform, SinFT,,,

Retrieved from "https://mizugadro.mydns.jp/t/index.php?title=CosFT&oldid=28406"