File:Ack4aFragment.jpg
Fragment of image http://mizugadro.mydns.jp/t/index.php/File:Ack4a600.jpg
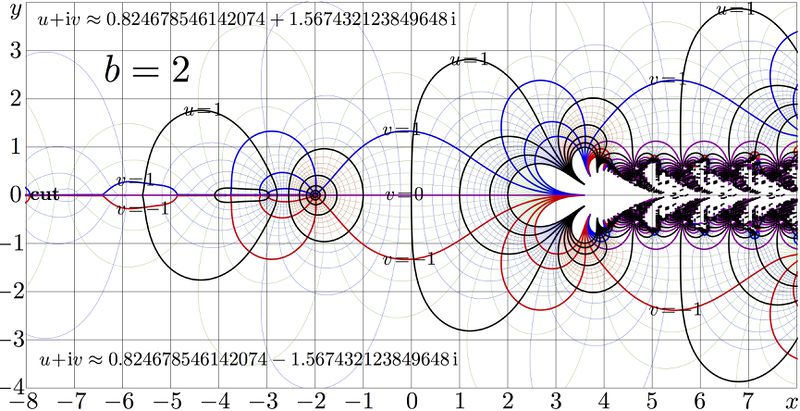
Complex map of tetration to base $b\!=\!2$
$u\!+\!\mathrm i v=\mathrm{tet}_b(x\!+\!\mathrm i y)$
Usage
This is fragment of image fig.3a (with improved resolution) of publication "Evaluation of holomorphic ackermanns", 2014. [1]
C++ Generator of map
Files ado.cin, conto.cin, tet2f4c.cin, Tet2f2048.inc, GLxw2048.inc should be loaded to the working directory in order to compile the code below.
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
#include <complex>
#define z_type std::complex<double>
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "conto.cin"
//#include "filog.cin"
z_type b=2.;
#include "tet2f4c.cin"
int main(){ int j,k,m,m1,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
//z_type Zo=z_type(.31813150520476413, 1.3372357014306895); // This is for b=e, not used here..
//z_type Zc=z_type(.31813150520476413,-1.3372357014306895);
int M=641,M1=M+1;
int N=402,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
// FILE *o;o=fopen("tet2m2.eps","w");ado(o,1604,804);
// FILE *o;o=fopen("tettenm2.eps","w");ado(o,1604,804);
// FILE *o;o=fopen("amsfig4dFragmen.eps","w");ado(o,1604,804);
FILE *o;o=fopen("amsfig4aFragmen.eps","w");ado(o,1604,804);
fprintf(o,"802 402 translate\n 100 100 scale 2 setlinecap 1 setlinejoin\n");
DO(m,M1)X[m]=-8.+.05*(m-.3);
DO(n,200)Y[n]=-4.+.02*n;
Y[200]=-.01;
Y[201]= .01;
for(n=202;n<N1;n++) Y[n]=-4.+.02*(n-1.);
for(m=-8;m<9;m++){M(m,-4)L(m,4)}
for(n=-4;n<5;n++){ M( -8,n)L(8,n)}
fprintf(o,".008 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){g[m*N1+n]=990999; f[m*N1+n]=909999;}
DO(n,N1){y=Y[n];
for(m=150;m<170;m++)
{x=X[m]; //printf("%5.2f\n",x);
z=z_type(x,y);
// c=tetb(z);
// c=F4TEN(z);
c=F4(z);
p=Re(c);q=Im(c);
if(p>-99999. && p<99999. && q>-99999. && q<99999. ){ g[m*N1+n]=p;f[m*N1+n]=q;}
d=c;
for(k=1;k<31;k++)
{ m1=m+k*20; if(m1>M) break;
// d=exp(a*d);
d=exp(d*log(2.));
p=Re(d);q=Im(d);
if(p>-99999. && p<99999. && q>-99999. && q<99999. ){ g[m1*N1+n]=p;f[m1*N1+n]=q;}
}
d=c;
for(k=1;k<31;k++)
{ m1=m-k*20; if(m1<0) break;
// d=log(d)/a;
d=log(d)/log(2.);
p=Re(d);q=Im(d);
if(p>-99999. && p<99999. && q>-99999. && q<99999. ){ g[m1*N1+n]=p;f[m1*N1+n]=q;}
}
}}
fprintf(o,"1 setlinejoin 2 setlinecap\n"); p=20;q=1;
for(m=-4;m<4;m++)for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N,(m+.1*n),-q, q); fprintf(o,".004 W 0 .6 0 RGB S\n");
for(m=0;m<4;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q, q); fprintf(o,".004 W .9 0 0 RGB S\n");
for(m=0;m<4;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q, q); fprintf(o,".004 W 0 0 .9 RGB S\n");
for(m=1;m<5;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p); fprintf(o,".03 W .9 0 0 RGB S\n");
for(m=1;m<5;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".03 W 0 0 .9 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (0. ),-p,p); fprintf(o,".03 W .6 0 .6 RGB S\n");
for(m=-4;m<5;m++) conto(o,g,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".03 W 0 0 0 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
//system( "ggv fig3.eps");
system("epstopdf amsfig4aFragmen.eps");
system( "open amsfig4aFragmen.pdf");
getchar(); system("killall Preview");
}
Latex Generator of labels
\documentclass{amsproc}
\usepackage{graphicx}
\usepackage{rotating}
\usepackage{hyperref}
\newcommand \sx {\scalebox}
\newcommand \rme {{\rm e}} %%
%\newcommand \rme {{e}} %%
\newcommand \rmi {{\rm i}} %%imaginary unity \newcommand \ds {\displaystyle}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\newcommand \ing \includegraphics
\usepackage{geometry}
\topmargin -94pt
\oddsidemargin -70pt
\paperwidth 1666pt
\paperheight 856pt
\textwidth 1900px
\textheight 900px
\begin{document}
\parindent 0pt
\newcommand \mapax {
\put(18,820){\sx{5}{$y$}}
\put(18,730){\sx{5}{$3$}}
\put(18,630){\sx{5}{$2$}}
\put(18,530){\sx{5}{$1$}}
\put(18,430){\sx{5}{$0$}}
\put(-14,329){\sx{5}{$-1$}}
\put(-14,229){\sx{5}{$-2$}}
\put(-14,129){\sx{5}{$-3$}}
\put(-14, 29){\sx{5}{$-4$}}
\put(14, 0){\sx{5}{$-8$}}
\put(114, 0){\sx{5}{$-7$}}
\put(214, 0){\sx{5}{$-6$}}
\put(314, 0){\sx{5}{$-5$}}
\put(414, 0){\sx{5}{$-4$}}
\put(514, 0){\sx{5}{$-3$}}
\put(614, 0){\sx{5}{$-2$}}
\put(714, 0){\sx{5}{$-1$}}
\put(844, 0){\sx{5}{$0$}}
\put(944, 0){\sx{5}{$1$}}
\put(1044, 0){\sx{5}{$2$}}
\put(1144, 0){\sx{5}{$3$}}
\put(1244, 0){\sx{5}{$4$}}
\put(1344, 0){\sx{5}{$5$}}
\put(1444, 0){\sx{5}{$6$}}
\put(1544, 0){\sx{5}{$7$}}
\put(1634, 0){\sx{5}{$x$}}
}
%\flushright{$b=\mathrm e \approx 2.71$}
{\begin{picture}(1620,850) %%%
\put(50,40){\ing{amsfig4aFragmen}} \mapax
\put(214,680){\sx{8}{$b=2$}}
\put(76,798){\sx{4}{$u\!+\!\mathrm i v \approx 0.824678546142074 + 1.567432123849648 \,\mathrm i$}}
\put(80,90){\sx{4}{$u\!+\!\mathrm i v \approx 0.824678546142074 - 1.567432123849648 \,\mathrm i$}}
\put(60,434){\sx{4}{\bf cut}}
\put(800,434){\sx{4}{$v\!=\!0$}}
\multiput(380,610)(555,105){3}{\sx{4}{$u\!=\!1$}}
\multiput(240,464)(555,105){4}{\sx{4}{$v\!=\!1$}}
\multiput(240,404)(555,-105){4}{\sx{4}{$v\!=\!-1$}}
\end{picture}}
\end{document}
Refrences
- ↑
http://article.sciencepublishinggroup.com/pdf/10.11648.j.acm.20140306.14.pdf
http://mizugadro.mydns.jp/PAPERS/2014acker.pdf D.Kouznetsov. Evaluation of holomorphic ackermanns. Applied and Computational Mathematics. Vol. 3, No. 6, 2014, pp. 307-314.
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html D.Kouznetsov. (2009). Solutions of F(z+1)=exp(F(z)) in the complex plane. Mathematics of Computation, 78: 1647-1670. DOI:10.1090/S0025-5718-09-02188-7.
https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
http://mizugadro.mydns.jp/BOOK/202.pdf
Д.Кузнецов. Суперфунцкии. Lambert Academic Publishing, 2014. (In Russian)
http://mizugadro.mydns.jp/BOOK/437.pdf D.Kouznetsov. Suparfunctions. Mizugadro, 2015. (In English)
http://myweb.astate.edu/wpaulsen/tetration.html William Paulsen. Tetration is repeated exponentiation. (2016). We can define $^0b = 1, ^1b = b, ^2b = b^b$, &3b = b^{b^b}$, etc. ..
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 06:10, 1 December 2018 |  | 3,457 × 1,776 (1.63 MB) | Maintenance script (talk | contribs) | Importing image file |
- You cannot overwrite this file.
File usage
The following 2 pages link to this file:
- File:Amsfig4aFragment.jpg (file redirect)
- File:Amsfig4aFragment.jpg (file redirect)