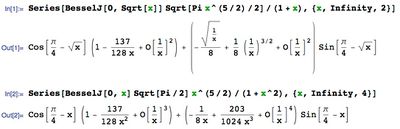Difference between revisions of "Mathematica"
| Line 60: | Line 60: | ||
==Bugs== |
==Bugs== |
||
As any other software, Mathematica has bugs. One of them is related to the asymptotic expansion of the [[Bessel function]] of non-trivial argument. |
As any other software, Mathematica has bugs. One of them is related to the asymptotic expansion of the [[Bessel function]] of non-trivial argument. |
||
| + | |||
| + | ===[[FullSimplify]]=== |
||
| + | |||
| + | Routine [[FullSimplify]] does not seem to handle well expressions with imaginary unity , I=\Sqrt[-1] . |
||
| + | |||
| + | Here is he example Let |
||
| + | <poem><nomathjax><nowiki> |
||
| + | b = (-1 + Exp[(-2*I)*q - 2*s])*(-1 + Exp[(2*I)*q - 2*s]) |
||
| + | |||
| + | c = (-1 + (q - I*s)^2)*(-1 + (q + I*s)^2) |
||
| + | |||
| + | a = b*c |
||
| + | |||
| + | U = FullSimplify[a] |
||
| + | </nowiki></nomathjax></poem> |
||
| + | |||
| + | The last evaluation does |
||
| + | $ |
||
| + | \left(-1+\mathrm{e}^{-2 s-2 i q}\right) |
||
| + | \left(-1+\mathrm{e}^{-2 s+2 i q}\right) |
||
| + | \left(-1+(q-i s)^2\right) |
||
| + | \left(-1+(q+i s)^2\right) |
||
| + | $ |
||
| + | |||
| + | instead of expected |
||
| + | $2 \mathrm{e}^{-2 s} \left(q^4+2 q^2 |
||
| + | \left(s^2-1\right)+\left(s^2+1\right)^2\right) (\cosh (2 s)-\cos (2 q)) |
||
| + | $ |
||
| + | |||
| + | Then, expression |
||
| + | <poem><nomathjax><nowiki> |
||
| + | FullSimplify[Im[U], {q>0, s>0}] |
||
| + | </nowiki></nomathjax></poem> |
||
| + | |||
| + | does |
||
| + | $\Im\left(\left(-1+e^{-2 s-2 i q}\right) |
||
| + | \left(-1+e^{-2 s+2 i q}\right) |
||
| + | \left(-1+(q-i s)^2\right) \left(-1+(q+i |
||
| + | s)^2\right)\right) |
||
| + | $ |
||
| + | |||
| + | instead of expected 0. |
||
| + | |||
| + | This can be verified with code |
||
| + | <poem><nomathjax><nowiki> |
||
| + | FullSimplify[b] FullSimplify[c] |
||
| + | </nowiki></nomathjax></poem> |
||
===Asymptotic expansion of the Bessel function=== |
===Asymptotic expansion of the Bessel function=== |
||
Revision as of 16:05, 1 December 2018
Mathematica is name of the programming language and software that supports this language, developed by the Wolfram corporation in the end of century 20 for simplification of mathematical expressions, solving equations, evaluation of functions, plotting graphics and other things that require some mathematics. For the beginning of century 21, Mathematica seems to be the strongest tool for the computation of analytical expressions and asymptotical analysis. The homepage of Wolfram [1] provides the indexed description.
The "official name" of the language used to program for this software is Wolfram language [2].
Up to 2016, there is no other software known to use the same language, nor other language to handle Mathematica. For this reason, for users, (who use only mathematica language dealing with this software), there is no reason to make strong difference between the software and its language.
In addition, term Mathematica may refer to Mathematics, the special kind of science, that deal with abuse of terms, invented namely for this. Mathematics is important for all other sciences, excluding, perhaps, the so-called Female logics.
Both software and language of Mathematica is important tool for mathematics. The mathematica software has relatively few bugs. One exampe when Mathematica gives non-expected output is shown in figure at right.
Contents
Usable by beginners
Mathematica language is close to the conventional way of writing of formulas. This allows the beginners to work with meaningful and non-trivial expressions knowing close to nothing about the structure of the language.
Support of Mathematica
Mathematica has strong service of support of users. In many cases, the problem with software can be quickly assisted and solved. Often, if a bug is reported to the Wolfram, then this bug does not appear in the later versions.
Use of Mathematica in TORI
Mathematica is advanced tool very useful for any non–trivial research. In particular, the asymptotical analysis with function Series happened to be very efficient in calculation the coefficients for the approximation for the superfunctions and Abel functions using the expansions in vicinity of the Fixed points; in particular, the numerical implementations for tetration, ArcTetration, SuperFactorial, Abel Factorial, etc.; of order of a dozen coefficients of the asymptotic expansion can be calculated analytically in the real time. (If manually, each such a calculus could take years, if at al.)
Mathematica has incorporated function Nest, that means iteration of function. The superfunctions mentioned above can be easy expressed through the Nest. However, in the current version (at least up to year 2011), the only natural constants are allowed as values of the number of iterations. Fore some function $f$, the $f^c$ is allowed only for an integer values of $c$ (reducible to an integer constant); any other value causes the error messages. Hope, in future versions, this problem will be fixed.
Competitors
The main competitor of Mathematica seems to be Maple (software). In year 2007, the release of Maple 10 happened to be buggy, and especially poor and slow was the graphical support. Two examples of this are presented in the poem Maple and tea[3].
Hope, the future versions become better.
Some functions of Mathematica can be performed also with Matlab and Labview.
Development
The development of Mathematica seems to be rather extensive than intensive: instead of to force to work better the existing functions, the new options are added. The Nest function is only one or examples.
The internationalization of Mathematica happened to be very dangerous. Many languages supported by Mathematica, are not installed in the most of computers. This means, that the occasional switch to some non–trivial language makes the Mathematica unusable: the marks of buttons in the menu disappear, and it is almost impossible to find the correct combination of arrows to return the English. If such a case is identified, then another computer with non–broken Mathematica can be used for counting of buttons, bringing the problematic Mathematica installation to the menu of languages (and allows to recover English, then system of menu and the correct response to the functional keys also recover).
Images
Some images used in TORI are generated with Mathematica. Often, such the generators of images in Mathematica allow very quick programming. However, the quality of these images is poor compared to that achievable with the specialized C++ programs; files are huge but the resolution is low. Especially poor are the contour plots of singular functions. The standard mathematica routine does not handle the singularities and draws the isolines even in the regions where the correct drawing is not possible.
Perhaps, the quality of the Mathematica graphics could be significantly improved at the implementation of some analogy of the algorithm conto.cin for the implicit plots.
The good quality of the PNG and [[J{G]] pictures can be achieved if the initial graphic is plotted with huge reserve of resolution, and then compressed with loss of resolution. However, for non–trivial functions, the plotting of such graphicstakes a lot of CPU time and requires strong nerves and patience of the user. For this reason, for TORI, the most of graphics are generated by the C++ codes with the EPS output.
Bugs
As any other software, Mathematica has bugs. One of them is related to the asymptotic expansion of the Bessel function of non-trivial argument.
FullSimplify
Routine FullSimplify does not seem to handle well expressions with imaginary unity , I=\Sqrt[-1] .
Here is he example Let
b = (-1 + Exp[(-2*I)*q - 2*s])*(-1 + Exp[(2*I)*q - 2*s])
c = (-1 + (q - I*s)^2)*(-1 + (q + I*s)^2)
a = b*c
U = FullSimplify[a]
The last evaluation does $ \left(-1+\mathrm{e}^{-2 s-2 i q}\right) \left(-1+\mathrm{e}^{-2 s+2 i q}\right) \left(-1+(q-i s)^2\right) \left(-1+(q+i s)^2\right) $
instead of expected $2 \mathrm{e}^{-2 s} \left(q^4+2 q^2 \left(s^2-1\right)+\left(s^2+1\right)^2\right) (\cosh (2 s)-\cos (2 q)) $
Then, expression
FullSimplify[Im[U], {q>0, s>0}]
does $\Im\left(\left(-1+e^{-2 s-2 i q}\right)
\left(-1+e^{-2 s+2 i q}\right)
\left(-1+(q-i s)^2\right) \left(-1+(q+i
s)^2\right)\right)
$
instead of expected 0.
This can be verified with code
FullSimplify[b] FullSimplify[c]
Asymptotic expansion of the Bessel function
The bug with Bessel function appeares in the calculus of the pinhole waveguide [4] in the paraxial approximation. Fortunately, one of tests of the self–consistency of the result (See TORI axioms) had revealed the bug, and the wrong calculus had not been published. In the simplified form (parameters are set to unity), the code, that shows this bug, is copy pasted below.
The example refers to the asymptotic expansion of function
$\sqrt{\frac{\pi x^{5/2}}{2}}$ $\displaystyle \frac{J_0\big(\sqrt{x}\,\big)}{1+x} $
at large $x\gg 1$. The leading $\sqrt{\frac{\pi x^{5/2}}{2}}$ does no matter for the bug, but this factor simplifies a bit the output (to fit one line at the screen). The simple form of the example is shown in the figure at the top.
The corresponding code is
Series[BesselJ[0, Sqrt[x]] Sqrt[Pi x^(5/2)/2]/(1 + x), {x, Infinity, 2}]
It produces output
$\displaystyle \left(-\frac{\sqrt{\frac{1}{x}}}{8}+\frac{1}{8}
\left(\frac{1}{x}\right)^{3/2}+O\left(\left(\frac{1}{x}
\right)^2\right)\right) \sin \left(\frac{\pi
}{4}-\sqrt{x}\right)+\left(1-\frac{137}{128
x}+O\left(\left(\frac{1}{x}\right)^2\right)\right) \cos
\left(\frac{\pi }{4}-\sqrt{x}\right)$
instead of expected
$\displaystyle \left(-\frac{\sqrt{\frac{1}{x}}}{8}+\frac{203}{1024}
\left(\frac{1}{x}\right)^{3/2}+O\left(\left(\frac{1}{x}
\right)^{5/2}\right)\right) \sin \left(\frac{\pi
}{4}-\sqrt{x}\right)+\left(1-\frac{137}{128
x}+O\left(\left(\frac{1}{x}\right)^2\right)\right) \cos
\left(\frac{\pi }{4}-\sqrt{x}\right)$
At the same time, code
Series[BesselJ[0, x] Sqrt[Pi/2] x^(5/2)/(1 + x^2), {x, Infinity, 4}]
produces the output
$\displaystyle \left(-\frac{1}{8 x}+\frac{203}{1024
x^3}+O\left(\left(\frac{1}{x}\right)^4\right)\right)
\sin \left(\frac{\pi
}{4}-x\right)+\left(1-\frac{137}{128
x^2}+O\left(\left(\frac{1}{x}\right)^3\right)\right)
\cos \left(\frac{\pi }{4}-x\right)
$
That seems to be correct.
The same or similar bug appears at some of Series with the Hankel function HankelH1, if the square root of parameter of expansion appears in the argument.
It seems, the routine Series still can be used for the asymptotic expansion of the cylindric functions, but the argument of the Cylindric function should be parameter of expansion; over-vice, the coefficients of the resulting expansion may be wrong.
TeXForm conversion
Generator of the Latex code that can be used to include the formula into the manuscript (for submission into some scientific journal) or into some wiki, does not generate code with image identical to that Mathematica shows. Formulas in the example above are generated with the following code:
The [[Latex[[ scripts it generates, are
\left(-\frac{\sqrt{\frac{1}{x}}}{8}+\frac{1}{8}
\left(\frac{1}{x}\right)^{3/2}+O\left(\left(\frac{1}{x
}\right)^2\right)\right) \sin \left(\frac{\pi
}{4}-\sqrt{x}\right)+\left(1-\frac{137}{128
x}+O\left(\left(\frac{1}{x}\right)^2\right)\right)
\cos \left(\frac{\pi }{4}-\sqrt{x}\right)
and
\left(-\frac{1}{8 x}+\frac{203}{1024
x^3}+O\left(\left(\frac{1}{x}\right)^4\right)\right)
\sin \left(\frac{\pi
}{4}-x\right)+\left(1-\frac{137}{128
x^2}+O\left(\left(\frac{1}{x}\right)^3\right)\right)
\cos \left(\frac{\pi }{4}-x\right)
The result (even if it is correct) appears in the form, different from that the formula appears in the Mathematica frame. For example, this bug requires some efforts in order to trace the bug with asymptotic expansion, mentioned in the previous subsection.
Simplification failure
FullSimplify[c^(1-p)^(-1) - c*(c^(1-p)^(-1))^p,{c>1,p>1}]
does
$\rm c^{\frac{1}{1-p}}-c
\left(c^{\frac{1}{1-p}}\right)^p$
instead of expected 0
The change of variable, replacement of $p$ to $1+r$ leads to the expected result:
FullSimplify[ ReplaceAll[c^(1-p)^(-1) - c*(c^(1-p)^(-1))^p, p -> 1+r], {c>1,r>0}]
confirms, that the result should be 0 .
Warning
Practically every software has bugs. The bugs mentioned above should not be considered as serious objection against use of the Mathematica software.
The same refers also to TORI. TORI is initially planned to present namely outstanding concepts, concepts that stay out of the main stream of development of science and business. Every serious deviation from the main stream requires justification. This justification looks as critics, but it should not be interpreted as individual targeting of any person nor any company. This critics also may contain bugs, errors. Please, let the Editor know about them, and the errors will be corrected as soon as possible.
References
- ↑ http://www.wolfram.com/mathematica/
- ↑ http://www.wolfram.com/language/ Wolfram Language.
- ↑ http://budclub.ru/k/kuznecow_d_j/maple.shtml D.Kouznetsov. Maple and Tea (2007)
- ↑ http://www.academicjournals.org/app/webroot/ebook/journal1414510635_IJPS%20-%2030th%20Oct,%202014%20Issue.pdf#page=12 Makoto Morinaga. Guiding of light with pinholes. hysical Sciences Volume 9 Number 20 30 October, 2014 ISSN 1992-1950, pages 444-453