Difference between revisions of "Natural tetration"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| Line 1: | Line 1: | ||
| − | [[File:TetPlotU.png|224px|left|thumb| |
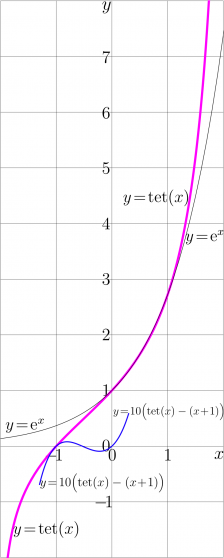
+ | [[File:TetPlotU.png|224px|left|thumb|\(y\!=\!\mathrm{tet}(x)~\), \(~y\!=\!e^x~\) and \(~y\!=\! 10\big(\mathrm{tet}(x)-(x\!+\!1)\big)\)]] |
| − | '''Natural tetration''' is [[tetration]] to the base |
+ | '''Natural tetration''' is [[tetration]] to the base \(\mathrm e=\exp(1)\approx 1.71~\). |
| − | Natural tetration is denoted as |
+ | Natural tetration is denoted as \(\mathrm {tet}\) or \(\mathrm {tet}_{\mathrm e}\); it satisfies the [[transfer equation]] |
| − | : |
+ | : \(\exp(\mathrm{tet}(z))= \mathrm{tet}(z\!+\!1)\) |
Also the initial condition |
Also the initial condition |
||
| − | : |
+ | : \(\mathrm{tet}(0)=1\) |
is assumed. |
is assumed. |
||
The asymptotic behavior at large values of the imaginary part of the argument is exponential approach the [[fixed point]] of [[logarithm]] through function [[Filog]] |
The asymptotic behavior at large values of the imaginary part of the argument is exponential approach the [[fixed point]] of [[logarithm]] through function [[Filog]] |
||
| − | : |
+ | : \(\!\!\!\! |
| − | L=\mathrm{Filog}(1)\approx 0.31813150520476413531+1.3372357014306894089\, i |
+ | L=\mathrm{Filog}(1)\approx 0.31813150520476413531+1.3372357014306894089\, i \) |
| − | in the upper half-plane and |
+ | in the upper half-plane and \(L^*\) |
in the lower half-plane. See the spacial article [[Filog]]. |
in the lower half-plane. See the spacial article [[Filog]]. |
||
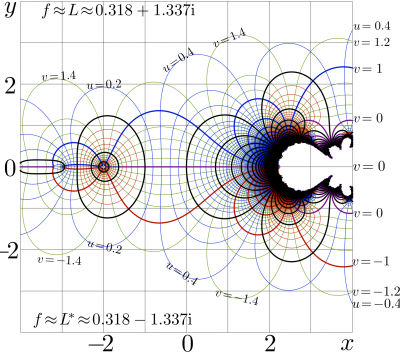
| − | [[File:B271t.png|400px|thumb|[[Complex map]] of |
+ | [[File:B271t.png|400px|thumb|[[Complex map]] of \(f=u\!+\!\mathrm i v=\mathrm{tet}(x\!+\!\mathrm i y)~\) in the \(x,y\) plane]] |
Natural tetration can be evaluated with the [[Iterated Cauchi]] algorithm |
Natural tetration can be evaluated with the [[Iterated Cauchi]] algorithm |
||
<ref name="analuxp"> |
<ref name="analuxp"> |
||
| Line 24: | Line 24: | ||
Along the real axis, the natural tetration shows fast growth, faster than any exponential and faster than any finite combinaiton of exponentials. |
Along the real axis, the natural tetration shows fast growth, faster than any exponential and faster than any finite combinaiton of exponentials. |
||
| − | Function |
+ | Function \(\mathrm {tet}(z)\) is holomorphic in the whole complex plane except the line \(\Re(z)\le -2\). |
Due to the wide range of holomorphism, and the simple properties, tetration is most important among various [[superfunction]]s of the exponential; |
Due to the wide range of holomorphism, and the simple properties, tetration is most important among various [[superfunction]]s of the exponential; |
||
an other supedfunciotn can be expressed with |
an other supedfunciotn can be expressed with |
||
| − | : |
+ | : \(\mathrm{sexp}(z)=\mathrm{tet}(z+\eta(z))\) |
| − | where |
+ | where \(\eta\) is holomorphic periodic function with period unity, |
| − | The exponential growth of |
+ | The exponential growth of \(\eta(z)\) in the direction of the imaginary axis reduces the range of holomorphism of such a superexponential, destroying its apymptotic approach to \(L\) and \(L^*\). |
| − | Inverse of the natiral tetration is denoted with symbol |
+ | Inverse of the natiral tetration is denoted with symbol \(\mathrm {ate}=\mathrm {tet}^{-1}\). |
| − | The pair of functions |
+ | The pair of functions \(\mathrm {tet}\) and \(\mathrm{ate}\) |
allows the efficient evaluation of the iteration of exponential, |
allows the efficient evaluation of the iteration of exponential, |
||
| − | : |
+ | : \(\exp^c(z)=\mathrm{tet}(c+\mathrm{ate}(z))\) |
| − | The number |
+ | The number \(c\) of iterations has no need to be integer; in particular, it can be a fration, an irrational number of even a complex number. |
The non–integer iterations of exponential give the class of functions that grow faster than any polynomial but slower than any exponential. |
The non–integer iterations of exponential give the class of functions that grow faster than any polynomial but slower than any exponential. |
||
==Approximations with elementary functions== |
==Approximations with elementary functions== |
||
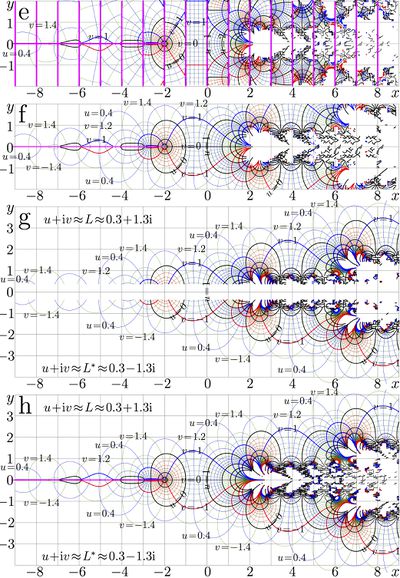
| − | [[File:Analuxp01u400.jpg|400px|thumb| Maps of various approximations |
+ | [[File:Analuxp01u400.jpg|400px|thumb| Maps of various approximations \(f\) of tetration; \(u+\mathrm i v= f(x+\mathrm i y)\)]] |
Several approximations of tetration and arctetration are described |
Several approximations of tetration and arctetration are described |
||
| Line 56: | Line 56: | ||
Natural tetration seems to be the only function with this property. |
Natural tetration seems to be the only function with this property. |
||
| − | Map e corresponds to the "linear" approximation |
+ | Map e corresponds to the "linear" approximation \(f=\mathrm{uxp}\) by M.H.Hooshmand |
<ref name="hooshmand"> |
<ref name="hooshmand"> |
||
http://www.tandfonline.com/doi/full/10.1080/10652460500422247 |
http://www.tandfonline.com/doi/full/10.1080/10652460500422247 |
||
| Line 62: | Line 62: | ||
</ref> |
</ref> |
||
| − | + | \( \displaystyle |
|
f(z)=\mathrm{uxp}(z)=\!\left\{ |
f(z)=\mathrm{uxp}(z)=\!\left\{ |
||
\begin{array}{ccccccc} |
\begin{array}{ccccccc} |
||
| Line 70: | Line 70: | ||
\end{array} |
\end{array} |
||
\right. |
\right. |
||
| + | \) |
||
| − | $ |
||
The sequence of vertical cutlines separate the complex plane to the set of almost iindependent strips, where the approximation is holomorphic. |
The sequence of vertical cutlines separate the complex plane to the set of almost iindependent strips, where the approximation is holomorphic. |
||
| Line 76: | Line 76: | ||
| − | Map f corresponds to the approximation |
+ | Map f corresponds to the approximation \(\mathrm{Fit}_3\) constructed in the following way: |
| − | + | \(s_2(z)= \exp\!\Big(\exp(z-2.51)\Big)-0.6+0.08(z\!+\!1)\) |
|
| − | + | \(\mathrm{fit}_2(z) \!=\!\) \( |
|
\ln(2\!+\!z) |
\ln(2\!+\!z) |
||
+ (1\!+\!z)\left( |
+ (1\!+\!z)\left( |
||
| Line 87: | Line 87: | ||
\Big(\!\mathrm e\! -2\! +\! \ln\frac{4}{3} \Big) |
\Big(\!\mathrm e\! -2\! +\! \ln\frac{4}{3} \Big) |
||
- \ln 2 |
- \ln 2 |
||
| − | \right) |
+ | \right)\) |
| − | + | \(\mathrm{fit}_3(z)=0.6\!~\mathrm{fit}_{2}(z)+0.4\!~\ln\big( \mathrm{fit}_{2}(z+1)\big)\) |
|
| − | + | \(\mathrm{Fit}_3(z)= \left\{\!\! |
|
\begin{array}{ccccc cc} |
\begin{array}{ccccc cc} |
||
\ln\!\big({\rm Fit}_{3}(z\!+\!1)\big) &{~\rm at}&~ \!&\! \!&\! \Re(z) \!&\! \le \!&\! -1 \!\\ |
\ln\!\big({\rm Fit}_{3}(z\!+\!1)\big) &{~\rm at}&~ \!&\! \!&\! \Re(z) \!&\! \le \!&\! -1 \!\\ |
||
| Line 97: | Line 97: | ||
\exp\!\big({\rm Fit}_{3}(z\!-\!1)\big) &{~\rm at}&~ 0 \!&\! < \!&\! \Re(z) \!& |
\exp\!\big({\rm Fit}_{3}(z\!-\!1)\big) &{~\rm at}&~ 0 \!&\! < \!&\! \Re(z) \!& |
||
\end{array} |
\end{array} |
||
| − | \right. |
+ | \right.\) |
| − | Constants in definition of function |
+ | Constants in definition of function \(s\) have rather historical than mathematical meaning, because they were used to guess the asymptotic behavior of tetration, while the precise algorithm for the evaluation had not yet been discovered. Using the precise implementation, the approxximation can be improved. |
Map g corresponds to the asymptotic representation |
Map g corresponds to the asymptotic representation |
||
| − | + | \(f(z)=\mathrm{fit}_6(z) =\) \( |
|
\left\{ |
\left\{ |
||
\begin{array} |
\begin{array} |
||
| Line 111: | Line 111: | ||
\exp\Big(\mathrm{fit}_6(z\!-\!1)\Big)~,~ \Re(z)\ge -8 |
\exp\Big(\mathrm{fit}_6(z\!-\!1)\Big)~,~ \Re(z)\ge -8 |
||
\end{array} |
\end{array} |
||
| − | \right. |
+ | \right.\) |
| − | for |
+ | for \(\Im(z)>0.5\) and \(f(z)=\mathrm{fit}_6(z^*)^*\) for \(\Im(z)<0.5\) ; In the map, the strip of intermediate values \(|y|<1/2\) is left empty. |
| − | In formula above, |
+ | In formula above, \(L\approx 0.31813150520476413 + 1.3372357014306895 \,\mathrm i\) is [[fixed point]] of logarithm, \(L=\ln(L)\). |
| − | For [[Natural tetration]], the increment |
+ | For [[Natural tetration]], the increment \(k=L\). |
| − | Parameter |
+ | Parameter \(r\) provides the match of the two asymptotics. It is fundamental mathematical constant; |
| − | + | \(r \approx 1.075820830781 - 0.9466419207254 \, \mathrm i\) . |
|
This precision seems to be sufficient for the applications; however, the improvement of the precision may be subject of the additional research. |
This precision seems to be sufficient for the applications; however, the improvement of the precision may be subject of the additional research. |
||
| Line 127: | Line 127: | ||
</ref>. |
</ref>. |
||
| − | In principle, the approximations |
+ | In principle, the approximations \(\mathrm{Fit}_3\), shown in map e, and \(\mathrm{Fit}_6\), shown in map f, allow to implement tetration in the whole complex plane with at least 3 defimal figures; this precision is sufficient to make camera–ready illustrations of properties of tetration. Historically, approximations \(\mathrm{fit}_6\) and \(\mathrm{Fit}_6\) were obtained after to implement the tetration through the Cauchi integral, when not only the limiting value \(L\) of tetration had been revealed, but also the exponential approaching of tetration to this value. |
==Numerical implementation== |
==Numerical implementation== |
||
| Line 136: | Line 136: | ||
Implementation of the corresponding [[arctetration]] is loaded as [[fslog.cin]]. |
Implementation of the corresponding [[arctetration]] is loaded as [[fslog.cin]]. |
||
The name of the routine, FSLOG, corresponds the the idea to name arctetration with identifier "super logarithm". The name [[Superlogarithm]] causes confusions, it makes an impression that it is [[superfunction]] of logarithm. |
The name of the routine, FSLOG, corresponds the the idea to name arctetration with identifier "super logarithm". The name [[Superlogarithm]] causes confusions, it makes an impression that it is [[superfunction]] of logarithm. |
||
| − | One superfunction |
+ | One superfunction \(G\) of logarithm can be expressed through the tetration, namely, \(G(z)=\mathrm{tet}(-z)\), which is not arctetration. For this reason, the name "fslog" is not good. However, for the historic reason, the name of the routine remains. As soon as the most efficient algorithms for evaluation of tetration and arctetration will be implemented, the implementations may have more understandable names TET and ATE. |
==Fixed points and Superfunction== |
==Fixed points and Superfunction== |
||
| − | For [[natural tetration]], the real [[fixed point]] |
+ | For [[natural tetration]], the real [[fixed point]] \(L_{\mathrm e,4,0} \!=\! L_{\mathrm e, 4,0} \!\approx\! -1.8503545290271812\) |
is used to construct the superfunction of tetration, the fifth [[Ackermann function]], called [[natural pentation]]; |
is used to construct the superfunction of tetration, the fifth [[Ackermann function]], called [[natural pentation]]; |
||
| − | + | \(\mathrm{pen}=A_{\mathrm e,5}\) |
|
For [[pentation]], the [[tetration]] tet is interpreted as the [[transfer function]]. Pentation satisfies the [[transfer equation]] |
For [[pentation]], the [[tetration]] tet is interpreted as the [[transfer function]]. Pentation satisfies the [[transfer equation]] |
||
| − | + | \(\mathrm{pen}(z\!+\!1)=\mathrm{tet}\Big(\mathrm{pen}(z)\Big)\) |
|
==Keywords== |
==Keywords== |
||
| Line 165: | Line 165: | ||
http://link.springer.com/article/10.1007/s10444-017-9524-1 |
http://link.springer.com/article/10.1007/s10444-017-9524-1 |
||
| − | William Paulsen and Samuel Cowgill. Solving |
+ | William Paulsen and Samuel Cowgill. Solving \(F(z+1)=b^{F(z)}\) in the complex plane. Advances in Computational Mathematics, 2017 March 7, p. 1–22 |
http://en.citizendium.org/wiki/Tetration |
http://en.citizendium.org/wiki/Tetration |
||
Revision as of 18:26, 30 July 2019
Natural tetration is tetration to the base \(\mathrm e=\exp(1)\approx 1.71~\).
Natural tetration is denoted as \(\mathrm {tet}\) or \(\mathrm {tet}_{\mathrm e}\); it satisfies the transfer equation
- \(\exp(\mathrm{tet}(z))= \mathrm{tet}(z\!+\!1)\)
Also the initial condition
- \(\mathrm{tet}(0)=1\)
is assumed.
The asymptotic behavior at large values of the imaginary part of the argument is exponential approach the fixed point of logarithm through function Filog
- \(\!\!\!\! L=\mathrm{Filog}(1)\approx 0.31813150520476413531+1.3372357014306894089\, i \)
in the upper half-plane and \(L^*\) in the lower half-plane. See the spacial article Filog.
Natural tetration can be evaluated with the Iterated Cauchi algorithm [1].
Along the real axis, the natural tetration shows fast growth, faster than any exponential and faster than any finite combinaiton of exponentials.
Function \(\mathrm {tet}(z)\) is holomorphic in the whole complex plane except the line \(\Re(z)\le -2\). Due to the wide range of holomorphism, and the simple properties, tetration is most important among various superfunctions of the exponential; an other supedfunciotn can be expressed with
- \(\mathrm{sexp}(z)=\mathrm{tet}(z+\eta(z))\)
where \(\eta\) is holomorphic periodic function with period unity, The exponential growth of \(\eta(z)\) in the direction of the imaginary axis reduces the range of holomorphism of such a superexponential, destroying its apymptotic approach to \(L\) and \(L^*\).
Inverse of the natiral tetration is denoted with symbol \(\mathrm {ate}=\mathrm {tet}^{-1}\).
The pair of functions \(\mathrm {tet}\) and \(\mathrm{ate}\) allows the efficient evaluation of the iteration of exponential,
- \(\exp^c(z)=\mathrm{tet}(c+\mathrm{ate}(z))\)
The number \(c\) of iterations has no need to be integer; in particular, it can be a fration, an irrational number of even a complex number.
The non–integer iterations of exponential give the class of functions that grow faster than any polynomial but slower than any exponential.
Contents
Approximations with elementary functions
Several approximations of tetration and arctetration are described [1][2].
Complex maps for several approximations of tetration are shown in figure at right. Numeration of maps begins with letter e, in order to avoid confusion with similar figure 1 from [1], where equilimes of logamplitude and phase are drown, instead of real and imaginary parts in figure at right. Due to the transfer equation, the change from logamplitude and phase to real and imaginary part are almost equivalent to the translation of all the map for unity along the real axis. Natural tetration seems to be the only function with this property.
Map e corresponds to the "linear" approximation \(f=\mathrm{uxp}\) by M.H.Hooshmand [3]
\( \displaystyle f(z)=\mathrm{uxp}(z)=\!\left\{ \begin{array}{ccccccc} \ln\!\big({\rm uxp}(z\!+\!1)\big) &{\rm at} &~ \!&\! \!&\! \Re(z) \!&\! \le \!&\!\! -1\! \\ z + 1 &{\rm at} & -1 \!&\! < \!&\! \Re(z) \!&\! \le \!&\! 0 \\ \exp\!\big({\rm uxp}(z\!-\!1)\big) &{\rm at} &~ 0 \!&\! < \!&\! \Re(z) \!& \end{array} \right. \)
The sequence of vertical cutlines separate the complex plane to the set of almost iindependent strips, where the approximation is holomorphic. This cutting was one of motivations to build-up the real-holomorphic tetration tet.
Map f corresponds to the approximation \(\mathrm{Fit}_3\) constructed in the following way:
\(s_2(z)= \exp\!\Big(\exp(z-2.51)\Big)-0.6+0.08(z\!+\!1)\)
\(\mathrm{fit}_2(z) \!=\!\) \( \ln(2\!+\!z) + (1\!+\!z)\left( 1 + \frac{z}{2}\exp\!\Big((z\!-\!1)s_2(z)\Big) \Big(\!\mathrm e\! -2\! +\! \ln\frac{4}{3} \Big) - \ln 2 \right)\)
\(\mathrm{fit}_3(z)=0.6\!~\mathrm{fit}_{2}(z)+0.4\!~\ln\big( \mathrm{fit}_{2}(z+1)\big)\)
\(\mathrm{Fit}_3(z)= \left\{\!\! \begin{array}{ccccc cc} \ln\!\big({\rm Fit}_{3}(z\!+\!1)\big) &{~\rm at}&~ \!&\! \!&\! \Re(z) \!&\! \le \!&\! -1 \!\\ \mathrm{fit}_{3}(z) &{~\rm at}& -1 \!&\! < \!&\! \Re(z) \!&\! \le \!&\! 0 \!\\ \exp\!\big({\rm Fit}_{3}(z\!-\!1)\big) &{~\rm at}&~ 0 \!&\! < \!&\! \Re(z) \!& \end{array} \right.\)
Constants in definition of function \(s\) have rather historical than mathematical meaning, because they were used to guess the asymptotic behavior of tetration, while the precise algorithm for the evaluation had not yet been discovered. Using the precise implementation, the approxximation can be improved.
Map g corresponds to the asymptotic representation
\(f(z)=\mathrm{fit}_6(z) =\) \( \left\{ \begin{array} ~ L+\exp(kz+r) ~, ~ \Re(z)<-8\\ \exp\Big(\mathrm{fit}_6(z\!-\!1)\Big)~,~ \Re(z)\ge -8 \end{array} \right.\)
for \(\Im(z)>0.5\) and \(f(z)=\mathrm{fit}_6(z^*)^*\) for \(\Im(z)<0.5\) ; In the map, the strip of intermediate values \(|y|<1/2\) is left empty. In formula above, \(L\approx 0.31813150520476413 + 1.3372357014306895 \,\mathrm i\) is fixed point of logarithm, \(L=\ln(L)\). For Natural tetration, the increment \(k=L\). Parameter \(r\) provides the match of the two asymptotics. It is fundamental mathematical constant; \(r \approx 1.075820830781 - 0.9466419207254 \, \mathrm i\) . This precision seems to be sufficient for the applications; however, the improvement of the precision may be subject of the additional research.
Map h shows the precise implementation of tetration with 14 decimal digits through the Cauchi integral [1].
In principle, the approximations \(\mathrm{Fit}_3\), shown in map e, and \(\mathrm{Fit}_6\), shown in map f, allow to implement tetration in the whole complex plane with at least 3 defimal figures; this precision is sufficient to make camera–ready illustrations of properties of tetration. Historically, approximations \(\mathrm{fit}_6\) and \(\mathrm{Fit}_6\) were obtained after to implement the tetration through the Cauchi integral, when not only the limiting value \(L\) of tetration had been revealed, but also the exponential approaching of tetration to this value.
Numerical implementation
Up to date, the most reliable complex double implementation of natural tetration tet in C++ is loaded as fsexp.cin, and called FSEXP. This name happened to be not woo good, because the search engines for this name offer many cites that have nothing to do with super functions, exponentials, nor even mathematics. I hope, the improved implementation will have more suitable name.
Implementation of the corresponding arctetration is loaded as fslog.cin. The name of the routine, FSLOG, corresponds the the idea to name arctetration with identifier "super logarithm". The name Superlogarithm causes confusions, it makes an impression that it is superfunction of logarithm. One superfunction \(G\) of logarithm can be expressed through the tetration, namely, \(G(z)=\mathrm{tet}(-z)\), which is not arctetration. For this reason, the name "fslog" is not good. However, for the historic reason, the name of the routine remains. As soon as the most efficient algorithms for evaluation of tetration and arctetration will be implemented, the implementations may have more understandable names TET and ATE.
Fixed points and Superfunction
For natural tetration, the real fixed point \(L_{\mathrm e,4,0} \!=\! L_{\mathrm e, 4,0} \!\approx\! -1.8503545290271812\) is used to construct the superfunction of tetration, the fifth Ackermann function, called natural pentation;
\(\mathrm{pen}=A_{\mathrm e,5}\)
For pentation, the tetration tet is interpreted as the transfer function. Pentation satisfies the transfer equation
\(\mathrm{pen}(z\!+\!1)=\mathrm{tet}\Big(\mathrm{pen}(z)\Big)\)
Keywords
Ackermann function, Exponential, exp, Fixed point, fsexp.cin, fslog.cin, Superfunction, Tetration, Transfer equation,
References
- ↑ 1.0 1.1 1.2 1.3
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670. Cite error: Invalid<ref>tag; name "analuxp" defined multiple times with different content Cite error: Invalid<ref>tag; name "analuxp" defined multiple times with different content Cite error: Invalid<ref>tag; name "analuxp" defined multiple times with different content - ↑ http://www.ils.uec.ac.jp/~dima/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45.
- ↑ http://www.tandfonline.com/doi/full/10.1080/10652460500422247 M. H. Hooshmand, (2006). "Ultra power and ultra exponential functions". Integral Transforms and Special Functions 17 (8): 549–558. %doi:10.1080/10652460500422247.
http://www.springerlink.com/content/u7327836m2850246/ H.Trappmann, D.Kouznetsov. Uniqueness of Analytic Abel Functions in Absence of a Real Fixed Point. Aequationes Mathematicae, v.81, p.65-76 (2011)
http://link.springer.com/article/10.1007/s10444-017-9524-1 William Paulsen and Samuel Cowgill. Solving \(F(z+1)=b^{F(z)}\) in the complex plane. Advances in Computational Mathematics, 2017 March 7, p. 1–22