Difference between revisions of "Serega function"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | '''Serega function''' is nongolomorphic function |
+ | '''Serega function''' is nongolomorphic function \(\mathrm{Serega}\) of complex variable \(z\) such that |
| − | : |
+ | : \(F(z)=x+\mathrm i ~ \exp(\mathrm i ~ z^*)\) |
where the asterisk means the [[complex conjugation]]. |
where the asterisk means the [[complex conjugation]]. |
||
| Line 11: | Line 11: | ||
The coordinates of the particles of the liquid can be written in such a way: |
The coordinates of the particles of the liquid can be written in such a way: |
||
| − | : |
+ | : \( X=X(x,y,t)= \Re( \mathrm{Serega}( k x - \omega t + \mathrm i y))\) |
| − | : |
+ | : \( Y=Y(x,y,t)= \Im( \mathrm{Serega}( k x - \omega t + \mathrm i y))\) |
| − | where |
+ | where \(x\) and \(y\) determine the particle, while \(X\) and \(Y\) are Cartesian coordinates of the particle at time \(t\). |
| − | Parameter |
+ | Parameter \(k\) has sense of wavenymber. |
| − | Parameter |
+ | Parameter \(\omega\) has sense of frequency. |
| − | Particles with |
+ | Particles with \(y=y_s=\mathrm {constant}\) can be interpreted as surface of the liquid, at least while \(y<0\). |
The components of velocity |
The components of velocity |
||
| − | : |
+ | : \(u=\dot X=u(x,y,t)\) |
| − | : |
+ | : \(v=\dot Y=v(x,y,t)\) |
| − | are derivatives of functions |
+ | are derivatives of functions \(X\) and \(Y\) with respect to the last argument. |
| − | WIth the inverse function |
+ | WIth the inverse function \(\mathrm{ArcSerega}\), velocities can be expressed in terms of the Cartesian coordinates: |
| − | : |
+ | : \(U=U(x(X,Y,t), y(X,Y,t), t)=u(x,y,t)\) |
| − | : |
+ | : \(V=V(x(X,Y,t), y(X,Y,t), t)=v(x,y,t)\) |
where |
where |
||
| − | : |
+ | : \(x(X,Y,t)= \frac{1}{k}\left( -\omega t + \Re(\mathrm{ArcSerega} ( kX - \omega t +\mathrm i k Y )) \right)\) |
| − | : |
+ | : \(y(X,Y,t)= \frac{1}{k} \Im(\mathrm{ArcSerega} ( kX - \omega t +\mathrm i k Y ))\) |
These velocities satisfy the [[Navier-Stokes equation]] for the Eulerian liquid (without viscosity). The [[surface tension]] of the liquid is neglected. The liquid is treated as non–compressible. |
These velocities satisfy the [[Navier-Stokes equation]] for the Eulerian liquid (without viscosity). The [[surface tension]] of the liquid is neglected. The liquid is treated as non–compressible. |
||
| − | The gravitational force with acceleration |
+ | The gravitational force with acceleration \(g=\omega/k\) should be applied as the "external force". |
==ArcSerega== |
==ArcSerega== |
||
| Line 46: | Line 46: | ||
The Complex map of ArcSerega is shown in figure at right. ArcSerega is also non–holomorphic; therefore, the line of constant real part are not orthogonal to the lines of constant imaginary part. |
The Complex map of ArcSerega is shown in figure at right. ArcSerega is also non–holomorphic; therefore, the line of constant real part are not orthogonal to the lines of constant imaginary part. |
||
| − | ArcSerega is periodic with period |
+ | ArcSerega is periodic with period \(2\pi\) |
| − | ArcSerega is Symmetric with respect to the real part of argument: |
+ | ArcSerega is Symmetric with respect to the real part of argument: \(\mathrm{ArcSerega}(X+\mathrm i Y) = \mathrm{ArcSerega}(-X+\mathrm i Y)\) |
At large positive values of the imaginary part of the argument, ArcSerega behaves in a way, similar to logarithm. Usually such a range of values is not used in the applications, and the part of the complex map above the cycloid |
At large positive values of the imaginary part of the argument, ArcSerega behaves in a way, similar to logarithm. Usually such a range of values is not used in the applications, and the part of the complex map above the cycloid |
||
| − | + | \(X+\mathrm i Y=a-\sin(a) + \mathrm i \cos(a)\), \(a\in \mathbb R\) is left empty at the figure. |
|
==Ethimology== |
==Ethimology== |
||
Latest revision as of 18:25, 30 July 2019
Serega function is nongolomorphic function \(\mathrm{Serega}\) of complex variable \(z\) such that
- \(F(z)=x+\mathrm i ~ \exp(\mathrm i ~ z^*)\)
where the asterisk means the complex conjugation.
The Serega function is not holomorphic, and, therefore, not differentiable, id est, the derivative depends on the direction of variation of the argument. However, the derivatives with respect to real and imaginary parts of the argument exist.
Appearance
In the Fluid mechanics, the Serega function describes transfer from the Euler coordinates to the Lagrangian coordinates for the movement of the surface waves of an idealized liquid. The real and imaginary parts of the argument have sense of the labels of the particles of the liquid while the real and imaginary parts of the value have sense of the Cartesian coordinates of the liquid.
The coordinates of the particles of the liquid can be written in such a way:
- \( X=X(x,y,t)= \Re( \mathrm{Serega}( k x - \omega t + \mathrm i y))\)
- \( Y=Y(x,y,t)= \Im( \mathrm{Serega}( k x - \omega t + \mathrm i y))\)
where \(x\) and \(y\) determine the particle, while \(X\) and \(Y\) are Cartesian coordinates of the particle at time \(t\).
Parameter \(k\) has sense of wavenymber.
Parameter \(\omega\) has sense of frequency.
Particles with \(y=y_s=\mathrm {constant}\) can be interpreted as surface of the liquid, at least while \(y<0\).
The components of velocity
- \(u=\dot X=u(x,y,t)\)
- \(v=\dot Y=v(x,y,t)\)
are derivatives of functions \(X\) and \(Y\) with respect to the last argument.
WIth the inverse function \(\mathrm{ArcSerega}\), velocities can be expressed in terms of the Cartesian coordinates:
- \(U=U(x(X,Y,t), y(X,Y,t), t)=u(x,y,t)\)
- \(V=V(x(X,Y,t), y(X,Y,t), t)=v(x,y,t)\)
where
- \(x(X,Y,t)= \frac{1}{k}\left( -\omega t + \Re(\mathrm{ArcSerega} ( kX - \omega t +\mathrm i k Y )) \right)\)
- \(y(X,Y,t)= \frac{1}{k} \Im(\mathrm{ArcSerega} ( kX - \omega t +\mathrm i k Y ))\)
These velocities satisfy the Navier-Stokes equation for the Eulerian liquid (without viscosity). The surface tension of the liquid is neglected. The liquid is treated as non–compressible. The gravitational force with acceleration \(g=\omega/k\) should be applied as the "external force".
ArcSerega
While Serega function is not holomorphic, the inversion is not so easy as inversion of factorial or tetration, and ArcSerega cannot be approximated inverting the power series of Serega. In the implementation of ArcSerega, it is treated as pair of functions of pair of variables.
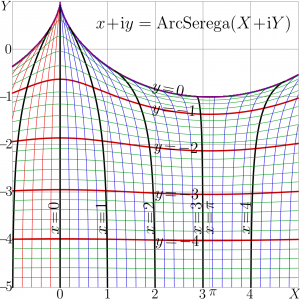
The Complex map of ArcSerega is shown in figure at right. ArcSerega is also non–holomorphic; therefore, the line of constant real part are not orthogonal to the lines of constant imaginary part.
ArcSerega is periodic with period \(2\pi\)
ArcSerega is Symmetric with respect to the real part of argument: \(\mathrm{ArcSerega}(X+\mathrm i Y) = \mathrm{ArcSerega}(-X+\mathrm i Y)\)
At large positive values of the imaginary part of the argument, ArcSerega behaves in a way, similar to logarithm. Usually such a range of values is not used in the applications, and the part of the complex map above the cycloid \(X+\mathrm i Y=a-\sin(a) + \mathrm i \cos(a)\), \(a\in \mathbb R\) is left empty at the figure.
Ethimology
The identifier of the Serega function is chosen as slightly modified first name of Sergey Kuznetsov, who thinks, that in the idealized wave, the movement is rotorless. [1].
The Serega function is expected to be useful in analysis of the break of waves, as the important basis function to approximate more complicated solutions of the Navier-Stokes with appropriate combinations of the Serega functions
Keywords
Navier-Stokes equation, Sergey Kuznetsov, Fluid dynamics
References
- ↑ Sergey Kuznetsov. Private communication, Sep 1, 2012 at 5:34 PM .. Пена на гребне морских волн появляется по двум возможным причинам - из-за нелинейной перекачки энергии в высшие гармоники (их и видно как рябь) ускорение в гребне становится больше g или скорость частиц воды становится больше фазовой скорости "волны в целом". Никаких вихрей для объяснения обрушения не требуется, вихри образуются после начала обрушения и на основные процессы нелинейной трансформации волн влияния непосредственного не оказывают, а лишь дисссипируют энергию более-менее равномерно по спектру.