Difference between revisions of "Shoka function"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| Line 1: | Line 1: | ||
| − | [[File:ShokaMapT.png|400px|thumb| |
+ | [[File:ShokaMapT.png|400px|thumb|\(u\!+\!\mathrm i v = \mathrm{Shoka}(x\!+\mathrm i y)\) ]] |
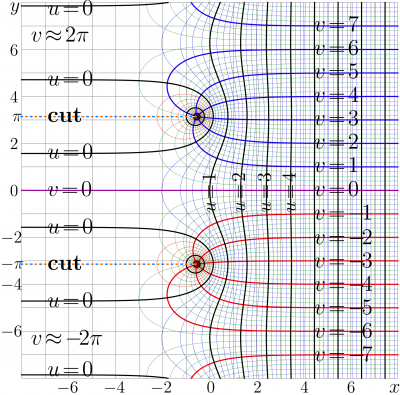
[[Shoka function]] is holomorphic function, |
[[Shoka function]] is holomorphic function, |
||
| − | : |
+ | :\( \mathrm{Shoka}(z)=z+\ln\!\Big( \exp(-z) +\mathrm e -1\Big)\) |
[[Complex map]] of the [[Shoka function]] is shown in figure at right. |
[[Complex map]] of the [[Shoka function]] is shown in figure at right. |
||
| Line 8: | Line 8: | ||
==Range of holomorphizm== |
==Range of holomorphizm== |
||
The [[Shoka function]] is holomorphic at the complex plane with cuts |
The [[Shoka function]] is holomorphic at the complex plane with cuts |
||
| − | : |
+ | : \( x+ (1\!+\!2n) \mathrm i \pi ~\) at real \(x\) and integer \(n\). |
In such a way, the countable set of cut lines are directed to the left. |
In such a way, the countable set of cut lines are directed to the left. |
||
==Inverse function== |
==Inverse function== |
||
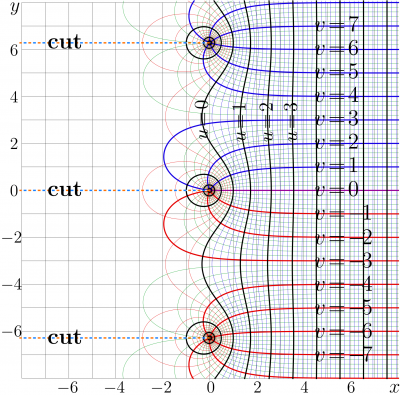
| − | [[File:ArcShokaMapT.png|400px|thumb| |
+ | [[File:ArcShokaMapT.png|400px|thumb| \(u\!+\!\mathrm i v= \mathrm{ArcShoka}(x\!+\!\mathrm i y)\) ]] |
| − | The [[inverse function]] |
+ | The [[inverse function]] \(\mathrm{ArcShoka}=\mathrm{Shoka}^{-1}\) can be expressed as elementary function; for \(|\Im(z)| < \pi\), |
| − | : |
+ | : \(\displaystyle \mathrm{ArcShoka}(z)= z + \ln \!\left( \frac{1\!-\!\mathrm e^{-z}}{\mathrm e \!-\!1} \right)\) |
Some properties of the inverse function are collected in the special article [[ArcShoka]]. |
Some properties of the inverse function are collected in the special article [[ArcShoka]]. |
||
| Line 21: | Line 21: | ||
Complex maps of Shoka and ArcShoka look similar. The following relation takes place: |
Complex maps of Shoka and ArcShoka look similar. The following relation takes place: |
||
| − | + | \(\mathrm{ArcShoka}(z)=\mathrm{Shoka}\big(z-\ln(\mathrm e\! -\!1) - \mathrm i \pi\big) -\ln(\mathrm e\!-\!1) +\mathrm i \pi\) |
|
that can be verified with the direct substitution. |
that can be verified with the direct substitution. |
||
| Line 27: | Line 27: | ||
==Shoko function== |
==Shoko function== |
||
In vicinity of the real axis, the [[Shoka function]] coincides with the [[Shoko function]], |
In vicinity of the real axis, the [[Shoka function]] coincides with the [[Shoko function]], |
||
| − | : |
+ | :\( \mathrm{Shoko}(z) = \ln\!\Big( 1+ \exp(z)(\mathrm e -1)\Big)\) |
| − | However, the cut lines of the [[Shoko function]] are directed to the right, and the [[Shoko function]] is periodic with period |
+ | However, the cut lines of the [[Shoko function]] are directed to the right, and the [[Shoko function]] is periodic with period \(P=2 \pi \mathrm i\). |
==Applications in Laser science== |
==Applications in Laser science== |
||
Revision as of 18:27, 30 July 2019
Shoka function is holomorphic function,
- \( \mathrm{Shoka}(z)=z+\ln\!\Big( \exp(-z) +\mathrm e -1\Big)\)
Complex map of the Shoka function is shown in figure at right.
Contents
Range of holomorphizm
The Shoka function is holomorphic at the complex plane with cuts
- \( x+ (1\!+\!2n) \mathrm i \pi ~\) at real \(x\) and integer \(n\).
In such a way, the countable set of cut lines are directed to the left.
Inverse function
The inverse function \(\mathrm{ArcShoka}=\mathrm{Shoka}^{-1}\) can be expressed as elementary function; for \(|\Im(z)| < \pi\),
- \(\displaystyle \mathrm{ArcShoka}(z)= z + \ln \!\left( \frac{1\!-\!\mathrm e^{-z}}{\mathrm e \!-\!1} \right)\)
Some properties of the inverse function are collected in the special article ArcShoka.
Complex maps of Shoka and ArcShoka look similar. The following relation takes place:
\(\mathrm{ArcShoka}(z)=\mathrm{Shoka}\big(z-\ln(\mathrm e\! -\!1) - \mathrm i \pi\big) -\ln(\mathrm e\!-\!1) +\mathrm i \pi\)
that can be verified with the direct substitution.
Shoko function
In vicinity of the real axis, the Shoka function coincides with the Shoko function,
- \( \mathrm{Shoko}(z) = \ln\!\Big( 1+ \exp(z)(\mathrm e -1)\Big)\)
However, the cut lines of the Shoko function are directed to the right, and the Shoko function is periodic with period \(P=2 \pi \mathrm i\).
Applications in Laser science
As the Shoko function, the Shoka function is superfunction of the Keller function and describes the evolution of the short pulse of light in a two-level laser medium. Properties and expansions of the Shoka function are similar to those of the Shoko function and are not repeated here.
Tania function
The Shoka function behaves similar to the Tania function, but have countable set of cutlines in the left hand side of the complex plane, while the Tania funciton has only two cut lines.
Origin of the name
Initially, the Shoko function had been implemented; that function is named after Shoko san. Then in happened, that the cut lines of the Shoko function go to the right hand side direction, that makes difficult its comparison with the Tania function in the complex plane. Name Shoka function is created as small modification of name Shoko function.
References
Keywords
Shoko function, Keller function, Superfunction, Laser science