Difference between revisions of "SuFac"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| Line 5: | Line 5: | ||
Д.Кузнецов. Суперфункции. [[Lambert Academic Publishing]], 2014. |
Д.Кузнецов. Суперфункции. [[Lambert Academic Publishing]], 2014. |
||
</ref>]] |
</ref>]] |
||
| − | [[SuFac]], or super factorial, is [[superfunction]] of [[Factorial]] constructed with [[regular iteration]] at the fixed point |
+ | [[SuFac]], or super factorial, is [[superfunction]] of [[Factorial]] constructed with [[regular iteration]] at the fixed point \(L\!=\!2\) with additional condition \(\mathrm{suFac}(0)\!=\!3\). |
| − | Explicit plot |
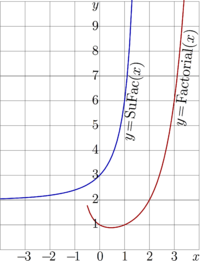
+ | Explicit plot \(y\!=\!\mathrm{SuFac}(x)\) is shown in figure at right with blue curve in comparison with graphic of [[factorial]], \(y\!=\!\mathrm{Factorial}(x)\), shown with red line. |
The numerical implementation in [[C++]] of SuFac is loaded as [[sufac.cin]]. |
The numerical implementation in [[C++]] of SuFac is loaded as [[sufac.cin]]. |
||
Latest revision as of 18:48, 30 July 2019
SuFac, or super factorial, is superfunction of Factorial constructed with regular iteration at the fixed point \(L\!=\!2\) with additional condition \(\mathrm{suFac}(0)\!=\!3\).
Explicit plot \(y\!=\!\mathrm{SuFac}(x)\) is shown in figure at right with blue curve in comparison with graphic of factorial, \(y\!=\!\mathrm{Factorial}(x)\), shown with red line.
The numerical implementation in C++ of SuFac is loaded as sufac.cin.
References
http://www.springerlink.com/content/qt31671237421111/fulltext.pdf?page=1
http://www.ils.uec.ac.jp/~dima/PAPERS/2010superfae.pdf
http://mizugadro.mydns.jp/PAPERS/2010superfae.pdf
D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12.
http://mizugadro.mydns.jp/PAPERS/2010superfar.pdf Д,Кузнецов, Г.Траппманн. Суперфункции и корень их факториала. Вестник Московского Университета, серия 3, 2010, стр.8-14)