SuNem

$y\!=\!\mathrm{SuNem}_{q}(x)$ for various $q$

$u\!+\!\mathrm i v=\mathrm{SuNem}_{0}(x\!+\!\mathrm i y)$

$u\!+\!\mathrm i v=\mathrm{SuNem}_{1}(x\!+\!\mathrm i y)$

$u\!+\!\mathrm i v=\mathrm{SuNem}_{2}(x\!+\!\mathrm i y)$

SuNem is superfunction for the Nemtsov function

$\mathrm{Nem}_{q}(z)=z+z^3+qz^4$

It is assumed, that $q\!>\!0$, although the formula can be used for some other values of the parameters too.

SuNem is specific solution of the transfer equation

$\mathrm{Nem}_{q}\big( \mathrm{SuNem}_{q}(z)\big)=\mathrm{SuNem}_{q}(z\!+\!1)$.

It is assumed that $\mathrm{SuNem}_{q}(0)=1$.

Also, the specific asymptotic behaviour at infinity is assumed,

$\mathrm{SuNem}_{q}(z) = {\displaystyle \frac{1}{\sqrt{-2z}}}\left(1+O\left(\frac{1}{\sqrt{-2z}} \right)\right)$

for any fixed phase $\mathrm{Arg}(z)$ different from zero.

For any $\varepsilon>0$, the formula is valid for any large $|z|$ such that $|\mathrm{Arg}(z)|>\varepsilon$.

Along the real axis, SuNem shows fast growth from zero at $-\infty$ to plus infinity at $+\infty$.

Asymptotic expansion

Function SuNem is constructed by its asymptotical expansion.

For the superfunction $F$ of the Nemtsov transfer function $T=\mathrm{Nem}_{q}$, it can be obtained from the transfer equation

$T(F(z))=F(z+1)$

Keping some positive integer mumber $M$ of terms, the asymptotic solution can be written as follows:

$\displaystyle \tilde F(z) = \frac{1}{\sqrt{-2z}} \left(1+ \frac{P_m(\ln(-z))} {(-2z)^{m/2}} \right)$

where $\displaystyle P_m(z)=\sum_{n=0}^{\mathrm{IntegerPart}(m/2)} A[m,n]\, z^m$

Substitution of $\tilde F$ into the transfer equation gives the coefficients $A$. These coefficients can be calculated with the mathematica code below:

Mathematica generator of the algorithm

The first 18 terms of the asymptotic representation of super function $F$ can be computed with Mathematica software, using the code below:

T[z_]=z+z^3+q z^4
P[m_, L_] := Sum[a[m, n] L^n, {n, 0, IntegerPart[m/2]}]
a[1, 0] = -q; a[2, 0] = 0;
m = 2;
F[m_,z_] = (-2 z)^(-1/2) (1 + Sum[P[n, Log[-z]]/(-2 z)^(n/2), {n, 1, 2}]);
s[m]=Numerator[Normal[Series[(T[F[m,-1/x^2]] - F[m,-1/x^2+1]) 2^((m+1)/2)/x^(m+3), {x,0,0}]]]
sub[m] = Extract[Solve[s[m]==0, a[m,1]], 1];
SUB[m] = sub[m]

For[m = 3, m < 18,
 F[m, z_] = ReplaceAll[(-2 z)^(-1/2) (1+Sum[P[n, Log[-z]]/(-2 z)^(n/2), {n,1,m}]), SUB[m-1]];
 s[m] = Numerator[Normal[Series[(T[F[m,-1/x^2]]-F[m,-1/x^2+1]) 2^((m+1)/2)/x^(m+3),{x,0,0}]]];
  t[m] = Collect[Numerator[ReplaceAll[s[m], Log[x] -> L]], L];
  u[m] = Table[
    Coefficient[t[m] L, L^n] == 0, {n, 1, 1 + IntegerPart[m/2]}];
  tab[m] = Table[a[m, n], {n, 0, IntegerPart[m/2]}];
  Print[sub[m] = Simplify[Extract[Solve[u[m], tab[m]], 1]]];
  SUB[m] = Join[SUB[m - 1], sub[m]];
  m++];

For[m=1, m<18,
  For[n=0,n<(m+1)/2,
     A[m, n] = TeXForm[ReplaceAll[a[m, n], sub[m]]];
     Print["APQ[", m, "][", n, "]=", A[m, n], ";"]
   n++];
m++];

Evaluation of superfunction

$y\!=\!\mathrm{SuNe}_q(x)$ for $q=-1, -0.5, 0, 0.5, 1, 2, 3$

displacement $x_0$ versus parameter $q$

First, the superfunction of the Nemtsov function is constructed, that does not satisfy the requirement on its value at zero. The idea is to use the asymptotival expansion $\tilde F$ of the superfunction in the area, where it provides the good approximation, displacing the argument of superfunction into this area with using of the transfer equation.

Superfunction $\mathrm{SuNe}_q$ of the Nemtsov function $\mathrm{Nem}_q$ appears as limit

$\displaystyle \mathrm{SuNe}_q(z)=\lim_{n \rightarrow \infty} \mathrm{Nem}_q^{\,n} (\tilde F(z\!-\!n))$

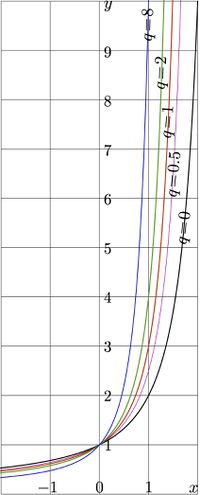
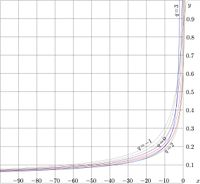
Explicit plot of function $\mathrm{SuNe}_q$ is shown in figure at right for $q=-1, -0.5, 0, 0.5, 1, 2, 3~$. Then, function SuNem appears with the appropriate displacement of the argument:

$\mathrm{SuNem}_q(z)=\mathrm{SuNe}_q(x_0(q)+z)$

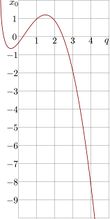
where displacement $x_0=x_0(q)$ is real solution of equation $F_q(x_0)\!=\!1$. This solution is shown in figure at left. In order to show the general trend of function $x_0$, the graphic is extended a little bit into the range of negative $q$.

Inverse function

Inverse function of SuNem is function AuNem, that is Abel function of the Nemtsov function; in wide range of values of $z$, it satisfies the Abel equation

$\mathrm{AuNem_{q}} \big( \mathrm{Nem_{q}}(z)\big) = \mathrm{Nem_{q}}(z\!+\!1)$

Iterates of the Nemtsov function

With functions SuNem and AuNem, the iterates of the Nemtsov function can be written as usually:

$\mathrm{Nem}^n(z)=\mathrm{SuNem}(n+\mathrm{AuNem}(z))$

Keywords

AuNem, Book, Exotic iterate, Nemtsov function, SuNem, Superfunction