SuPow
SuPow is specific superpower function, id est, the superfunction of the power function $~z\mapsto z^a\!=\!\exp(\ln(z) \,a)~$
For given parameter $a$,
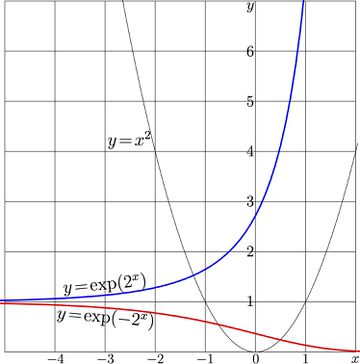
$\mathrm{SuPow}_a(z)=\exp(a^z)$
Usually, it is assumed, that $a\!>\!1$.
Contents
Transfer function
Function $F\!=\!\mathrm{SuPow}_a$ is superfunction for the specific power function $T(z)\!=\!z^a$. The superfunction satisfies the transfer equation
$T(F(z))=F(z\!+\!1)$
another solution is denoted as SdPow;
$\mathrm{SdPow}_a(z)=\exp(-a^z)$
For $a\!=\!2$ graphics $y=T(x)$, $y=\mathrm{SuPow}_2(x)$ and $y=\mathrm{SdPow}_2(x)$ are shown in Fig.1.
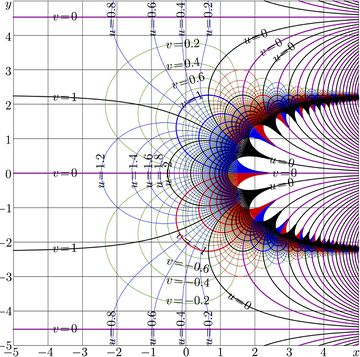
For $a\!=\!2$, complex map of function $\mathrm{SuPow}_a$ is shown in Fig.2.
SuPow and SdPow
Function $\mathrm{SuPow}_a$ is periodic, as well as function $\mathrm{SdPow}_a$
The period $P=2\pi\mathrm i / \ln(a)$ is the same for both these functions.
For $a\!>\!1$, the period is pure imaginary. A little bit more than one period fits the range of map in Fig.2.
Such a periodicity is typical for a superfunction of a transfer function with a real fixed point. Some of thiese function are listed in the Table of superfunctions.
Functions SuPow and SdPow are related with expression
$\mathrm{SuPow}_a(z)=\mathrm{SdPow}_a(z\!+\!P/2)$
Similar relations hold also for many other pairs of periodic superfunctions of some transfer function with two fixed points
However, namely the superpower functions have also the specific relation,
$\displaystyle \mathrm{SuPow}_a(z)=\frac{1}{\mathrm{SdPow}_a(z)}$
Inverse function
The inverse function AuPow$=\mathrm{SuPow}^{-1}$ is also elementary function;
$\mathrm{AuPow}_a(z)=\log_a(\ln(z))$
AuPow is the Abel function for the same transfer function $T(z)=z^a$ and satisfies the Abel equation
$\mathrm{AuPow}_a(z^a)=\mathrm{AuPow}_a(z)+1$
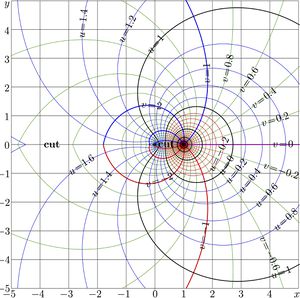
Complex map of function $\mathrm{AuPow}_2$ is shown in figure at right.
For $a\!>\!1$, function $\mathrm{AuPow}_2$ has cut line along the real axis from $1$ to $-\infty$.
Application
References
Keywords
AuPow, Book, Power function, SdPow, Superfunction, Superfunctions, Superpower