SuTra
SuTra, or SuperTrappmann function is superfunction of the Trappmann function, $~\mathrm{tra}(z)=z+\exp(z)~$
The Trappmann function is treated as the transfer function; and the SuTra function, as superfunction of tra, satisfies the transfer equation
(1) $~ ~ ~ \mathrm{SuTra}(z\!+\!1) = \mathrm{tra}\Big( \mathrm{SuTra}(z)\Big)$
In orfer to narrow the set of solutions, it is assumed, that
(2) $~ ~ ~ \mathrm{SuTra}(z^*) = \mathrm{SuTra}(z)^* ~ ~$, $~ ~ ~ \mathrm{SuTra}(0) = 0 $
and that SuTra is entire function. Also, the logarithmic asymptotic bahavior at infinity is assumed, at least outside the strip
(3) $~ ~ ~ \{ z\in \mathbb Z : \Re(z)\!>\!2, |\Im(z)|\!<\!2 \}$
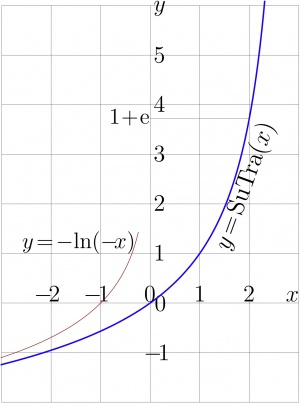
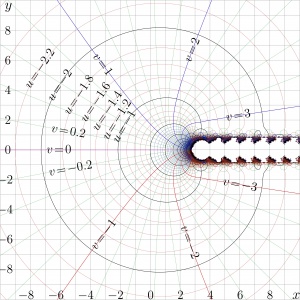
Function SuTra is expected to be the only function with such a behavior. The plot of the SuTra is shown in Figure 1. For comparison, its asymptotic $~u\!=\!-\!\ln(-x)~$ is shown with thin line. The complex map of the SuTra is shown in Figure 2.
History
The Trappmann function, $~\mathrm{tra}(z)=z+\exp(z)~$, had been suggested in 2011 by Henryk Trappmann as an example of a transfer function, for which it is difficult to construct the superfunction. For this reason, the Trappmann function is called after his name.
However, the superfunction of the Trappmann function, id est, SuTra can be expressed through that of the function zex, $~\mathrm{zex}(z)=\mathrm{ArcLambertW}(z)=z\,\exp(z)$, in the following way:
(4) $~ ~ ~ \mathrm{SuTra}(z)=\ln\Big( \mathrm{SuZex}(z)\Big)$
at least for $z$ outside the strip (3). Perhaps, the similar representation could be used also for values inside that strip with appropriate choice of branch of the logarithmic function. Practically, it is easier to use the transfer equation (1) recurrently, bringing the argument of SuTra to the range there the representation (4) is valid. In such a way function SuTra is implemented in the C++ algorithm SuTra.cin for plotting of the complex map in Figure 1.
Iteration of the Trappmann function
The Trappmann function is important example of function without fixed points. Such functions were expected to be difficult for construction of the fractional iterates. However, due to expression (4), the iterates of the Trappmann function can be expressed with general formula
(5) $~ ~ ~ \mathrm{Tra}^n(z)=\mathrm{SuTra}\Big( n+ \mathrm{AuTra}(z)\Big)$
where AuTra$\,=\!\mathrm{SuTra}^{-1}$ is the Abel function for the Trappmann function; the number $n$ of iteration in expression (5) has no need to be integer. As usually, the superfunction can be iterated any real (can even complex) number of times.
In certain range of values of the argument, and, in particular, along the real axis, The Abel–Trappmann function AuTra can be expressed through the Abel function of zex, id est, through AuZex in the following way:
(6) $~ ~ ~ \mathrm{AuTra}(z)=\mathrm{AuZex}\Big(\exp(z)\Big)$
Representations (6) and (5) are used to plot graphics of the non–integer iterates of the Trappmann function.
References
Keywords
Trappmann function, SuperFunction, Zex, SuZex, AuTra, Iteration