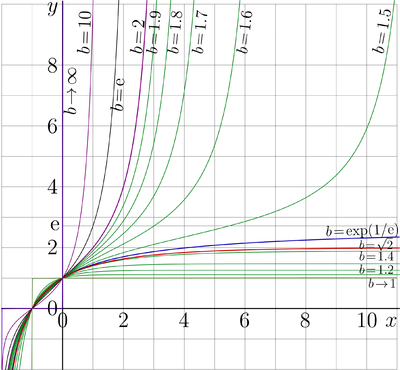
Difference between revisions of "Tetration"
(→Keywords) |
(→Case \(b\!=\! \mathrm{e}\)) |
||
| (12 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | [[File:Tetreal10bx10d.png|400px|right|thumb| |
+ | [[File:Tetreal10bx10d.png|400px|right|thumb|\(y={\rm tet}_b(x)~~\) versus \(x\) for various \(b\)]] |
| − | <!-- [[File:Tet10bxr.png|600px|right|thumb| |
+ | <!-- [[File:Tet10bxr.png|600px|right|thumb|\(y={\rm tet}_b(x)\) versus \(x\) for various \(b\).]] !--> |
<!-- |
<!-- |
||
| − | [[File:Tetreal2215.jpg|400px|thumb| |
+ | [[File:Tetreal2215.jpg|400px|thumb|\(f={\rm tet}_b(x)\) in the \(x,b~\) plane shown with levels \(f= \rm const\).]] !--> |
[[File:Ackerplot.jpg|400px|thumb|Tetration to base e (dashed) compared to other [[Ackermann function]]s]] |
[[File:Ackerplot.jpg|400px|thumb|Tetration to base e (dashed) compared to other [[Ackermann function]]s]] |
||
| − | '''Tetration''' (or Tetrational) |
+ | '''Tetration''' (or Tetrational) \({\rm tet}_b\) to base \(b \in \mathbb R\), \(b\!>1\)<br> |
| − | is the |
+ | is the \(\mathbb C \mapsto \mathbb C\) function, which is solution of equations |
| − | : |
+ | : \({\rm tet}_b(z\!+\!1) = \exp_b\!\big( {\rm tet}_b(z) \big)\) |
| − | : |
+ | : \({\rm tet}_b(0) = 1\) |
| − | such that, at least for |
+ | such that, at least for \(b\!>\!1\), is holomorphic at least in \(\{ z \in \mathbb C : \Re(z)\!>\!-2\}\). |
| − | Parameter |
+ | Parameter \(b\) is called "base", as in the cases of [[exponential]] and [[logarithm]]. According to the first of equations above, \(\mathrm{tet}_b\) is [[superfunction]] of [[exponential]] to base \(b\). Exponential is [[transfer function]] of tetration. |
| − | For real |
+ | For real \(b\), it is assumed that \({\rm tet}_b(z^*)={\rm tet}_b(z)^*\), where the asterisk means the complex conjugation. For the case of base \(b \!=\! \mathrm e\), the index may be omitted (as in the case of exp and logarithm), id est, \({\rm tet}(z)={\rm tet}_{\rm e}(z)\). The solution is believed to exist and to be unique, although the question about holomorphism with respect to base \(b\) |
| + | needs to be analyzed. |
||
| + | <!-- not all mathematicians agree that the proof of the existence and the uniqueness is rigorous.!--> |
||
| + | |||
| − | Case of complex values of $b$ is under investigation; conditions, that make the solution of equations above unique, may have need to be reformulated. |
||
| + | Case of complex values of \(b\) is under investigation; conditions, that make the solution of equations above unique, may have need to be reformulated. |
||
==Tetration as superfunction== |
==Tetration as superfunction== |
||
| − | + | Tetration is [[superfunction]] of [[exponential]]. Tetration can be interpreted as iterated exponential applied to unity. In the language [[Mathematica]], there already exists the special notation for the superfunction, id est, the function '''Nest'''. In particular, |
|
| − | + | \({\rm tet}(z)={\rm Nest}[\exp,1,z]\) . |
|
Up to year 2011, '''Nest''' is implemented only for the integer values of the last argument; the use with any expression, different from an integer constant, causes the error message. |
Up to year 2011, '''Nest''' is implemented only for the integer values of the last argument; the use with any expression, different from an integer constant, causes the error message. |
||
| − | For the beginning of year 2011, the tetration has been analyzed mainly for the real values of base |
+ | For the beginning of year 2011, the tetration has been analyzed mainly for the real values of base \(b \! > \! 1\). |
The different algorithms are used for the evaluation at |
The different algorithms are used for the evaluation at |
||
| − | + | \(1 \! < \! b \! < \! \exp(1/\rm e)\) |
|
<ref name="sqrt2"> |
<ref name="sqrt2"> |
||
http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html <br> |
http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html <br> |
||
| Line 32: | Line 35: | ||
</ref>, |
</ref>, |
||
| − | + | \(b \! = \! \exp(1/\rm e)\approx 1.44\) |
|
<ref name="e1e"> |
<ref name="e1e"> |
||
http://www.ams.org/journals/mcom/0000-000-00/S0025-5718-2012-02590-7/S0025-5718-2012-02590-7.pdf <br> |
http://www.ams.org/journals/mcom/0000-000-00/S0025-5718-2012-02590-7/S0025-5718-2012-02590-7.pdf <br> |
||
| Line 40: | Line 43: | ||
and for |
and for |
||
| − | + | \(b \! >\! \exp(1/\rm e)\) |
|
<ref name="moc1"> |
<ref name="moc1"> |
||
| − | http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html D.Kouznetsov. (2009). Solutions of |
+ | http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html D.Kouznetsov. (2009). Solutions of \(F(z+1)=\exp(F(z))\) in the complex plane.. Mathematics of Computation, 78: 1647-1670. DOI:10.1090/S0025-5718-09-02188-7. </ref><ref name="vladi"> |
http://www.ils.uec.ac.jp/~dima/PAPERS/2010vladie.pdf |
http://www.ils.uec.ac.jp/~dima/PAPERS/2010vladie.pdf |
||
D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45. |
D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45. |
||
| Line 49: | Line 52: | ||
H.Trappmann, D.Kouznetsov. Uniqueness of Analytic Abel Functions in Absence of a Real Fixed Point. Aequationes Mathematicae, v.81, p.65-76 (2011)</ref>. |
H.Trappmann, D.Kouznetsov. Uniqueness of Analytic Abel Functions in Absence of a Real Fixed Point. Aequationes Mathematicae, v.81, p.65-76 (2011)</ref>. |
||
| − | Therefore, one could expect some peculiarity of |
+ | Therefore, one could expect some peculiarity of \({\rm tet}_b(z)\) at |
| − | + | \(b\!=\!\exp(1/\rm e)\). |
|
| − | On the other hand, the plots of this function look smooth; one might expect that at a fixed value of |
+ | On the other hand, the plots of this function look smooth; one might expect that at a fixed value of \(z\), \({\rm tet}_b(z)\) is [[holomorphic]] (analytic) with respect to \(b\), and, in particular, in vicinity of \(b \! \approx \! \exp(1/\rm e)\). However, the visual smoothness at the real values of \(b\) can substitute neither the investigation of the analytic properties for complex \(b\) nor the mathematical proof of [[holomorphizm]]. |
| − | ==Behavior at |
+ | ==Behavior at \(1\!<\!b\!<\exp(1/{\rm e})\)== |
| − | At |
+ | At \(1\!<\!b\!<\exp(1/{\rm e})\), tetration is [[superfunction]] constructed with [[regular iteration]] at smallest of the real [[fixed point]]s \(L\!=\!L_1\), \(L\!=\!L_2\) of \(\log_b\). |
In language [[Mathematica]], the value of the fixed point can be expressed with function ProductLog, |
In language [[Mathematica]], the value of the fixed point can be expressed with function ProductLog, |
||
| − | : |
+ | : \(L_1(b)=-(\mathrm{ProductLog}[- \mathrm{Log}[b]]/\mathrm{Log}[b])\). |
The tetration is [[periodic function]]; the period |
The tetration is [[periodic function]]; the period |
||
| − | : |
+ | : \(T=\frac{2\pi \mathrm i} {\ln(L \, \ln(b))} \) |
| − | is pure imaginary. The cut line |
+ | is pure imaginary. The cut line \(\{x \in \mathbb R: x\le -2\}\) is reproduced at the translations along the imaginary axis. |
| − | + | \(\mathrm{tet}_b(x)\) remains real at \(x>-2\). It has logarithmic singularity at \(x=-2\), and it is [[monotonous function}monotonous]]ly grows at |
|
| − | + | \(x>-2\). |
|
| − | The tetration approaches its fixed point |
+ | The tetration approaches its fixed point \(L_1=L_1(b)\) at large values of the real part of its argument (and, in particular, along the real axis). |
| − | ==Evaluation and behavior at |
+ | ==Evaluation and behavior at \(b\!=\! \exp(1/{\rm e})\)== |
| − | For base |
+ | For base \(b\!=\!\exp(1/{\rm e})\! \approx\! 1.44\), the standard [[regular iteration]] should be modified. |
In partucular, the "new expansion" |
In partucular, the "new expansion" |
||
| − | <ref name="e1e" |
+ | <ref name="e1e"/> is suggested: |
| − | : |
+ | : \(\displaystyle |
F(z)=\mathrm e\cdot\left(1-\frac{2}{z}\left( |
F(z)=\mathrm e\cdot\left(1-\frac{2}{z}\left( |
||
1+\sum_{m=1}^{M} \frac{P_{m}\big(-\ln(\pm z) \big)}{(3z)^m} |
1+\sum_{m=1}^{M} \frac{P_{m}\big(-\ln(\pm z) \big)}{(3z)^m} |
||
| − | +\mathcal{O}\!\left(\frac{|\ln(z)|^{ |
+ | +\mathcal{O}\!\left(\frac{|\ln(z)|^{M+1}}{z^{M+1}}\right) |
| − | \right) \right) |
+ | \right) \right) \) |
where |
where |
||
| − | : |
+ | : \(\displaystyle P_{m}(t)=\sum_{n=0}^{m} ~c_{n,m~}~ t^n\) |
| − | The substitution of into equation |
+ | The substitution of into equation \(~ F(z\!+\!1)\!=\!\exp(F(z)/\mathrm e)~\) |
| − | and the asymptotic analysis with small parameter |
+ | and the asymptotic analysis with small parameter \(|1/z|\) determines |
| − | the coefficients |
+ | the coefficients \(c\) in the polynomials above. In particular, |
| − | : |
+ | : \( \begin{array}{ccc} |
P_{1}(t)&=&t \\ |
P_{1}(t)&=&t \\ |
||
P_{2}(t)&=&t^{2}+t+1/2 \\ |
P_{2}(t)&=&t^{2}+t+1/2 \\ |
||
| Line 90: | Line 93: | ||
P_{4}(t)&=&t^{4}+\frac{13}{ 3}t^{3}+\frac{ 45}{6}t^{2}+\frac{53}{10}t +\frac{ 67}{60} \\ |
P_{4}(t)&=&t^{4}+\frac{13}{ 3}t^{3}+\frac{ 45}{6}t^{2}+\frac{53}{10}t +\frac{ 67}{60} \\ |
||
P_{5}(t)&=&t^{5}+\frac{77}{12}t^{4}+\frac{101}{6}t^{3}+\frac{83}{ 4}t^{2}+\frac{653}{60}t+\frac{2701}{1680} |
P_{5}(t)&=&t^{5}+\frac{77}{12}t^{4}+\frac{101}{6}t^{3}+\frac{83}{ 4}t^{2}+\frac{653}{60}t+\frac{2701}{1680} |
||
| − | \end{array} |
+ | \end{array} \) |
| − | The evaluation with 9 polynomials |
+ | The evaluation with 9 polynomials \(P\) gives an approximation of \(\tilde F(z)\) with 15 decimal digits at \(\Re(z)\!>\!4\). |
| − | For small values of |
+ | For small values of \(z\), the iterations of formula \(F(z)=\ln(F(z\!+\!1))\!~ \mathrm e\) |
can be used. |
can be used. |
||
The tetration can be approximated as |
The tetration can be approximated as |
||
| − | : |
+ | : \(\mathrm{tet}_{\exp(1/\mathrm{e})}(z)= F(x_0\!+\!z)\) |
| − | where |
+ | where \(x_0\) is solution of equation \(F(x_0)=1\). |
With the [[complex double]] precision, the resulting approximation returns of order of 14 correct decimal digits in the whole complex plane |
With the [[complex double]] precision, the resulting approximation returns of order of 14 correct decimal digits in the whole complex plane |
||
(except the singularities). |
(except the singularities). |
||
| − | The tetration is aperiodic, holomorphic in the range |
+ | The tetration is aperiodic, holomorphic in the range \(\mathbb C \backslash \{ x\in \mathbb R : x\!\le\! -2 \}\). |
| − | A large values of the argument, it approaches the limiting value |
+ | A large values of the argument, it approaches the limiting value \(\mathrm e\), independently on the direction. |
| − | In particular, along the real axis, the the function shows the monotonic growth from |
+ | In particular, along the real axis, the the function shows the monotonic growth from \(-\infty\) at \(-2\) to \(\mathrm e\) at infinity, passing through points (-1,0) and (0,1). |
| − | At any |
+ | At any \(z\) from the range of definition, In vicinity of \(b\!\approx\!\exp(1/\mathrm e)\), tetration \(\mathrm{tet}_b(z)\) seems to be continuous function of \(b\), although very different agorithms are used for the evaluation in the three cases, |
| − | + | \(1\!<\!b\!<\!\exp(1/\mathrm e)\), |
|
| − | + | \(b=\exp(1/\mathrm e)\), and |
|
| − | + | \(b\!>\!\exp(1/\mathrm e)\). The figure below collects the [[complex map]]s of tetration to base |
|
| − | + | \(b\!=\!1.5\) , left, |
|
| − | + | \(b\!=\!\exp(1/\mathrm e)\) , center, and |
|
| − | + | \(b\!=\!\sqrt{2}\) , right. \(f\!=\! \mathrm{tet}_b(x\!+\!\mathrm i y)\) is shown in the \(x,y\) plane with levels |
|
| − | + | \(~p\!=\!\Re(f)\!=\! \mathrm{const}~\) and levels |
|
| − | + | \(~q\!=\!\Im(f)\!=\! \mathrm{const}~\). The integer values correspond to the thick lines. |
|
| − | [[File:E1efig09abc1a150.png|1200px|left|thumb|[[Complex map]]s of |
+ | [[File:E1efig09abc1a150.png|1200px|left|thumb|[[Complex map]]s of \(\mathrm{tet}_{b}\) for \(b\!=\! 1.5\), \(\exp(1/\mathrm e)\) , \(\sqrt{2}\); \(p\!+\!\mathrm i q=\mathrm{tet}_b(x\!+\!\mathrm i y)\)]] |
| − | ==Behavior at |
+ | ==Behavior at \(b\!\approx\! \exp(1/{\rm e})\), \(z\!\approx\! 0\)== |
| − | If the |
+ | If the \({\mathrm{tet}}_b(z)\) is holomorphic in some vicinity of \(b\!\approx \! \exp(1/{\rm e})\), \(z\!\approx 0\), then it is expandable into the Taylor series |
| − | : |
+ | :\(\displaystyle |
{\mathrm {tet}}_b(x)=1+\sum_{n=1}^{N-1} \! |
{\mathrm {tet}}_b(x)=1+\sum_{n=1}^{N-1} \! |
||
\left(\sum_{m=0}^{M-1} \! |
\left(\sum_{m=0}^{M-1} \! |
||
| Line 125: | Line 128: | ||
\right) x^n |
\right) x^n |
||
+{\mathcal O}(x^N) |
+{\mathcal O}(x^N) |
||
| + | \) |
||
| − | $ |
||
where |
where |
||
| − | + | \(\beta = b\!-\! \exp(1/\mathrm e)\); the coefficients \(c\) of this expansion can be estimated fitting the evaluations of tetration, using the algorithms reported for real base. This leads to the following preliminary estimates: |
|
| − | : |
+ | :\( |
\begin{array}{ccrrrrrr} |
\begin{array}{ccrrrrrr} |
||
m&c_{m,0} &c_{m,1} ~ ~ ~& c_{m,2} ~ ~ ~ & c_{m,3} ~ ~ ~ &c_{m,4}~ ~ ~ \\ |
m&c_{m,0} &c_{m,1} ~ ~ ~& c_{m,2} ~ ~ ~ & c_{m,3} ~ ~ ~ &c_{m,4}~ ~ ~ \\ |
||
| Line 138: | Line 141: | ||
5 & 0 & 1.19090 &-2.12653 &-0.06895& 1.57684 |
5 & 0 & 1.19090 &-2.12653 &-0.06895& 1.57684 |
||
\end{array} |
\end{array} |
||
| + | \) |
||
| − | $ |
||
However, the precision of such evaluation is not so high (perhaps, only two or three decimal digits are significant in the estimates above); for the efficient evaluation of the coefficients of such an expansion, the tetration to the complex base should be analyzed. Such an analysis could be matter for the further research. Any independent confirmation (or correction) of the approximations of the coefficients above should be appreciated. |
However, the precision of such evaluation is not so high (perhaps, only two or three decimal digits are significant in the estimates above); for the efficient evaluation of the coefficients of such an expansion, the tetration to the complex base should be analyzed. Such an analysis could be matter for the further research. Any independent confirmation (or correction) of the approximations of the coefficients above should be appreciated. |
||
| − | ==Behavior at |
+ | ==Behavior at \(b\!>\!\exp(1/\mathrm e)\!\approx 1.44\)== |
| − | Tetration is holomorphic in the whole complex plane except part of the real axis |
+ | Tetration is holomorphic in the whole complex plane except part of the real axis \(\{ x\in \mathbb R : x\le -2 \}\). |
| − | As the real part of the argument goes to |
+ | As the real part of the argument goes to \(-\infty\), the tetration exponentially approaches the fixed point \(L\) at the upper halfplane and \(L^*\) at the lower halfplane, although has [[countable set]] of weak singularities along the cut line \(\{ x\in \mathbb R : x\le -2 \}\). |
As the real part of the argument grows, the tetration shows complicated, [[fractal]]-like structures. In the [[complex map]], the lines of zero real part are reproduced at the unity translations along the real axis, but the new and new details appear at each step. |
As the real part of the argument grows, the tetration shows complicated, [[fractal]]-like structures. In the [[complex map]], the lines of zero real part are reproduced at the unity translations along the real axis, but the new and new details appear at each step. |
||
| − | == Case |
+ | == Case \(b\!=\! \mathrm{e}\)== |
<!--\!=\! \mathrm{e} \!\approx\2.71 !--> |
<!--\!=\! \mathrm{e} \!\approx\2.71 !--> |
||
| + | <div class="thumb tright" style="float:right; width:380px"> |
||
| − | |||
| − | [[File:B271t.png|400px |
+ | [[File:B271t.png|400px]] [[Complex map]] of \(\mathrm{tet}\): |
| + | \( u\!+\!\mathrm i v=\mathrm{tet}(x\!+\!\mathrm i y) \) |
||
| − | The case of [[natural tetration]] refers to base $b\!=\!\mathrm e\! \approx\! 2.71~$; this case is considered in years 2010, 2011 |
||
| + | </div> |
||
| + | The case of [[natural tetration]] refers to base \(b\!=\!\mathrm e\! \approx\! 2.71~\); this case is considered in years 2010, 2011 |
||
<ref name="moc2009"> |
<ref name="moc2009"> |
||
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670. |
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670. |
||
| − | </ref><ref name="vladi"> |
+ | </ref><ref name="vladi"/>. The fast complex(double) implementation in [[C++]] is suggested. |
| − | http://tori.ils.uec.ac.jp/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45. |
||
| − | </ref>. The fast complex(double) implementation in [[C++]] is suggested. |
||
As in the case of exponential, in the indication of the natural tetration, the subscript can be omitted: |
As in the case of exponential, in the indication of the natural tetration, the subscript can be omitted: |
||
| − | + | \(\exp_{\mathrm{e}}=\exp\) and |
|
| − | + | \(\mathrm{tet}_{\mathrm{e}}=\mathrm{tet}\). |
|
The figure shows the [[complex map]] of natural tetration; the real and the imaginary parts of |
The figure shows the [[complex map]] of natural tetration; the real and the imaginary parts of |
||
| − | + | \(f\!=\!\mathrm {tet}(x+\mathrm i y)\) are shown in the \(x\),\(y\) plane with levels |
|
| − | + | \(u\!=\! \Re(f)\!=\! \mathrm {const}\) and |
|
| − | + | \(v\!=\! \Im(f)\!=\! \mathrm {const}\). |
|
| − | In the upper half-plane, the tetration approaches the limiting value, which is [[fixed point]] |
+ | In the upper half-plane, the tetration approaches the limiting value, which is [[fixed point]] \(L\) of natural [[logarithm]]; \(L\) is solution of \(L\!=\!\ln(L)\), and \(L\!\approx\! 0.318132 + 1.33724 \mathrm i\). |
| − | In the lower half-plane, the tetration approaches the conjugated value, id est, |
+ | In the lower half-plane, the tetration approaches the conjugated value, id est, \(L^*\!\approx\! 0.318132 - 1.33724 \mathrm i\). |
==Tetration to complex base== |
==Tetration to complex base== |
||
| + | <div class="thumb tright" style="float:right; width:640px"> |
||
| − | [[File:Tetsheldonmap03.png|660px|thumb| $f=\mathrm{tet}_s(x\!+\!\mathrm i y)$ with |
||
| + | [[File:Tetsheldonmap03.png|660px]] |
||
| − | lines $u\!=\!\Re(f)\!=\!\mathrm{const}$ |
||
| − | + | \(f=\mathrm{tet}_s(x\!+\!\mathrm i y)\) with |
|
| + | lines \(u\!=\!\Re(f)\!=\!\mathrm{const}\) and |
||
| + | lines \(v\!=\!\Im(f)\!=\!\mathrm{const}\) |
||
| + | </div> |
||
| + | |||
The method with the Cauchi equation |
The method with the Cauchi equation |
||
| − | <ref name="moc1"> |
+ | <ref name="moc1"/> |
| − | http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html D.Kouznetsov. (2009). Solutions of $F(z\!+\!1)=\exp(F(z))$ in the complex plane.. Mathematics of Computation, 78: 1647-1670. DOI:10.1090/S0025-5718-09-02188-7. </ref> |
||
can be used also for the complex values of the base. |
can be used also for the complex values of the base. |
||
The following properties should be assumed: |
The following properties should be assumed: |
||
| − | : |
+ | : \(\displaystyle \lim_{y\rightarrow +\infty}\) \(\mathrm{tet}_b(x+\mathrm i y)= \mathrm{Filog}(a)\) |
| − | : |
+ | : \(\displaystyle \lim_{y\rightarrow -\infty}\) \(\mathrm{tet}_b(x+\mathrm i y)= \mathrm{Filog}(a^*)^*\) |
| − | where |
+ | where \(a=\ln(b)\) and [[Filog]] is holomorphic function, \(t=\mathrm{filog}(a)\) is solution of equation |
| − | : |
+ | :\( \log_b(f)=f\) |
The [[Filog]] function can be expressed through the [[Tania function]] and through the [[WrightOmega]] function as follows: |
The [[Filog]] function can be expressed through the [[Tania function]] and through the [[WrightOmega]] function as follows: |
||
| − | : |
+ | : \(\displaystyle \mathrm{Filog}(z)= \frac{\mathrm{Tania}\!\big(\ln(z)-1-\mathrm{i}\big)}{-z} = \frac{\mathrm{WrightOmega}\!\big(\ln(z)-\mathrm{i}\big)}{-z}\) |
===Sheldon base=== |
===Sheldon base=== |
||
The [[complex map]] of |
The [[complex map]] of |
||
| − | + | \(\mathrm{tet}_s\) is shown at figure at right, where \(s\) is the [[Sheldon base]], |
|
| − | : |
+ | : \(\!\!\!\!\!\!\!\! \!\!\!\!\!\!\!\! s=1.52598338517 + 0.0178411853321~{i}\) . |
See the special article [[Tetration to Sheldon base]] for this case. |
See the special article [[Tetration to Sheldon base]] for this case. |
||
| Line 203: | Line 209: | ||
==Fast growth== |
==Fast growth== |
||
| − | Along the real axis, the tetration to base |
+ | Along the real axis, the tetration to base \(b>\exp(1/\mathrm e)\) shows fast growth; it grows faster than any exponential. Due to such a growth, the tetration could be useful for the [[numerical representation of huge numbers]], that can be stored as \(\mathrm {tet}_b(x)\) with moderated values \(x\), keeping the stored value of the number distinguishable from \(+\infty\). The arithmetics for such "tetrational" variables should be implemented using the properties of the tetration, avoiding the conversion to the conventional floating-point form. |
| − | Perhaps, at least in century 21, the tetration satisfies the requirements of the [[computational mathematics]] in the rapidly growing functions; if not, the superfunction of tetration, id est, [[pentation]] ( |
+ | Perhaps, at least in century 21, the tetration satisfies the requirements of the [[computational mathematics]] in the rapidly growing functions; if not, the superfunction of tetration, id est, [[pentation]] (\(\mathrm {pen}_b\)) or even higher [[Ackermann function]]s are available. For natural base (\(b\!=\!\mathrm e\!=\!\exp(1) \approx 2.71\)), the [[pentation]] \(\mathrm{pen}_{\mathrm e}\) can be expressed through the [[regular iteration]], allowing the efficient evaluation while the tetration is already implemented <ref name="vladi"/>. |
<!-- |
<!-- |
||
For the case of natural tetration, the complex double implementations in C++ and than in Mathematica are available at Citizendium; the generators of the figures posted include the codes of the routine used. The details of the implementation are described in the [[Vladikavkaz Mathematical Journal]] |
For the case of natural tetration, the complex double implementations in C++ and than in Mathematica are available at Citizendium; the generators of the figures posted include the codes of the routine used. The details of the implementation are described in the [[Vladikavkaz Mathematical Journal]] |
||
| Line 212: | Line 218: | ||
==Arctetration== |
==Arctetration== |
||
[[Arctetration]] (ate) is inverse function of tetration; it is [[Abel function]] of the [[exponential]]. |
[[Arctetration]] (ate) is inverse function of tetration; it is [[Abel function]] of the [[exponential]]. |
||
| − | Afctetration |
+ | Afctetration \(\mathrm {ate}_b\) to base \(b\) satisfies the relations |
| − | : |
+ | : \(\mathrm{ate}_b(\mathrm{tet}_b(z))=z\) |
| − | : |
+ | : \(\mathrm{tet}_b(\mathrm{ate}_b(z))=z\) |
| − | at least in some ranges of values of |
+ | at least in some ranges of values of \(z\). Also, the arctetration satisfies the [[Abel equation]] |
| − | : |
+ | : \(\mathrm{ate}_b(b^z)=\mathrm{ate}_b(z) +1\) |
Roughly, the arctetration counts, how many times the logarithm should be taken of a value before the value becomes unity. |
Roughly, the arctetration counts, how many times the logarithm should be taken of a value before the value becomes unity. |
||
| Line 224: | Line 230: | ||
The [[superfunction]] and the [[Abel function]] of the exponential are established; they are tetration "tet" and its inverse function "ate". |
The [[superfunction]] and the [[Abel function]] of the exponential are established; they are tetration "tet" and its inverse function "ate". |
||
Then, the iterated exponential can be expressed as follows: |
Then, the iterated exponential can be expressed as follows: |
||
| − | : |
+ | : \( \exp_b^c(z)=\mathrm{tet}_b(c+ \mathrm{ate}_b(z))\) |
| − | In this expression, the number |
+ | In this expression, the number \(c\) of iterations ahs no need to be [[integer number|integer]]; however, at integer values, |
| − | : |
+ | : \(\exp_b^{-2}(z)=\log_b(\log_b(z))\) |
| − | : |
+ | : \(\exp_b^{-1}(z)=\log_b(z)\) |
| − | : |
+ | : \(\exp_b^{0}(z)= z\) |
| − | : |
+ | : \(\exp_b^{1}(z)=\exp_b(z)\) |
| − | : |
+ | : \(\exp_b^{2}(z)=\exp_b(b^z)\) , |
| − | at least for values of |
+ | at least for values of \(z\) in some range in vicinity of the real axis; the arctetration unavoidably has the cut lines in the complex plane. |
<!--The representation through the tetration and arctetration allows to evaluate not only integer iterates but even the complex iterates of the exponential.!--> |
<!--The representation through the tetration and arctetration allows to evaluate not only integer iterates but even the complex iterates of the exponential.!--> |
||
| Line 238: | Line 244: | ||
<!--http://www.ils.uec.ac.jp/~dima/Relle.pdf!--> |
<!--http://www.ils.uec.ac.jp/~dima/Relle.pdf!--> |
||
http://www.digizeitschriften.de/dms/img/?PPN=GDZPPN002175851 |
http://www.digizeitschriften.de/dms/img/?PPN=GDZPPN002175851 |
||
| − | H.Kneser. Reelle analytische Lösungen der Gleichung |
+ | H.Kneser. Reelle analytische Lösungen der Gleichung \(\varphi(\varphi(x))=e^x\). |
Equationes Mathematicae, Journal fur die reine und angewandte Mathematik {\bf 187} 56–67 (1950)</ref> |
Equationes Mathematicae, Journal fur die reine und angewandte Mathematik {\bf 187} 56–67 (1950)</ref> |
||
| − | also allow to express the non-integer iterate of the exponential, but the functions he had constructed are not real along the real axis. For the applications to the real numbers, at least for base |
+ | also allow to express the non-integer iterate of the exponential, but the functions he had constructed are not real along the real axis. For the applications to the real numbers, at least for base \(b\!>\!1\), the representation of iterated exponential through the tetration and arctetration looks more convenient. |
==Representation of huge numbers== |
==Representation of huge numbers== |
||
| Line 246: | Line 252: | ||
In partucular the number [[googol]] <ref name="googol"> |
In partucular the number [[googol]] <ref name="googol"> |
||
http://mathworld.wolfram.com/Googol.html Googol |
http://mathworld.wolfram.com/Googol.html Googol |
||
| − | </ref> which is |
+ | </ref> which is \(10^{100}\) appears to be \(\exp_{10}^2(2) = 10^{10^2}\), while the number [[googolplex]] |
<ref name="googolplex"> |
<ref name="googolplex"> |
||
http://mathworld.wolfram.com/Googolplex.html Googolplex |
http://mathworld.wolfram.com/Googolplex.html Googolplex |
||
</ref> |
</ref> |
||
| − | appears as |
+ | appears as \(\exp_{10}^3(2)=10^{10^{10^2}}\) |
| + | |||
| + | |||
| + | ==[[Superfunctions]]== |
||
| + | Properties of tertration are described in book [[Superfunctions]] (2014–2018) |
||
| + | <ref> |
||
| + | http://www.ils.uec.ac.jp/~dima/BOOK/443.pdf (a little bit out of date) <br> |
||
| + | http://mizugadro.mydns.jp/BOOK/444.pdf |
||
| + | D.Kouznetov. Superfunctions. 2015-2018. |
||
| + | </ref> |
||
| + | |||
| + | After the appearance of the first version of Book [[Superfunctions]], certain advances are observed about evaluation of [[tetration]] |
||
| + | of complex argument; the new algorithm is suggested, that seems to be mode efficient, than the [[Cauchi integral]] described in the Book. |
||
| + | <ref> |
||
| + | http://journal.kkms.org/index.php/kjm/article/view/428 |
||
| + | William Paulsen. |
||
| + | Finding the natural solution to f(f(x))=exp(x). |
||
| + | Korean J. Math. Vol 24, No 1 (2016) pp.81-106. |
||
| + | </ref><ref> |
||
| + | https://link.springer.com/article/10.1007/s10444-017-9524-1 |
||
| + | William Paulsen, Samuel Cowgill. |
||
| + | Solving F(z + 1) = b F(z) in the complex plane. |
||
| + | Advances in Computational Mathematics, December 2017, Volume 43, Issue 6, pp 1261–1282 |
||
| + | </ref><ref> |
||
| + | https://search.proquest.com/openview/cb7af40083915e275005ffca4bfd4685/1?pq-origsite=gscholar&cbl=18750&diss=y |
||
| + | Cowgill, Samuel. Exploring Tetration in the Complex Plane. |
||
| + | Arkansas State University, ProQuest Dissertations Publishing, 2017. 10263680. |
||
| + | </ref><ref> |
||
| + | https://link.springer.com/article/10.1007/s10444-018-9615-7 |
||
| + | William Paulsen. |
||
| + | Tetration for complex bases. |
||
| + | Advances in Computational Mathematics, 2018.06.02. |
||
| + | </ref> |
||
| + | |||
| + | ==Humor about tetration== |
||
| + | [[File:BlackSheep.png|300px|left|thumb|Your generalisation seems to me not supported. All, that we can deduce from this observation, is, that in this country, there exist at least one sheep; and at least the right-hand side of this sheep is black.]] |
||
| + | |||
| + | [[File:2x2uni100.jpeg|300px]] |
||
| + | |||
==References== |
==References== |
||
<references/> |
<references/> |
||
| Line 263: | Line 307: | ||
http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf <br> |
http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf <br> |
||
http://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Press, 2014. In Russian.<br> |
http://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Press, 2014. In Russian.<br> |
||
| − | http://mizugadro.mydns.jp/BOOK/ |
+ | http://mizugadro.mydns.jp/BOOK/444.pdf Dmitrii Kouznetsov. Superfunctions. 2018<br> |
http://myweb.astate.edu/wpaulsen/tetration2.pdf <br> |
http://myweb.astate.edu/wpaulsen/tetration2.pdf <br> |
||
http://link.springer.com/article/10.1007/s10444-017-9524-1 <br> |
http://link.springer.com/article/10.1007/s10444-017-9524-1 <br> |
||
William Paulsen and Samuel Cowgill. |
William Paulsen and Samuel Cowgill. |
||
| − | Solving |
+ | Solving \(F(z+1)=b^{F (z)}\) in the complex plane. |
Advances in Computational Mathematics, 2017 March 7, p. 1–22 |
Advances in Computational Mathematics, 2017 March 7, p. 1–22 |
||
==Keywords== |
==Keywords== |
||
[[Arctetration]], |
[[Arctetration]], |
||
| − | [[Natural tetration]] (to base |
+ | [[Natural tetration]] (to base \(b\!=\!e\!\approx \! 2.71\)), |
[[Pentation]], |
[[Pentation]], |
||
[[Superfunction]], |
[[Superfunction]], |
||
| + | [[Superfunctions]], |
||
[[Tetration to Sheldon base]], |
[[Tetration to Sheldon base]], |
||
| − | [[Transfer equation]] |
+ | [[Transfer equation]], |
| + | [[WrightOmega]] |
||
| + | |||
[[Суперфункции]] |
[[Суперфункции]] |
||
[[Category:Book]] |
[[Category:Book]] |
||
| + | [[Category:English]] |
||
[[Category:Mathematical functions]] |
[[Category:Mathematical functions]] |
||
[[Category:Mathematics]] |
[[Category:Mathematics]] |
||
| + | [[Category:Pentation]] |
||
[[Category:Science]] |
[[Category:Science]] |
||
[[Category:Tetration]] |
[[Category:Tetration]] |
||
| − | [[Category: |
+ | [[Category:Superfunction]] |
[[Category:Superfunctions]] |
[[Category:Superfunctions]] |
||
| − | [[Category:English]] |
||
| − | |||
| − | [[Category:Problem with fig]] |
||
Revision as of 13:12, 5 August 2020
Tetration (or Tetrational) \({\rm tet}_b\) to base \(b \in \mathbb R\), \(b\!>1\)
is the \(\mathbb C \mapsto \mathbb C\) function, which is solution of equations
- \({\rm tet}_b(z\!+\!1) = \exp_b\!\big( {\rm tet}_b(z) \big)\)
- \({\rm tet}_b(0) = 1\)
such that, at least for \(b\!>\!1\), is holomorphic at least in \(\{ z \in \mathbb C : \Re(z)\!>\!-2\}\).
Parameter \(b\) is called "base", as in the cases of exponential and logarithm. According to the first of equations above, \(\mathrm{tet}_b\) is superfunction of exponential to base \(b\). Exponential is transfer function of tetration.
For real \(b\), it is assumed that \({\rm tet}_b(z^*)={\rm tet}_b(z)^*\), where the asterisk means the complex conjugation. For the case of base \(b \!=\! \mathrm e\), the index may be omitted (as in the case of exp and logarithm), id est, \({\rm tet}(z)={\rm tet}_{\rm e}(z)\). The solution is believed to exist and to be unique, although the question about holomorphism with respect to base \(b\) needs to be analyzed.
Case of complex values of \(b\) is under investigation; conditions, that make the solution of equations above unique, may have need to be reformulated.
Contents
- 1 Tetration as superfunction
- 2 Behavior at \(1\!<\!b\!<\exp(1/{\rm e})\)
- 3 Evaluation and behavior at \(b\!=\! \exp(1/{\rm e})\)
- 4 Behavior at \(b\!\approx\! \exp(1/{\rm e})\), \(z\!\approx\! 0\)
- 5 Behavior at \(b\!>\!\exp(1/\mathrm e)\!\approx 1.44\)
- 6 Case \(b\!=\! \mathrm{e}\)
- 7 Tetration to complex base
- 8 Fast growth
- 9 Arctetration
- 10 Iterated exponential
- 11 Representation of huge numbers
- 12 Superfunctions
- 13 Humor about tetration
- 14 References
- 15 Keywords
Tetration as superfunction
Tetration is superfunction of exponential. Tetration can be interpreted as iterated exponential applied to unity. In the language Mathematica, there already exists the special notation for the superfunction, id est, the function Nest. In particular, \({\rm tet}(z)={\rm Nest}[\exp,1,z]\) . Up to year 2011, Nest is implemented only for the integer values of the last argument; the use with any expression, different from an integer constant, causes the error message.
For the beginning of year 2011, the tetration has been analyzed mainly for the real values of base \(b \! > \! 1\). The different algorithms are used for the evaluation at
\(1 \! < \! b \! < \! \exp(1/\rm e)\) [1],
\(b \! = \! \exp(1/\rm e)\approx 1.44\) [2],
and for \(b \! >\! \exp(1/\rm e)\) [3][4][5].
Therefore, one could expect some peculiarity of \({\rm tet}_b(z)\) at \(b\!=\!\exp(1/\rm e)\).
On the other hand, the plots of this function look smooth; one might expect that at a fixed value of \(z\), \({\rm tet}_b(z)\) is holomorphic (analytic) with respect to \(b\), and, in particular, in vicinity of \(b \! \approx \! \exp(1/\rm e)\). However, the visual smoothness at the real values of \(b\) can substitute neither the investigation of the analytic properties for complex \(b\) nor the mathematical proof of holomorphizm.
Behavior at \(1\!<\!b\!<\exp(1/{\rm e})\)
At \(1\!<\!b\!<\exp(1/{\rm e})\), tetration is superfunction constructed with regular iteration at smallest of the real fixed points \(L\!=\!L_1\), \(L\!=\!L_2\) of \(\log_b\). In language Mathematica, the value of the fixed point can be expressed with function ProductLog,
- \(L_1(b)=-(\mathrm{ProductLog}[- \mathrm{Log}[b]]/\mathrm{Log}[b])\).
The tetration is periodic function; the period
- \(T=\frac{2\pi \mathrm i} {\ln(L \, \ln(b))} \)
is pure imaginary. The cut line \(\{x \in \mathbb R: x\le -2\}\) is reproduced at the translations along the imaginary axis.
\(\mathrm{tet}_b(x)\) remains real at \(x>-2\). It has logarithmic singularity at \(x=-2\), and it is [[monotonous function}monotonous]]ly grows at \(x>-2\).
The tetration approaches its fixed point \(L_1=L_1(b)\) at large values of the real part of its argument (and, in particular, along the real axis).
Evaluation and behavior at \(b\!=\! \exp(1/{\rm e})\)
For base \(b\!=\!\exp(1/{\rm e})\! \approx\! 1.44\), the standard regular iteration should be modified.
In partucular, the "new expansion" [2] is suggested:
- \(\displaystyle F(z)=\mathrm e\cdot\left(1-\frac{2}{z}\left( 1+\sum_{m=1}^{M} \frac{P_{m}\big(-\ln(\pm z) \big)}{(3z)^m} +\mathcal{O}\!\left(\frac{|\ln(z)|^{M+1}}{z^{M+1}}\right) \right) \right) \)
where
- \(\displaystyle P_{m}(t)=\sum_{n=0}^{m} ~c_{n,m~}~ t^n\)
The substitution of into equation \(~ F(z\!+\!1)\!=\!\exp(F(z)/\mathrm e)~\) and the asymptotic analysis with small parameter \(|1/z|\) determines the coefficients \(c\) in the polynomials above. In particular,
- \( \begin{array}{ccc} P_{1}(t)&=&t \\ P_{2}(t)&=&t^{2}+t+1/2 \\ P_{3}(t)&=&t^{3}+\frac{ 5}{ 2}t^{2}+\frac{ 5}{2}t +\frac{ 7}{10} \\ P_{4}(t)&=&t^{4}+\frac{13}{ 3}t^{3}+\frac{ 45}{6}t^{2}+\frac{53}{10}t +\frac{ 67}{60} \\ P_{5}(t)&=&t^{5}+\frac{77}{12}t^{4}+\frac{101}{6}t^{3}+\frac{83}{ 4}t^{2}+\frac{653}{60}t+\frac{2701}{1680} \end{array} \)
The evaluation with 9 polynomials \(P\) gives an approximation of \(\tilde F(z)\) with 15 decimal digits at \(\Re(z)\!>\!4\). For small values of \(z\), the iterations of formula \(F(z)=\ln(F(z\!+\!1))\!~ \mathrm e\) can be used.
The tetration can be approximated as
- \(\mathrm{tet}_{\exp(1/\mathrm{e})}(z)= F(x_0\!+\!z)\)
where \(x_0\) is solution of equation \(F(x_0)=1\). With the complex double precision, the resulting approximation returns of order of 14 correct decimal digits in the whole complex plane (except the singularities).
The tetration is aperiodic, holomorphic in the range \(\mathbb C \backslash \{ x\in \mathbb R : x\!\le\! -2 \}\). A large values of the argument, it approaches the limiting value \(\mathrm e\), independently on the direction. In particular, along the real axis, the the function shows the monotonic growth from \(-\infty\) at \(-2\) to \(\mathrm e\) at infinity, passing through points (-1,0) and (0,1).
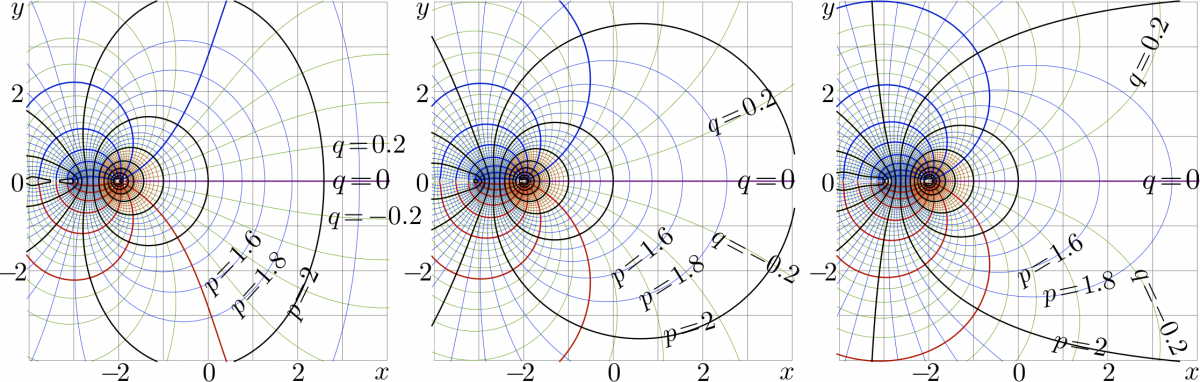
At any \(z\) from the range of definition, In vicinity of \(b\!\approx\!\exp(1/\mathrm e)\), tetration \(\mathrm{tet}_b(z)\) seems to be continuous function of \(b\), although very different agorithms are used for the evaluation in the three cases, \(1\!<\!b\!<\!\exp(1/\mathrm e)\), \(b=\exp(1/\mathrm e)\), and \(b\!>\!\exp(1/\mathrm e)\). The figure below collects the complex maps of tetration to base \(b\!=\!1.5\) , left, \(b\!=\!\exp(1/\mathrm e)\) , center, and \(b\!=\!\sqrt{2}\) , right. \(f\!=\! \mathrm{tet}_b(x\!+\!\mathrm i y)\) is shown in the \(x,y\) plane with levels \(~p\!=\!\Re(f)\!=\! \mathrm{const}~\) and levels \(~q\!=\!\Im(f)\!=\! \mathrm{const}~\). The integer values correspond to the thick lines.
Behavior at \(b\!\approx\! \exp(1/{\rm e})\), \(z\!\approx\! 0\)
If the \({\mathrm{tet}}_b(z)\) is holomorphic in some vicinity of \(b\!\approx \! \exp(1/{\rm e})\), \(z\!\approx 0\), then it is expandable into the Taylor series
- \(\displaystyle {\mathrm {tet}}_b(x)=1+\sum_{n=1}^{N-1} \! \left(\sum_{m=0}^{M-1} \! c_{m,n} \beta^m + O(\beta^M) \right) x^n +{\mathcal O}(x^N) \)
where \(\beta = b\!-\! \exp(1/\mathrm e)\); the coefficients \(c\) of this expansion can be estimated fitting the evaluations of tetration, using the algorithms reported for real base. This leads to the following preliminary estimates:
- \( \begin{array}{ccrrrrrr} m&c_{m,0} &c_{m,1} ~ ~ ~& c_{m,2} ~ ~ ~ & c_{m,3} ~ ~ ~ &c_{m,4}~ ~ ~ \\ 0 & 1 & 0.61061 &-0.23171 & 0.09225 &-0.03757\\ 1 & 0 & 0.69521 & 0.41315 &-0.16027& 0.07007 \\ 2 & 0 &-0.57851 & 0.18323 & 0.49162&-0.15216 \\ 3 & 0 & 0.64730 &-0.62933 &-0.51128& 0.51372\\ 4 & 0 &-0.84098 & 1.23261 & 0.42470&-0.97551 \\ 5 & 0 & 1.19090 &-2.12653 &-0.06895& 1.57684 \end{array} \)
However, the precision of such evaluation is not so high (perhaps, only two or three decimal digits are significant in the estimates above); for the efficient evaluation of the coefficients of such an expansion, the tetration to the complex base should be analyzed. Such an analysis could be matter for the further research. Any independent confirmation (or correction) of the approximations of the coefficients above should be appreciated.
Behavior at \(b\!>\!\exp(1/\mathrm e)\!\approx 1.44\)
Tetration is holomorphic in the whole complex plane except part of the real axis \(\{ x\in \mathbb R : x\le -2 \}\). As the real part of the argument goes to \(-\infty\), the tetration exponentially approaches the fixed point \(L\) at the upper halfplane and \(L^*\) at the lower halfplane, although has countable set of weak singularities along the cut line \(\{ x\in \mathbb R : x\le -2 \}\). As the real part of the argument grows, the tetration shows complicated, fractal-like structures. In the complex map, the lines of zero real part are reproduced at the unity translations along the real axis, but the new and new details appear at each step.
Case \(b\!=\! \mathrm{e}\)
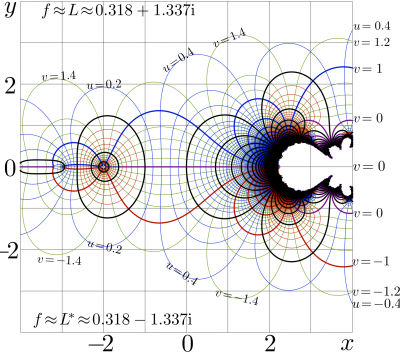 Complex map of \(\mathrm{tet}\):
\( u\!+\!\mathrm i v=\mathrm{tet}(x\!+\!\mathrm i y) \)
Complex map of \(\mathrm{tet}\):
\( u\!+\!\mathrm i v=\mathrm{tet}(x\!+\!\mathrm i y) \)
The case of natural tetration refers to base \(b\!=\!\mathrm e\! \approx\! 2.71~\); this case is considered in years 2010, 2011 [6][4]. The fast complex(double) implementation in C++ is suggested.
As in the case of exponential, in the indication of the natural tetration, the subscript can be omitted: \(\exp_{\mathrm{e}}=\exp\) and \(\mathrm{tet}_{\mathrm{e}}=\mathrm{tet}\).
The figure shows the complex map of natural tetration; the real and the imaginary parts of \(f\!=\!\mathrm {tet}(x+\mathrm i y)\) are shown in the \(x\),\(y\) plane with levels \(u\!=\! \Re(f)\!=\! \mathrm {const}\) and \(v\!=\! \Im(f)\!=\! \mathrm {const}\).
In the upper half-plane, the tetration approaches the limiting value, which is fixed point \(L\) of natural logarithm; \(L\) is solution of \(L\!=\!\ln(L)\), and \(L\!\approx\! 0.318132 + 1.33724 \mathrm i\).
In the lower half-plane, the tetration approaches the conjugated value, id est, \(L^*\!\approx\! 0.318132 - 1.33724 \mathrm i\).
Tetration to complex base
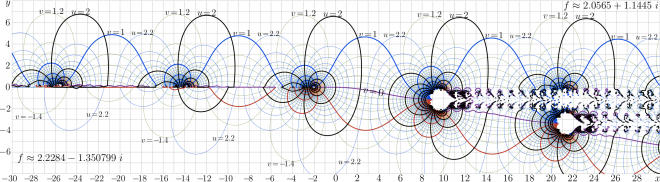 \(f=\mathrm{tet}_s(x\!+\!\mathrm i y)\) with
lines \(u\!=\!\Re(f)\!=\!\mathrm{const}\) and
lines \(v\!=\!\Im(f)\!=\!\mathrm{const}\)
\(f=\mathrm{tet}_s(x\!+\!\mathrm i y)\) with
lines \(u\!=\!\Re(f)\!=\!\mathrm{const}\) and
lines \(v\!=\!\Im(f)\!=\!\mathrm{const}\)
The method with the Cauchi equation [3] can be used also for the complex values of the base. The following properties should be assumed:
- \(\displaystyle \lim_{y\rightarrow +\infty}\) \(\mathrm{tet}_b(x+\mathrm i y)= \mathrm{Filog}(a)\)
- \(\displaystyle \lim_{y\rightarrow -\infty}\) \(\mathrm{tet}_b(x+\mathrm i y)= \mathrm{Filog}(a^*)^*\)
where \(a=\ln(b)\) and Filog is holomorphic function, \(t=\mathrm{filog}(a)\) is solution of equation
- \( \log_b(f)=f\)
The Filog function can be expressed through the Tania function and through the WrightOmega function as follows:
- \(\displaystyle \mathrm{Filog}(z)= \frac{\mathrm{Tania}\!\big(\ln(z)-1-\mathrm{i}\big)}{-z} = \frac{\mathrm{WrightOmega}\!\big(\ln(z)-\mathrm{i}\big)}{-z}\)
Sheldon base
The complex map of \(\mathrm{tet}_s\) is shown at figure at right, where \(s\) is the Sheldon base,
- \(\!\!\!\!\!\!\!\! \!\!\!\!\!\!\!\! s=1.52598338517 + 0.0178411853321~{i}\) .
See the special article Tetration to Sheldon base for this case.
The colored plots of various superexponentials for various complex values of base are available at the Tetration Fortum by Sheldon Levenson [7]; the question wether some of them are tetrations is in discussion.
Fast growth
Along the real axis, the tetration to base \(b>\exp(1/\mathrm e)\) shows fast growth; it grows faster than any exponential. Due to such a growth, the tetration could be useful for the numerical representation of huge numbers, that can be stored as \(\mathrm {tet}_b(x)\) with moderated values \(x\), keeping the stored value of the number distinguishable from \(+\infty\). The arithmetics for such "tetrational" variables should be implemented using the properties of the tetration, avoiding the conversion to the conventional floating-point form.
Perhaps, at least in century 21, the tetration satisfies the requirements of the computational mathematics in the rapidly growing functions; if not, the superfunction of tetration, id est, pentation (\(\mathrm {pen}_b\)) or even higher Ackermann functions are available. For natural base (\(b\!=\!\mathrm e\!=\!\exp(1) \approx 2.71\)), the pentation \(\mathrm{pen}_{\mathrm e}\) can be expressed through the regular iteration, allowing the efficient evaluation while the tetration is already implemented [4].
Arctetration
Arctetration (ate) is inverse function of tetration; it is Abel function of the exponential. Afctetration \(\mathrm {ate}_b\) to base \(b\) satisfies the relations
- \(\mathrm{ate}_b(\mathrm{tet}_b(z))=z\)
- \(\mathrm{tet}_b(\mathrm{ate}_b(z))=z\)
at least in some ranges of values of \(z\). Also, the arctetration satisfies the Abel equation
- \(\mathrm{ate}_b(b^z)=\mathrm{ate}_b(z) +1\)
Roughly, the arctetration counts, how many times the logarithm should be taken of a value before the value becomes unity.
While the tetration is superfunction of the exponential, the arctetration is the Abel function.
Iterated exponential
The superfunction and the Abel function of the exponential are established; they are tetration "tet" and its inverse function "ate". Then, the iterated exponential can be expressed as follows:
- \( \exp_b^c(z)=\mathrm{tet}_b(c+ \mathrm{ate}_b(z))\)
In this expression, the number \(c\) of iterations ahs no need to be integer; however, at integer values,
- \(\exp_b^{-2}(z)=\log_b(\log_b(z))\)
- \(\exp_b^{-1}(z)=\log_b(z)\)
- \(\exp_b^{0}(z)= z\)
- \(\exp_b^{1}(z)=\exp_b(z)\)
- \(\exp_b^{2}(z)=\exp_b(b^z)\) ,
at least for values of \(z\) in some range in vicinity of the real axis; the arctetration unavoidably has the cut lines in the complex plane.
The realizations of the super-exponentials and the Abel–exponential by Hellmuth Kneser [8] also allow to express the non-integer iterate of the exponential, but the functions he had constructed are not real along the real axis. For the applications to the real numbers, at least for base \(b\!>\!1\), the representation of iterated exponential through the tetration and arctetration looks more convenient.
Representation of huge numbers
The tetration and the iterated exponential can be used for the representation of huge numbers. In partucular the number googol [9] which is \(10^{100}\) appears to be \(\exp_{10}^2(2) = 10^{10^2}\), while the number googolplex [10] appears as \(\exp_{10}^3(2)=10^{10^{10^2}}\)
Superfunctions
Properties of tertration are described in book Superfunctions (2014–2018) [11]
After the appearance of the first version of Book Superfunctions, certain advances are observed about evaluation of tetration of complex argument; the new algorithm is suggested, that seems to be mode efficient, than the Cauchi integral described in the Book. [12][13][14][15]
Humor about tetration
References
- ↑
http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf
http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756. - ↑ 2.0 2.1
http://www.ams.org/journals/mcom/0000-000-00/S0025-5718-2012-02590-7/S0025-5718-2012-02590-7.pdf
http://www.ils.uec.ac.jp/~dima/PAPERS/2011e1e.pdf H.Trappmann, D.Kouznetsov. Computation of the Two Regular Super-Exponentials to base exp(1/e). Mathematics of computation, 2012 February 8. ISSN 1088-6842(e) ISSN 0025-5718(p) - ↑ 3.0 3.1 http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html D.Kouznetsov. (2009). Solutions of \(F(z+1)=\exp(F(z))\) in the complex plane.. Mathematics of Computation, 78: 1647-1670. DOI:10.1090/S0025-5718-09-02188-7.
- ↑ 4.0 4.1 4.2 http://www.ils.uec.ac.jp/~dima/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45.
- ↑ http://www.springerlink.com/content/u7327836m2850246/ H.Trappmann, D.Kouznetsov. Uniqueness of Analytic Abel Functions in Absence of a Real Fixed Point. Aequationes Mathematicae, v.81, p.65-76 (2011)
- ↑ http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670.
- ↑ http://math.eretrandre.org/tetrationforum/showthread.php?tid=729 Sheldon Levenson. Complex base tetration program. Tetration and Related Topics, 2012 March 1.
- ↑ http://www.digizeitschriften.de/dms/img/?PPN=GDZPPN002175851 H.Kneser. Reelle analytische Lösungen der Gleichung \(\varphi(\varphi(x))=e^x\). Equationes Mathematicae, Journal fur die reine und angewandte Mathematik {\bf 187} 56–67 (1950)
- ↑ http://mathworld.wolfram.com/Googol.html Googol
- ↑ http://mathworld.wolfram.com/Googolplex.html Googolplex
- ↑
http://www.ils.uec.ac.jp/~dima/BOOK/443.pdf (a little bit out of date)
http://mizugadro.mydns.jp/BOOK/444.pdf D.Kouznetov. Superfunctions. 2015-2018. - ↑ http://journal.kkms.org/index.php/kjm/article/view/428 William Paulsen. Finding the natural solution to f(f(x))=exp(x). Korean J. Math. Vol 24, No 1 (2016) pp.81-106.
- ↑ https://link.springer.com/article/10.1007/s10444-017-9524-1 William Paulsen, Samuel Cowgill. Solving F(z + 1) = b F(z) in the complex plane. Advances in Computational Mathematics, December 2017, Volume 43, Issue 6, pp 1261–1282
- ↑ https://search.proquest.com/openview/cb7af40083915e275005ffca4bfd4685/1?pq-origsite=gscholar&cbl=18750&diss=y Cowgill, Samuel. Exploring Tetration in the Complex Plane. Arkansas State University, ProQuest Dissertations Publishing, 2017. 10263680.
- ↑ https://link.springer.com/article/10.1007/s10444-018-9615-7 William Paulsen. Tetration for complex bases. Advances in Computational Mathematics, 2018.06.02.
http://www.proofwiki.org/wiki/Definition:Tetration
http://en.citizendium.org/wiki/Tetrational
http://en.wikipedia.org/wiki/Tetration
http://math.eretrandre.org/tetrationforum/index.php
http://samlib.ru/k/kuznecow_d_j/ackermann.shtml
http://www.tetration.org/Ackermann/arithmetic.html Daniel Geisler. All is Arithmetic. (2009)
https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf
http://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Press, 2014. In Russian.
http://mizugadro.mydns.jp/BOOK/444.pdf Dmitrii Kouznetsov. Superfunctions. 2018
http://myweb.astate.edu/wpaulsen/tetration2.pdf
http://link.springer.com/article/10.1007/s10444-017-9524-1
William Paulsen and Samuel Cowgill.
Solving \(F(z+1)=b^{F (z)}\) in the complex plane.
Advances in Computational Mathematics, 2017 March 7, p. 1–22
Keywords
Arctetration, Natural tetration (to base \(b\!=\!e\!\approx \! 2.71\)), Pentation, Superfunction, Superfunctions, Tetration to Sheldon base, Transfer equation, WrightOmega