Difference between revisions of "Theorem on increment of tetration"
| Line 10: | Line 10: | ||
The matter of the Theorem is coincidence of two curves (thick red and thin black) in Fig.1. |
The matter of the Theorem is coincidence of two curves (thick red and thin black) in Fig.1. |
||
These curves represent imaginary part of the growing factor \(K\) and that of the increment \(k\) of the asymptotic solution versus logarithm of the base. |
These curves represent imaginary part of the growing factor \(K\) and that of the increment \(k\) of the asymptotic solution versus logarithm of the base. |
||
| − | From the first glance, the |
+ | From the first glance, the overlapping of the curves may look strange. |
The Theorem indicates, that it is not an occasional coincidence, but the unavoidable equality. |
The Theorem indicates, that it is not an occasional coincidence, but the unavoidable equality. |
||
Revision as of 14:26, 12 August 2020
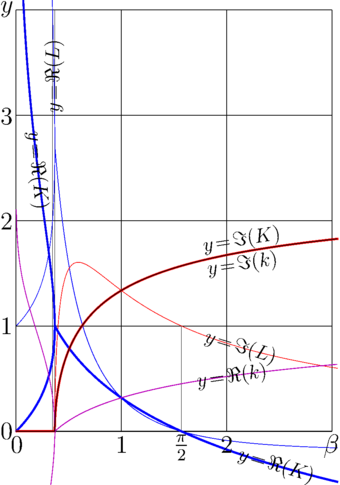 Fig.1. Asymptoric parameters of Tetration versus \(\beta\)
Fig.1. Asymptoric parameters of Tetration versus \(\beta\)
Theorem on increment of tetration is statement about asymptotic behavior of solution of the Transfer equation with exponential transfer functions.
The matter of the Theorem is coincidence of two curves (thick red and thin black) in Fig.1. These curves represent imaginary part of the growing factor \(K\) and that of the increment \(k\) of the asymptotic solution versus logarithm of the base. From the first glance, the overlapping of the curves may look strange. The Theorem indicates, that it is not an occasional coincidence, but the unavoidable equality.
The therorem applies not only to tetration, but also to other superexponentials.
Statement
Let \(F\) be solution of equation
\(F(z\!+\!1)=\exp\big(\beta F(z)\big)\)
for some \(\beta>0\).
Let \(L\) be the fixed point, id est, \(\exp(\beta L)=L\)
Let \(F(z)=L+\varepsilon+O(\varepsilon^2) \)
where \(\varepsilon = \exp(kz) \) for some increment \(k\).
Let \(~ K\!=\!\exp(k)\)
Then
\( \Im(K) = \Im(k) \)
Proof
Substitution of the asymptotic of solutioun \(F\) into the transfer equation gives
\( K=\beta L = \ln(\beta) \)
Then, \( \exp(k)=\beta L\)
\( k=\ln(\beta\, L) =\) \(\ln(L) + \ln(\beta) =\) \(K + \ln(\beta) \)
While \( \beta >0 \), its logarithm is real.
Hence, the imaginary parts of \(k\) and \(K\) are the same.
(End of proof)
The quantities mentioned are plotted in Fig.1 as functions of \(\beta\)
Applications
Fig.1 shows the asymptotic parameters of tetration to base \(\ln(\beta)\):
Real and imaginary parts of the fixed points
\(L=L_1=\) Filog\((\beta)\)
and
\(L=L_2=\) Filog\((\beta^*)^*\)
Real and imaginary parts of the asymptotic growing factor
\(K= \beta L\)
Real and imaginary parts of the asymptotic increment
\(k=\ln(K) \)
For \(\beta < 1/\mathrm e\), the two fixed points are shown; and the two values of the corresponding growing factor and two values of the corresponding increment are drown.
For real positive \(\beta\),
The imaginary parts of \(K\) and \(k\) coincide.
References
http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002175851&physid=phys63#navi Hellmuth Kneser. Reelle analytische Lösungen der Gleichung \(\varphi(\varphi(x)=e^x\) und verwandter Funktionalgleichungen. Journal für die reine und angewandte Mathematik / Zeitschriftenband (1950) / Artikel / 56 - 67
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf D.Kouznetsov. Analytic solution of F(z+1)=exp(F(z)) in complex z-plane. Mathematics of Computation, v.78 (2009), 1647-1670.
http://www.vmj.ru/articles/2010_2_4.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45, Russian version.
http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=vmj&paperid=10&option_lang=eng
D.Yu.Kuznetsov. “Tetrational as special function”, Vladikavkaz. Mat. Zh., 12:2 (2010), 31–45,
English version.
http://link.springer.com/article/10.1007/s10444-017-9524-1 William Paulsen and Samuel Cowgill. Solving F(z+1)=bF(z) in the complex plane. Advances in Computational Mathematics, 2017 March 7, p. 1–22
https://www.morebooks.de/store/gb/book/superfunctions/isbn/978-620-2-67286-3 Dmitrii Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020.
Keywords
Asymptotic analysis, Filog, Fixed point, Growing factor, Increment, Kneser Expansion, Superfunction, Tetration