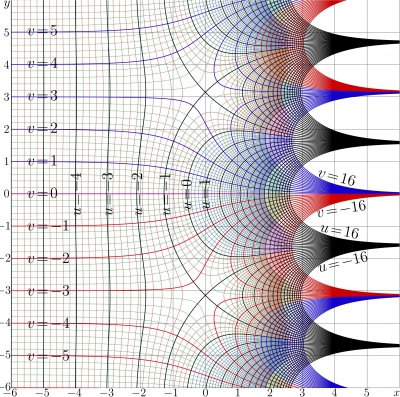
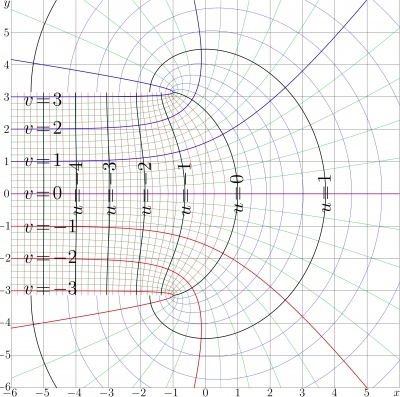
Trappmann function
Trappmann function $~\mathrm{Tra}(z)=\mathrm e^z +z~$ is example of entire function without fixed points, suggested in year 2011 by Henryk Trappmann [1]. The absence of fixed points was considered as a serious obstacle at the building-up its superfunction, the Abel function and the non–integer iterates of function Tra.
According to the general statement by [2], it is possible to construct at least one superfunction for any holomorphic function. Therefore, the consideration of the Trappmann function as transfer function is important.
Contents
About the names
The name of function $\mathrm{Tra}$ or $\mathrm{tra}$ is chosen after the last name of Henryk Trappmann [1], because it begins with letter $T$, often used to denote the Transfer function. The question, wether to capitalize the first letter in the name of the function or not, is still under investigation.
In the similar way, the superfunction of function $\mathrm{Tra}$ may be called Hen or hen using the first name Henryk.
The inverse function, id est, the Abel function of $\mathrm{Tra}$, may be called Ahe or ahe, in a way similar to that used to create names SuZex and AuZex of the superfunction and the Abel function of transfer function zex.
In this article, the properties of functions Tra, hen and ahe are described.
Inverse function
Inverse function, id est, $\mathrm{ArcTra}=\mathrm{Tra}^{-1}$ can be expressed through the WrightOmega function as well as through the Tania function as follows:
$\mathrm{ArcTra}(z)=z-\mathrm{Tania}(z\!-\!1)= z-\mathrm{WrightOmega}(z)$
The complex map of the ArcTra function is shown in Figure 2.
Exponential modification, superfunction and the Abel function
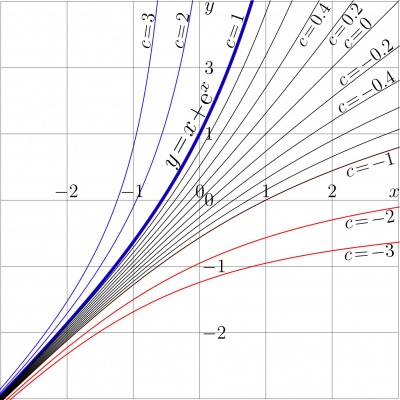
Idea by Henryk is that it the fixed point does not exist, them we should create it, modifying the Transfer function. The simple modification is described in this section. Let the Transfer function $T$ be defined with
(1) $ ~ ~ ~ T(z)=\mathrm{Tra}(z)=\mathrm e^z+z$
Let $~F\!=\!\mathrm{hen}~$ be its superfunction and $~G\!=\!F^{-1}\!=\!\mathrm{ahe}~$ be its superfunction and the Abel function. The superfunction should satisfy the transfer equation
(2) $~ ~ ~ T\!\Big(F(x)\Big) = F(z\!+\!1)$
and the Abel function should satisfy the Abel equation
(3) $~ ~ ~ G\!\Big(T(x)\Big) = G(z) + 1$
Search the solution for $F$ in the following form:
(4) $ ~ ~ ~ F(z)=\ln\!\Big(h(z)\Big)$
where $h$ is some holomorphic function. The reason for this representation is a hope, that the corresponding transfer equation for $h$ will be simpler, than the initial transfer equation Form (4), function $h$ can be expressed as follows:
(5) $~ ~ ~ h(z)=\exp\!\Big(F(z)\Big)$
Substituting representation (2) into the transfer equation (2) gives
(6) $ ~ ~ ~ T\!\Big(\ln\big(h(z)\big)\Big)=\ln\!\Big(h(z\!+\!1)\Big)$
Using equation (1), equation (6) gives:
(7) $ ~ ~ ~ h(z\!+\!1) = \exp\!\Big( T\!\Big(\ln\big(h(z)\big)\Big) \Big)= \exp\!\Big( h(z) +\ln\big(h(z)\big)\Big) = h(z) \ln\!\Big(h(z)\Big)=\mathrm{zex}\!\Big( h(z) \Big)$
where
(8) $ ~ ~ ~ \mathrm{zex}(z)=x\, \exp(z)$
Properties of function zex are already described, and SuZex is its superfunction, id est, $h=\mathrm{Suzex}$ is solution of equation
(9) $ ~ ~ ~ h(z\!+\!1) = \mathrm{zex}\!\Big( h(z) \Big)$
Therefore, solution of the transfer equation (2) for $T=\mathrm{Tra}$ is
(10) $ ~ ~ ~ F(z) =\mathrm{hen}(z) = \ln\!\Big(\mathrm{SuZex}(z) \Big)$
and the corresponding Abel function $G$ can be expressed with
(11) $ ~ ~ ~ G(z) =\mathrm{ahe}(z)= \mathrm{AuZex}\!\Big( \exp(z) \Big)$
The efficient algorithms for evaluation of SuZex and AuZex are already loaded; so, the evaluation of the superfunction hen and the Abel function ahe for transfer function Tra by (1) should not cause any difficulties. With these functions, the non-integer iterates of the Trappmann function are evaluated to plot figure 1.
Inverse function and non-integer iterate
With superfunction $F$ and the Abel function $G$ by (10) and (11), the inverse function of $\mathrm{tra}$ can be expressed also in the following form
(12) $ ~ ~ ~ \mathrm{tra}^{-1}(z)=F\!\Big(-1+G(z)\Big)$
This expression corresponds to the curve with $c\!=\!-1$ in Figure 1. In general, the $c$th iteration can be expressed as usually,
(13) $ ~ ~ ~ \mathrm{tra}^{c}(z)=F\!\Big(c+G(z)\Big)$
The function without fixed point does not break the general concept; it seems, the non-integer iterates can be defined for any holomorphic transfer function.
References
- ↑ 1.0 1.1 http://math.eretrandre.org/publications.html Publication List Henryk Trappmann.
- ↑ http://www.springerlink.com/content/qt31671237421111/fulltext.pdf?page=1 D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12.
Keywords
Henryk Trappmann, Transfer function, Transfer equation, Superfunction, Abel function, Abel equation, Fixed point, Iteration, LambertW, Zex, SuZex, AuZex