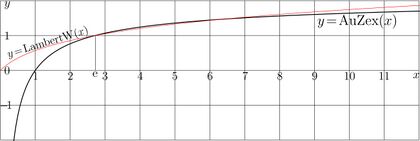
AuZex Approximation
AuZex Approximation describes the approximations of AuZex, which is inverse function of SuZex and Abel function of zex.
The resulting complex double implementation is loaded as AuZex.cin
The explicit plot of function AuZex is shown in figure 1.
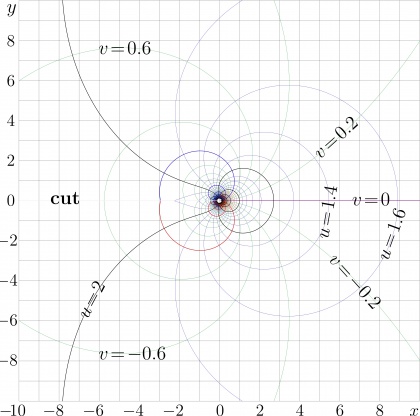
Its complex map is shown in figure 2.
The approximation is described in Chapter 11 of book «Superfunctions», 2020 [1][2].
Background
AuZex is Inverse function of SuZex, so, in wide ranges of values of $z$, the relations
(1) \( ~ ~ ~ \mathrm{SuZex}\Big( \mathrm{AuZex}(z) \Big) = z \)
and
(2) \( ~ ~ ~ \mathrm{AuZex}\Big( \mathrm{SuZex}(z) \Big) = z \)
should hold. In particular, \(~\mathrm{AuZex}(1)=0\ \).
Also, AuZex satisfies the Abel equation
(3) \( ~ ~ ~ \mathrm{AuZex}\Big( \mathrm{zex}(z) \Big) = \mathrm{AuZex}(z) +1\)
in this case, zex appears as transfer function, and AuZex is its Abel function. Iterations of equation (3) gives the relations
(4) \( ~ ~ ~ \mathrm{AuZex}\Big( \mathrm{zex}^n(z) \Big) = \mathrm{AuZex}(z) +n\)
This can be re-writtern also as
(5) \( ~ ~ ~ \mathrm{AuZex}\Big( \mathrm{LambertW}^n(z) \Big) = \mathrm{AuZex}(z) - n\)
as LambertW is inverse function of zex.
The relations above indicate ways to construct the efficient approximation of AuZex, covering the whole complex plane, and make the efficient (fast and precise) implementation.
Taylor expansion at unity
Coefficients in expansion (3)
- \(\!\!\!\!\!\!\!\!\!\! \displaystyle \begin{array}{r|r} n & c_n~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ \\ \hline 0 & 0.0000000000000000 \\ 1 & 1.4011764331478447\\ 2 & -1.2313176379841106\\ 3 & 1.1612567820116564\\ 4 & -1.1231269305776580\\ 5 & 1.0992876544297898\\ 6 & -1.0830479804216504\\ 7 & 1.0713113178859344\\ 8 & -1.0624516150969114 \end{array} \)
Some tens of coefficients of the Taylor expansion of function AuZex can be evaluated just inverting the Taylor expansion of $\mathrm{SuZex}(z)$ at \(z\!=\!0\); that leads to the approximation
(3) \( ~ ~ ~ \displaystyle \mathrm{AuZex}(1+t)\approx\mathrm{AuZt}_N(1\!+\!t)=\sum_{n=1}^N c_n t^n \)
Approximatoins for the first eight coefficients \(c\) are shown in the table at right.
The approximation AuZt with \(N\!=\!32\) with 32 terms is denoted as \(\mathrm{AuZt}_{32}\).
The agreement is estimated as
(4) \( ~ ~ ~ \displaystyle A(z)=-\lg\left( \frac {\left|\mathrm{SuZex}\Big(\mathrm{AuZt}_{32}(z)\Big)- z\right|} {\left|\mathrm{SuZex}\Big(\mathrm{AuZt}_{32}(z)\Big)\right|+|z|} \right) \)
Iterations of function LambertW applied to the argument of function AuZt give the approximation
(5) \( ~ ~ ~ \displaystyle \mathrm{AuZex}(z) \approx \mathrm{AuZt}_n( \mathrm{LambertW}^n(z))+n\)
Asymptotic expansion
The approximations by (5) cover the most of the complex plane, except the region in vicinity of the origin of coordinates. For this region, the asymptotic expansion below van be used:
(6) \( ~ ~ ~ \displaystyle \mathrm{AuZex}(z) \approx \mathrm{AsZa}_N\Big(\mathrm{LambertW}^m(z)\Big)+x_1+m\)
where
(7) \( ~ ~ ~ \displaystyle \mathrm{AsZa}_N(t)=\frac{-1}{t} + \frac{1}{2} \ln(t) + \sum_{n=1}^N ~ b_n\, t^n\)
The coefficients \(b\) of this expansion can be generated by Mathematica with code
So1[z_, a_] := Extract[Extract[Solve[z, a], 1], 1]
zex[z_] = z Exp[z]
Clear[b];
g[n_,z_] = -1/z + Log[z]/2 + Sum[b[m] z^m, {m, 1, n}]
For[k=1,k<64,
b[k]=ReplaceAll[b[k],So1[Coefficient[Series[g[k,zex[z]]-g[k,z]-1,{z,0,k+1}],z^(k+1)]==0, b[k]]];
Print[b[k]]; k++]
Coefficients \(b_n\) for \(n\!=\!1..9\) are shown in the table
\(\begin{array}{c|ccl} n & b_n & &{\rm ~approximation ~ of~ ~} b_n\\ \hline \\ 1 & -1/6 &\approx&-0.1666666666666666667\\ 2 & 1/16 &\approx& ~ ~ ~ 0.0625\\ 3 & -19/540&\approx& -0.0351851851851851852 \\ 4 & 1/48&\approx& ~ ~ ~ 0.0208333333333333333 \\ 5 & -41/4200&\approx& -0.0097619047619047619\\ 6 & 37/103680&\approx& ~ ~ ~ 0.00035686728395061728\\ 7 & 18349/3175200&\approx&~ ~ ~ 0.005778848576467624 \\ 8 & -443/80640 &\approx& -0.005493551587301587\\ 9 & 55721/21555072&\approx& -0.002585052835824441 \end{array} \)
Implementation of AuZex
The approximations above cover the whole complex plane. On the base of these approximations, the complex double function AuZex is implemented. The implementation is available as AuZex.cin. This implementation provides of order of 15 correct decimal digits, and the errors are comparable to the rounding errors at the Complex double arithmetics.
Exotic iteration
Similar approach is used to implement two Abel functions of the exponential to to base \(b=\exp^2(-1)=\exp(1/\mathrm e)\approx 1.444667861\) [3]. In that case, the transfer function \(\exp_b\) also has derivative unity at its fixed point \(L=\mathrm e\approx 2.718\)
The similarity is that the Regular iteration cannot be applied "as is"; the logarithmic terms appear in the expansion.
The described way to evaluate the superfunction, the abelfunction and non-integer iterates of the transfer function in such a case is denoted with term Exotic iteration.
References
- ↑ https://www.amazon.com/Superfunctions-Non-integer-holomorphic-functions-superfunctions/dp/6202672862 Dmitrii Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020. Tools for evaluation of superfunctions, abelfunctions and non-integer iterates of holomorphic functions are collected. For a given transferfunction T, the superfunction is solution F of the transfer equation F(z+1)=T(F(z)) . The abelfunction is inverse of F. In particular, superfunctions of factorial, exp, sin are suggested. The Holomorphic extensions of the logistic sequence and those of the Ackermann functions are considered. Among ackermanns, the tetration (mainly to the base b>1) and natural pentation (to base b=e) are presented. The efficient algorithm for the evaluation of superfunctions and abelfunctions are described. The graphics and complex maps are plotted. The possible applications are discussed. Superfunctions significantly extend the set of functions, that can be used in scientific research and technical design.
- ↑ https://mizugadro.mydns.jp/BOOK/468.pdf Dmitrii Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020.
- ↑ http://tori.ils.uec.ac.jp/PAPERS/2012e1eMcom2590.pdf H.Trappmann, D.Kouznetsov. Computation of the Two Regular Super-Exponentials to base exp(1/e). Mathematics of Computation, 2012 February 8. ISSN 1088-6842(e) ISSN 0025-5718(p)
Keywords
«Abel function», «Abelfunction», «AuZex», «AuZex.cin», «Abel function», «Exotic iteration», «LambertW», «Exotic iteration», «Mathematics of Computation», «Superfunctions», «Zex»,