File:AteSuExq2plotU.png
AteSuExq2plotU.png (737 × 438 pixels, file size: 11 KB, MIME type: image/png)
Summary
Explicit plot of combination of natural ArcTetration and growing SuperExponential to base \(\sqrt{2}\):
\(y=\mathrm{ate}\Big(\mathrm{SuExq2}(x)\Big)\)
Here \(\mathrm{SuExq2}\) is SuperExponential to base \(\sqrt{2}\) constricted as regular iteration at fixed point 4 and placed so that \(\ \mathrm{SuExq2}(0)\!=\!1\ \).
C++
/* ado.cin, SuExq2.cin, fslog.cin should be also loaded */
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include <complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include"ado.cin"
#define M(x,y) fprintf(o,"%6.4f %6.4f M\n",1.*(x),1.*(y));
#define L(x,y) fprintf(o,"%6.4f %6.4f L\n",1.*(x),1.*(y));
//#include "Conrec6.cin"
//#include "fac.cin"
//#include "SuFac.cin"
#include "SuExq2.cin"
#include "fslog.cin"
//#include "filog.cin"
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;
FILE *o;o=fopen("AteSuExq2plot.eps","w");ado(o,708,408);
fprintf(o,"104 4 translate\n 100 100 scale\n");
for(m=-1;m<7;m++){M(m,0)L(m,4)}
for(n=0;n<5;n++){M(-1,n)L(6,n)}
//M(0,.8)L(3,.8) // horisontal line
//M(-0.8,0)L(3+.2,.8+3+.2)
M(2,0)L(6,4)
fprintf(o,"2 setlinecap .008 W 0 0 0 RGB S\n");
for(m=-10;m<57;m++) { x=.1*(m-.6);
//c=superfac(x); //SuFac
c=F45E(x); // if(abs(c)>1.e28) break;
c=FSLOG(c); // ate
y=Re(c); if(m==-10) M(x,y) else L(x,y)
}
fprintf(o,".03 W 1 0 0 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
system("epstopdf AteSuExq2plot.eps");
system( "open AteSuExq2plot.pdf"); //for mac
}
Latex
\documentclass[12pt]{article}
\usepackage[utf8]{inputenc}
\usepackage[T2A]{fontenc}
\usepackage[russian]{babel}
\usepackage{geometry}
\usepackage{latexsym,amsmath,amssymb,amsbsy,graphicx}
%\usepackage{graphicx}
\usepackage{wrapfig}
\usepackage{hyperref}
\usepackage{rotating}
\usepackage[export]{adjustbox}
\paperwidth 740pt
\paperheight 440pt
\topmargin -114pt
\textheight 740pt
\oddsidemargin -66pt
\textwidth 512pt
\newcommand{\ing}{\includegraphics}
\newcommand{\sx}{\scalebox}
\newcommand{\rot}{\begin{rotate}}
\newcommand{\ero}{\end{rotate}}
\parindent 0px
\begin{document}
%\sx{.82}
{\begin{picture}(740,440)
%\put(20,20){\ing{AteSuFacMap}}
\put(20,20){\ing{AteSuExq2plot.pdf}}
\put(3,410){\sx{2.7}{\(y\)}}
\put(3,317){\sx{2.5}{\(3\)}}
\put(3,217){\sx{2.4}{\(2\)}}
\put(3,117){\sx{2.4}{\(1\)}}
\put(3,018){\sx{2.4}{\(0\)}}
\put( 1,0){\sx{2.4}{\(-1\)}}
\put(119,0){\sx{2.4}{\(0\)}}
\put(219,0){\sx{2.4}{\(1\)}}
\put(319,0){\sx{2.4}{\(2\)}}
\put(419,0){\sx{2.4}{\(3\)}}
\put(519,0){\sx{2.4}{\(4\)}}
\put(619,0){\sx{2.4}{\(5\)}}
\put(710,1){\sx{2.6}{\(x\)}}
\put(438,229){\sx{2.2}{\rot{34}\(y\!=\!\mathrm{ate}\Big(\mathrm{SuExq2}(x)\Big)\)\ero}}
\put(556,229){\sx{2.2}{\rot{44}\(y\!=x\!-\!2\)\ero}}
\end{picture}}
\end{document}
Explicit plot of combination of natural ArcTetration and growing SuperExpnential to base \(\sqrt{2}\):
\(y=\mathrm{ate}\Big(\mathrm{SuExq2}(x)\Big)\)
Here
\(\mathrm{SuExq2}\)
The picture cries for the following conjectures:
In vicinity of the real axis, the levels for almost equidistant grid,
as abscissa increases, the derivative approaches unity.
This observation can be formulated as a set of conjectures:
{\bf Conjecture 0}
There exist real constant \(x_0\) and domain \(D\subset\mathbb C\) that includes the poisitive real axis such that
\[
\mathrm {SuExq2}(z) \underset{\mathrm{ate},\ z\to \infty, \ z\in D}{\sim} \mathrm{tet}\big( z\!-\!x_0+\mathcal O(1/z)\big)
\]
Conjecture 1
There exist real constant \(x_0\) and positive decreasing function \(\varepsilon\) such that
\[
\lim_{x\to \infty, |y|<\varepsilon(x)}
\Big(
\mathrm{ate}\big(\mathrm{SuExq2}(x\!+\!\mathrm i y)\big) - \big((x\!+\!\mathrm i y) - x_0 \big)\Big) = 0
\]
Conjecture 2
For \(x>3\),
\[
\mathrm{tet}(x-2)
<
\mathrm{SuExq2}(x)
<
\mathrm{tet}(x-1)
\]
Conjecture 3
The constant \(x_0 \approx 1.93 \)
\vskip 12pt
\sx{1.4}{\bf References}
\vskip 6pt
\url{https://mizugadro.mydns.jp/BOOK/468.tex}
D.Kouznetwov. Superfunctions. Lambert Academic Publishing, 2020
\vskip 5pt
\url{http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html} \\
\url{https://mizugadro.mydns.jp/PAPERS/2010sqrt2.pdf}
D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.
\vskip 5pt
\url{http://www.vmj.ru/articles/2010_2_4.pdf}
D.Kouznetsov. Tetration as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45, In Rusian. English version:
\url{https://mizugadro.mydns.jp/PAPERS/2009vladie.pdf}
\vskip 4pt
\end{document}
Congectures
The picture cries for the following conjectures:
{\bf Conjecture 0}
There exist real constant \(x_0\) and domain \(D\subset\mathbb C\) that includes the poisitive real axis such that \[ \mathrm {SuExq2}(z) \underset{\mathrm{ate},\ z\to \infty, \ z\in D}{\sim} \mathrm{tet}\big( z\!-\!x_0+\mathcal O(1/z)\big) \]
Conjecture 1
There exist real constant \(x_0\) and positive decreasing function \(\varepsilon\) such that \[ \lim_{x\to \infty, |y|<\varepsilon(x)} \Big( \mathrm{ate}\big(\mathrm{SuExq2}(x\!+\!\mathrm i y)\big) - \big((x\!+\!\mathrm i y) - x_0 \big)\Big) = 0 \]
Conjecture 2
For \(x>3\), \[ \mathrm{tet}(x-2) < \mathrm{SuExq2}(x) < \mathrm{tet}(x-1) \]
Conjecture 3
The constant \(x_0 \approx 1.93 \)
References
https://mizugadro.mydns.jp/BOOK/468.tex D.Kouznetwov. Superfunctions. Lambert Academic Publishing, 2020
http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html
https://mizugadro.mydns.jp/PAPERS/2010sqrt2.pdf
D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.
http://www.vmj.ru/articles/2010_2_4.pdf D.Kouznetsov. Tetration as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45, In Rusian. English version: https://mizugadro.mydns.jp/PAPERS/2009vladie.pdf
Kaywords
Keywords
«ArcTetration», «Asymptotic», «Asymptotics», «Base sqrt2», «Exponential», «Natural tetration», «SuperExponential», «Superfunction», «Superfunctions», «Tetration»,
«ado.cin», «SuExq2.cin», «fslog.cin»
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 21:32, 28 January 2026 | 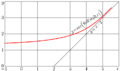 | 737 × 438 (11 KB) | T (talk | contribs) | == Summary == {{oq|AteSuExq2plotU.png|AteSuExq2plotU.png (737 × 438 pixels, file size: 11 KB, MIME type: image/png)}} Explicit plot of combination of natural ArcTetration and growing SuperExponential to base \(\sqrt{2}\): \(y=\mathrm{ate}\Big(\mathrm{SuExq2}(x)\Big)\) Here \(\mathrm{SuExq2}\) is SuperExponential to base \(\sqrt{2}\) constricted as regular iteration at fixed point 4 and placed so that \(\ \mathrm{SuExq2}(0)\!=\!1\ \). == C++ == /* ado.cin, <!--[[Con... |
You cannot overwrite this file.
File usage
There are no pages that use this file.
