Difference between revisions of "File:Hermiten.jpg"

From TORI
Jump to navigation Jump to search
(Importing image file)
 
 
Line 1: Line 1:
  +
Normalized
−
Importing image file
  
  +
[[Hermite polynomial]]s,
  +
  +
$y=h_n(x)$
  +
  +
for $n=2,3,4,5,6$.
  +
  +
==Normalized Hermite==
  +
The original [[Hermite polynomial]]s gave huge values in the interval from $-3$ to $3$. In other to avoid anisotropic scaling of axes,
  +
the normalised hermites are plotted instead of hermites. Normalised hermites $h$ are related with the
  +
[[Hermite polynomial]]s [[HermiteH]] as follows:
  +
  +
$\displaystyle h_n(z)= \frac{1}{\sqrt{N_n}} \mathrm{HermiteH}[n,x]=\frac{H_n(x)}{\sqrt{N_n}}$
  +
  +
$\displaystyle N_n=\int_{-\infty}^{\infty} H_n(z)^2 \, \exp(-x^2)\, \mathrm d x=2^n n! \sqrt{\pi}$
  +
  +
==Implementation of normalised henmites==
  +
// One letter in the name HermiteH is omitted in the routine name to indicate that it is implemented only for very limited number of Hermites,
  +
namely, vrom zero to 13, in order to reserve name '''hermiteh''' for more general procedure, which is not yet in use and therefore is not yet loaded.
  +
  +
<poem><nomathjax><nowiki>
  +
//hermiten.cin (Hermite Normalized)
  +
  +
DB HermiteNo[14]={1, 2, 8, 48, 384, 3840, 46080, 645120, 10321920, 185794560,
  +
3715891200, 81749606400, 1961990553600, 51011754393600};
  +
  +
DB HermitH0[7][7]= // COEFFICIENTS OF EVEN HERMITEH
  +
{{1, 0, 0, 0, 0, 0, 0},
  +
{-2, 4, 0, 0, 0, 0, 0},
  +
{12, -48, 16, 0, 0, 0, 0},
  +
{-120, 720, -480, 64, 0, 0, 0},
  +
{1680, -13440, 13440, -3584, 256, 0, 0},
  +
{-30240, 302400, -403200, 161280, -23040, 1024, 0},
  +
{665280, -7983360, 13305600, -7096320, 1520640, -135168, 4096}};
  +
  +
DB HermitH1[7][7]= // COEFFICIENTS OF ODD HERMITEH
  +
{{2, 0, 0, 0, 0, 0, 0},
  +
{-12, 8, 0, 0, 0, 0, 0},
  +
{120, -160, 32, 0, 0, 0, 0},
  +
{-1680, 3360, -1344, 128, 0, 0, 0},
  +
{30240, -80640, 48384, -9216, 512, 0, 0},
  +
{-665280, 2217600, -1774080, 506880, -56320, 2048, 0},
  +
{17297280, -69189120, 69189120, -26357760,4392960, -319488, 8192}};
  +
  +
DB HermitH(int n,DB x){ int m,M; DB s, xx;
  +
if(n==0) return 1.;
  +
if(n==1) return x+x;
  +
if(n>13) {printf("hermite number %2d is not yet implemented (max. is 13)\n consider to stop..",n); getchar(); return 0;}
  +
xx=x*x; //printf("Hernith called with n=%3d x=%8.2lf\n",n,x);
  +
if(n/2*2==n){M=n/2; s=0.;for(m=M;m>0;m--) {s+=HermitH0[M][m]; s*=xx;}
  +
return (HermitH0[M][0]+s);}
  +
else{ M=(n-1)/2; s=0.; for(m=M;m>0;m--) {s+=HermitH1[M][m]; s*=xx;}
  +
return (HermitH1[M][0]+s)*x; }
  +
}
  +
</nowiki></nomathjax></poem>
  +
  +
== [[C++]] generator of curves==
  +
<poem><nomathjax><nowiki>
  +
#include<math.h>
  +
#include<stdio.h>
  +
#include<stdlib.h>
  +
//#include<limits.h>
  +
#define DB double
  +
#define DO(x,y) for(x=0;x<y;x++)
  +
  +
//#include"her13.cin"
  +
//#include"hermiten.cin"
  +
  +
DB HermiteNo[14]={1, 2, 8, 48, 384, 3840, 46080, 645120, 10321920, 185794560,
  +
3715891200, 81749606400, 1961990553600, 51011754393600};
  +
  +
DB HermitH0[7][7]= // COEFFICIENTS OF EVEN HERMITEH
  +
{{1, 0, 0, 0, 0, 0, 0},
  +
{-2, 4, 0, 0, 0, 0, 0},
  +
{12, -48, 16, 0, 0, 0, 0},
  +
{-120, 720, -480, 64, 0, 0, 0},
  +
{1680, -13440, 13440, -3584, 256, 0, 0},
  +
{-30240, 302400, -403200, 161280, -23040, 1024, 0},
  +
{665280, -7983360, 13305600, -7096320, 1520640, -135168, 4096}};
  +
  +
DB HermitH1[7][7]= // COEFFICIENTS OF ODD HERMITEH
  +
{{2, 0, 0, 0, 0, 0, 0},
  +
{-12, 8, 0, 0, 0, 0, 0},
  +
{120, -160, 32, 0, 0, 0, 0},
  +
{-1680, 3360, -1344, 128, 0, 0, 0},
  +
{30240, -80640, 48384, -9216, 512, 0, 0},
  +
{-665280, 2217600, -1774080, 506880, -56320, 2048, 0},
  +
{17297280, -69189120, 69189120, -26357760,4392960, -319488, 8192}};
  +
  +
DB HermitH(int n,DB x){ int m,M; DB s, xx;
  +
if(n==0) return 1.;
  +
if(n==1) return x+x;
  +
if(n>13) {printf("hermite number %2d is not yet implemented (max. is 13)\n consider to stop..",n); getchar(); return 0;}
  +
xx=x*x; //printf("Hernith called with n=%3d x=%8.2lf\n",n,x);
  +
if(n/2*2==n){M=n/2; s=0.;for(m=M;m>0;m--) {s+=HermitH0[M][m]; s*=xx;}
  +
return (HermitH0[M][0]+s);}
  +
else{ M=(n-1)/2; s=0.; for(m=M;m>0;m--) {s+=HermitH1[M][m]; s*=xx;}
  +
return (HermitH1[M][0]+s)*x; }
  +
}
  +
  +
DB hermiten(int n,DB x){ if(n>13) {printf("hermite number %2d is not yet implemented (max. is 13)\n consider to stop..",n); getchar(); return 0;}
  +
return HermitH(n,x)/sqrt(sqrt(M_PI)*HermiteNo[n]);
  +
}
  +
  +
#include"ado.cin"
  +
  +
int main(){ // printf("%16d %16d\n",INT_MIN,INT_MAX);
  +
int M,m,n; DB x,xx,y,z,s;
  +
FILE *o; o=fopen("46.eps", "w");
  +
ado(o,604,804);
  +
fprintf(o,"302 402 translate 100 100 scale 2 setlinecap 1 setlinejoin\n");
  +
#define M(x,y) fprintf(o,"%6.4lf %6.4lf M\n",x+0., y+0.);
  +
#define L(x,y) fprintf(o,"%6.4lf %6.4lf L\n",x+0., y+0.);
  +
  +
for(m=-3; m<4; m++) {M(m,-3)L(m,3)}
  +
for(n=-3; n<4; n++) {M(-3,n)L(3,n)}
  +
fprintf(o,".01 W 0 0 0 RGB S\n");
  +
  +
DO(n,101){x=.041*(n-50); y= hermiten(2,x); if(n==0)M(x,y) else L(x,y) } fprintf(o,"0 0 0 RGB .016 W S\n ");
  +
DO(n,101){x=.039*(n-50); y= hermiten(3,x); if(n==0)M(x,y) else L(x,y) } fprintf(o,"1 0 0 RGB .016 W S\n ");
  +
DO(n,101){x=.041*(n-50); y= hermiten(4,x); if(n==0)M(x,y) else L(x,y) } fprintf(o,"0 .7 0 RGB .016 W S\n ");
  +
DO(n,101){x=.045*(n-50); y= hermiten(5,x); if(n==0)M(x,y) else L(x,y) } fprintf(o,"0 0 1 RGB .016 W S\n ");
  +
DO(n,201){x=.0248*(n-100); y= hermiten(6,x); if(n==0)M(x,y) else L(x,y) } fprintf(o,".8 0 .9 RGB .016 W S\n ");
  +
  +
fprintf(o,"showpage\n%c%cTrailer\n",'%','%');
  +
fclose(o);
  +
system("epstopdf 46.eps");
  +
system("open 46.pdf");
  +
  +
}
  +
  +
</nowiki></nomathjax></poem>
  +
  +
== [[Latex]] generator of labels==
  +
  +
<poem><nomathjax><nowiki>
  +
\documentclass[12pt]{article}
  +
\usepackage{geometry}
  +
\paperwidth 606pt
  +
\paperheight 710pt
  +
\topmargin -104pt
  +
\oddsidemargin -72pt
  +
\pagestyle{empty}
  +
\usepackage{graphicx}
  +
\parindent 0pt
  +
\textwidth 700px
  +
\textheight 900px
  +
\newcommand \sx {\scalebox}
  +
\begin{document}
  +
\begin{picture}(600,750)
  +
\put(0,0){\includegraphics{46}}
  +
\put(286,744){\sx{2}{$y$}}
  +
\put(286,696){\sx{2}{$3$}}
  +
\put(286,596){\sx{2}{$2$}}
  +
\put(286,495){\sx{2}{$1$}}
  +
\put(270,294){\sx{2}{$-1$}}
  +
\put(270,194){\sx{2}{$-2$}}
  +
\put(86,80){\sx{2}{$-2$}}
  +
\put(186,80){\sx{2}{$-1$}}
  +
\put(298,80){\sx{2}{$0$}}
  +
\put(398,80){\sx{2}{$1$}}
  +
\put(498,80){\sx{2}{$2$}}
  +
\put(591,80){\sx{2}{$x$}}
  +
\end{picture}
  +
\end{document}
  +
</nowiki></nomathjax></poem>
  +
  +
== References==
  +
<references/>
  +
http://mathworld.wolfram.com/HermitePolynomial.html
  +
Weisstein, Eric W. "Hermite Polynomial." From MathWorld--A Wolfram Web Resource.
  +
  +
[[Category:C++]]
  +
[[Category:Explicit plot]]
  +
[[Category:Hermite polynomial]]
  +
[[Category:Latex]]

Latest revision as of 08:37, 1 December 2018

Normalized Hermite polynomials,

$y=h_n(x)$

for $n=2,3,4,5,6$.

Normalized Hermite

The original Hermite polynomials gave huge values in the interval from $-3$ to $3$. In other to avoid anisotropic scaling of axes, the normalised hermites are plotted instead of hermites. Normalised hermites $h$ are related with the Hermite polynomials HermiteH as follows:

$\displaystyle h_n(z)= \frac{1}{\sqrt{N_n}} \mathrm{HermiteH}[n,x]=\frac{H_n(x)}{\sqrt{N_n}}$

$\displaystyle N_n=\int_{-\infty}^{\infty} H_n(z)^2 \, \exp(-x^2)\, \mathrm d x=2^n n! \sqrt{\pi}$

Implementation of normalised henmites

// One letter in the name HermiteH is omitted in the routine name to indicate that it is implemented only for very limited number of Hermites, namely, vrom zero to 13, in order to reserve name hermiteh for more general procedure, which is not yet in use and therefore is not yet loaded.


//hermiten.cin (Hermite Normalized)

DB HermiteNo[14]={1, 2, 8, 48, 384, 3840, 46080, 645120, 10321920, 185794560,
3715891200, 81749606400, 1961990553600, 51011754393600};

DB HermitH0[7][7]= // COEFFICIENTS OF EVEN HERMITEH
{{1, 0, 0, 0, 0, 0, 0},
{-2, 4, 0, 0, 0, 0, 0},
{12, -48, 16, 0, 0, 0, 0},
{-120, 720, -480, 64, 0, 0, 0},
{1680, -13440, 13440, -3584, 256, 0, 0},
{-30240, 302400, -403200, 161280, -23040, 1024, 0},
{665280, -7983360, 13305600, -7096320, 1520640, -135168, 4096}};

DB HermitH1[7][7]= // COEFFICIENTS OF ODD HERMITEH
{{2, 0, 0, 0, 0, 0, 0},
{-12, 8, 0, 0, 0, 0, 0},
{120, -160, 32, 0, 0, 0, 0},
{-1680, 3360, -1344, 128, 0, 0, 0},
{30240, -80640, 48384, -9216, 512, 0, 0},
{-665280, 2217600, -1774080, 506880, -56320, 2048, 0},
{17297280, -69189120, 69189120, -26357760,4392960, -319488, 8192}};

DB HermitH(int n,DB x){ int m,M; DB s, xx;
if(n==0) return 1.;
if(n==1) return x+x;
if(n>13) {printf("hermite number %2d is not yet implemented (max. is 13)\n consider to stop..",n); getchar(); return 0;}
xx=x*x; //printf("Hernith called with n=%3d x=%8.2lf\n",n,x);
if(n/2*2==n){M=n/2; s=0.;for(m=M;m>0;m--) {s+=HermitH0[M][m]; s*=xx;}
                                       return (HermitH0[M][0]+s);}
  else{ M=(n-1)/2; s=0.; for(m=M;m>0;m--) {s+=HermitH1[M][m]; s*=xx;}
                                      return (HermitH1[M][0]+s)*x; }
}

C++ generator of curves


#include<math.h>
#include<stdio.h>
#include<stdlib.h>
//#include<limits.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)

//#include"her13.cin"
//#include"hermiten.cin"

DB HermiteNo[14]={1, 2, 8, 48, 384, 3840, 46080, 645120, 10321920, 185794560,
3715891200, 81749606400, 1961990553600, 51011754393600};

DB HermitH0[7][7]= // COEFFICIENTS OF EVEN HERMITEH
{{1, 0, 0, 0, 0, 0, 0},
{-2, 4, 0, 0, 0, 0, 0},
{12, -48, 16, 0, 0, 0, 0},
{-120, 720, -480, 64, 0, 0, 0},
{1680, -13440, 13440, -3584, 256, 0, 0},
{-30240, 302400, -403200, 161280, -23040, 1024, 0},
{665280, -7983360, 13305600, -7096320, 1520640, -135168, 4096}};

DB HermitH1[7][7]= // COEFFICIENTS OF ODD HERMITEH
{{2, 0, 0, 0, 0, 0, 0},
{-12, 8, 0, 0, 0, 0, 0},
{120, -160, 32, 0, 0, 0, 0},
{-1680, 3360, -1344, 128, 0, 0, 0},
{30240, -80640, 48384, -9216, 512, 0, 0},
{-665280, 2217600, -1774080, 506880, -56320, 2048, 0},
{17297280, -69189120, 69189120, -26357760,4392960, -319488, 8192}};

DB HermitH(int n,DB x){ int m,M; DB s, xx;
if(n==0) return 1.;
if(n==1) return x+x;
if(n>13) {printf("hermite number %2d is not yet implemented (max. is 13)\n consider to stop..",n); getchar(); return 0;}
xx=x*x; //printf("Hernith called with n=%3d x=%8.2lf\n",n,x);
if(n/2*2==n){M=n/2; s=0.;for(m=M;m>0;m--) {s+=HermitH0[M][m]; s*=xx;}
                                       return (HermitH0[M][0]+s);}
  else{ M=(n-1)/2; s=0.; for(m=M;m>0;m--) {s+=HermitH1[M][m]; s*=xx;}
                                      return (HermitH1[M][0]+s)*x; }
}

DB hermiten(int n,DB x){ if(n>13) {printf("hermite number %2d is not yet implemented (max. is 13)\n consider to stop..",n); getchar(); return 0;}
return HermitH(n,x)/sqrt(sqrt(M_PI)*HermiteNo[n]);
}

#include"ado.cin"

int main(){ // printf("%16d %16d\n",INT_MIN,INT_MAX);
int M,m,n; DB x,xx,y,z,s;
FILE *o; o=fopen("46.eps", "w");
ado(o,604,804);
fprintf(o,"302 402 translate 100 100 scale 2 setlinecap 1 setlinejoin\n");
#define M(x,y) fprintf(o,"%6.4lf %6.4lf M\n",x+0., y+0.);
#define L(x,y) fprintf(o,"%6.4lf %6.4lf L\n",x+0., y+0.);

for(m=-3; m<4; m++) {M(m,-3)L(m,3)}
for(n=-3; n<4; n++) {M(-3,n)L(3,n)}
fprintf(o,".01 W 0 0 0 RGB S\n");

DO(n,101){x=.041*(n-50); y= hermiten(2,x); if(n==0)M(x,y) else L(x,y) } fprintf(o,"0 0 0 RGB .016 W S\n ");
DO(n,101){x=.039*(n-50); y= hermiten(3,x); if(n==0)M(x,y) else L(x,y) } fprintf(o,"1 0 0 RGB .016 W S\n ");
DO(n,101){x=.041*(n-50); y= hermiten(4,x); if(n==0)M(x,y) else L(x,y) } fprintf(o,"0 .7 0 RGB .016 W S\n ");
DO(n,101){x=.045*(n-50); y= hermiten(5,x); if(n==0)M(x,y) else L(x,y) } fprintf(o,"0 0 1 RGB .016 W S\n ");
DO(n,201){x=.0248*(n-100); y= hermiten(6,x); if(n==0)M(x,y) else L(x,y) } fprintf(o,".8 0 .9 RGB .016 W S\n ");

fprintf(o,"showpage\n%c%cTrailer\n",'%','%');
fclose(o);
system("epstopdf 46.eps");
system("open 46.pdf");

}

Latex generator of labels


\documentclass[12pt]{article}
\usepackage{geometry}
\paperwidth 606pt
\paperheight 710pt
\topmargin -104pt
\oddsidemargin -72pt
\pagestyle{empty}
\usepackage{graphicx}
\parindent 0pt
\textwidth 700px
\textheight 900px
\newcommand \sx {\scalebox}
\begin{document}
\begin{picture}(600,750)
\put(0,0){\includegraphics{46}}
\put(286,744){\sx{2}{$y$}}
\put(286,696){\sx{2}{$3$}}
\put(286,596){\sx{2}{$2$}}
\put(286,495){\sx{2}{$1$}}
\put(270,294){\sx{2}{$-1$}}
\put(270,194){\sx{2}{$-2$}}
\put(86,80){\sx{2}{$-2$}}
\put(186,80){\sx{2}{$-1$}}
\put(298,80){\sx{2}{$0$}}
\put(398,80){\sx{2}{$1$}}
\put(498,80){\sx{2}{$2$}}
\put(591,80){\sx{2}{$x$}}
\end{picture}
\end{document}

References

http://mathworld.wolfram.com/HermitePolynomial.html Weisstein, Eric W. "Hermite Polynomial." From MathWorld--A Wolfram Web Resource.

File history

Click on a date/time to view the file as it appeared at that time.

Date/TimeThumbnailDimensionsUserComment
current06:12, 1 December 2018Thumbnail for version as of 06:12, 1 December 2018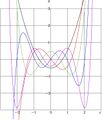1,257 × 1,473 (227 KB)Maintenance script (talk | contribs)Importing image file

You cannot overwrite this file.

The following page uses this file:

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.

If the file has been modified from its original state, some details may not fully reflect the modified file.

Retrieved from "https://mizugadro.mydns.jp/t/index.php?title=File:Hermiten.jpg&oldid=19309"