Difference between revisions of "SuNem"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| Line 1: | Line 1: | ||
| − | [[File:Sunemplo4t.jpg|200px|thumb| |
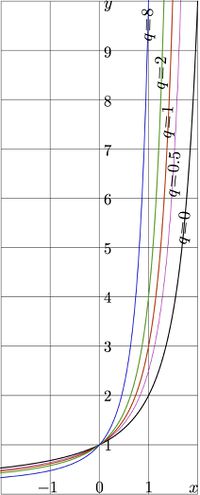
+ | [[File:Sunemplo4t.jpg|200px|thumb|\(y\!=\!\mathrm{SuNem}_{q}(x)\) for various \(q\)]] |
| − | [[File:Sunem0mdp.jpg|200px|thumb| |
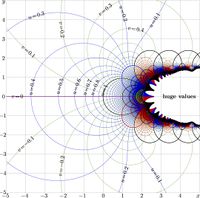
+ | [[File:Sunem0mdp.jpg|200px|thumb|\(u\!+\!\mathrm i v=\mathrm{SuNem}_{0}(x\!+\!\mathrm i y)\)]] |
| − | [[File:Sunem1mdp.jpg|200px|thumb| |
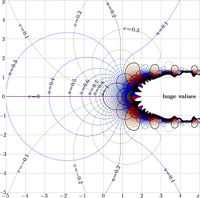
+ | [[File:Sunem1mdp.jpg|200px|thumb|\(u\!+\!\mathrm i v=\mathrm{SuNem}_{1}(x\!+\!\mathrm i y)\)]] |
| − | [[File:Sunem2mdp.jpg|200px|thumb| |
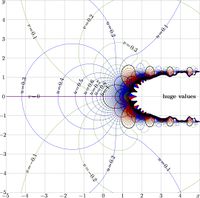
+ | [[File:Sunem2mdp.jpg|200px|thumb|\(u\!+\!\mathrm i v=\mathrm{SuNem}_{2}(x\!+\!\mathrm i y)\)]] |
[[SuNem]] is [[superfunction]] for the [[Nemtsov function]] |
[[SuNem]] is [[superfunction]] for the [[Nemtsov function]] |
||
| − | + | \(\mathrm{Nem}_{q}(z)=z+z^3+qz^4\) |
|
| − | It is assumed, that |
+ | It is assumed, that \(q\!>\!0\), although the formula can be used for some other values of the parameters too. |
SuNem is specific solution of the [[transfer equation]] |
SuNem is specific solution of the [[transfer equation]] |
||
| − | + | \(\mathrm{Nem}_{q}\big( \mathrm{SuNem}_{q}(z)\big)=\mathrm{SuNem}_{q}(z\!+\!1)\). |
|
| − | It is assumed that |
+ | It is assumed that \(\mathrm{SuNem}_{q}(0)=1\). |
Also, the specific asymptotic behaviour at infinity is assumed, |
Also, the specific asymptotic behaviour at infinity is assumed, |
||
| − | + | \(\mathrm{SuNem}_{q}(z) = {\displaystyle \frac{1}{\sqrt{-2z}}}\left(1+O\left(\frac{1}{\sqrt{-2z}} \right)\right)\) |
|
| − | for any fixed phase |
+ | for any fixed phase \(\mathrm{Arg}(z)\) different from zero. |
| − | For any |
+ | For any \(\varepsilon>0\), the formula is valid for any large \(|z|\) such that \(|\mathrm{Arg}(z)|>\varepsilon\). |
| − | Along the real axis, SuNem shows fast growth from zero at |
+ | Along the real axis, SuNem shows fast growth from zero at \(-\infty\) to plus infinity at \(+\infty\). |
==Asymptotic expansion== |
==Asymptotic expansion== |
||
| Line 30: | Line 30: | ||
Function [[SuNem]] is constructed by its asymptotical expansion. |
Function [[SuNem]] is constructed by its asymptotical expansion. |
||
| − | For the superfunction |
+ | For the superfunction \(F\) of the Nemtsov transfer function |
| − | + | \(T=\mathrm{Nem}_{q}\), it can be obtained from the [[transfer equation]] |
|
| − | + | \(T(F(z))=F(z+1)\) |
|
| − | Keping some positive integer mumber |
+ | Keping some positive integer mumber \(M\) of terms, the asymptotic solution can be written as follows: |
| − | + | \(\displaystyle \tilde F(z) = \frac{1}{\sqrt{-2z}} \left(1+ |
|
\frac{P_m(\ln(-z))} |
\frac{P_m(\ln(-z))} |
||
{(-2z)^{m/2}} |
{(-2z)^{m/2}} |
||
| − | \right) |
+ | \right)\) |
| − | where |
+ | where \(\displaystyle P_m(z)=\sum_{n=0}^{\mathrm{IntegerPart}(m/2)} A[m,n]\, z^m\) |
| − | Substitution of |
+ | Substitution of \(\tilde F\) into the transfer equation gives the coefficients \(A\). |
These coefficients can be calculated with the mathematica code below: |
These coefficients can be calculated with the mathematica code below: |
||
<!-- |
<!-- |
||
| − | ==Computation of coefficients |
+ | ==Computation of coefficients \(A\) in the asymptotic expansion== |
| − | In the preliminary version, both parameters, |
+ | In the preliminary version, both parameters, \(p\) and \(q\) are kept in the expansion. |
Methodologically, it is not correct: the expansion can be done simpler for the superfunction for the transfer function with single parameter, |
Methodologically, it is not correct: the expansion can be done simpler for the superfunction for the transfer function with single parameter, |
||
| − | + | \(t_Q(z)=z+z^3+Qz^4=T_{1,Q}(z)\) |
|
with the following relations: |
with the following relations: |
||
| − | + | \(Q=q p^{-3/2}\) |
|
Then |
Then |
||
| − | + | \(T_{p,q}(z)=p^{-1/2} t_{q p^{-3/2}}(p^{1/2} z)\) |
|
| − | The formulas and algorithms will be rewritten for the case |
+ | The formulas and algorithms will be rewritten for the case \(p=1\). |
The superfunctions and abelfunctions can be espressed in the following way: |
The superfunctions and abelfunctions can be espressed in the following way: |
||
| − | + | \(F_{p,q}(z)=\frac{1}{\sqrt{p}} F_{1,q p^{-3/2}}(z)\) |
|
| − | + | \(G_{p,q}(z)=G_{1,q p^{-3/2}}(\sqrt{p} \,z)\) |
|
The figures are supposed to remain the same. Due to simplification of he algorithm, the precision and speed of evaluation of the functions are expected to improve a little bit. |
The figures are supposed to remain the same. Due to simplification of he algorithm, the precision and speed of evaluation of the functions are expected to improve a little bit. |
||
!--> |
!--> |
||
==[[Mathematica]] generator of the algorithm== |
==[[Mathematica]] generator of the algorithm== |
||
| − | The first 18 terms of the asymptotic representation of super function |
+ | The first 18 terms of the asymptotic representation of super function \(F\) can be computed with [[Mathematica]] software, using the code below: |
<poem><nomathjax><nowiki> |
<poem><nomathjax><nowiki> |
||
T[z_]=z+z^3+q z^4 |
T[z_]=z+z^3+q z^4 |
||
| Line 105: | Line 105: | ||
==Evaluation of superfunction== |
==Evaluation of superfunction== |
||
| − | [[File:Sunept.jpg|200px|thumb| |
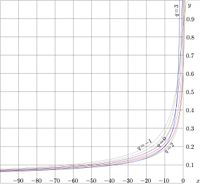
+ | [[File:Sunept.jpg|200px|thumb|\(y\!=\!\mathrm{SuNe}_q(x)\) for \(q=-1, -0.5, 0, 0.5, 1, 2, 3\)]] |
| − | [[File:sunot.jpg|110px|left|thumb|displacement |
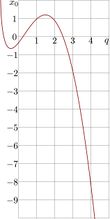
+ | [[File:sunot.jpg|110px|left|thumb|displacement \(x_0\) versus parameter \(q\)]] |
| − | First, the superfunction of the [[Nemtsov function]] is constructed, that does not satisfy the requirement on its value at zero. The idea is to use the asymptotival expansion |
+ | First, the superfunction of the [[Nemtsov function]] is constructed, that does not satisfy the requirement on its value at zero. The idea is to use the asymptotival expansion \(\tilde F\) of the superfunction in the area, where it provides the good approximation, displacing the argument of superfunction into this area with using of the [[transfer equation]]. |
| − | Superfunction |
+ | Superfunction \(\mathrm{SuNe}_q\) of the Nemtsov function \(\mathrm{Nem}_q\) appears as limit |
| − | + | \(\displaystyle |
|
| − | \mathrm{SuNe}_q(z)=\lim_{n \rightarrow \infty} \mathrm{Nem}_q^{\,n} (\tilde F(z\!-\!n)) |
+ | \mathrm{SuNe}_q(z)=\lim_{n \rightarrow \infty} \mathrm{Nem}_q^{\,n} (\tilde F(z\!-\!n))\) |
| − | Explicit plot of function |
+ | Explicit plot of function \(\mathrm{SuNe}_q\) is shown in figure at right for |
| − | + | \(q=-1, -0.5, 0, 0.5, 1, 2, 3~\). |
|
Then, function [[SuNem]] appears with the appropriate displacement of the argument: |
Then, function [[SuNem]] appears with the appropriate displacement of the argument: |
||
| − | + | \(\mathrm{SuNem}_q(z)=\mathrm{SuNe}_q(x_0(q)+z)\) |
|
| − | where displacement |
+ | where displacement \(x_0=x_0(q)\) is real solution of equation \(F_q(x_0)\!=\!1\). This solution is shown in figure at left. |
| − | In order to show the general trend of function |
+ | In order to show the general trend of function \(x_0\), the graphic is extended a little bit into the range of negative \(q\). |
==Inverse function== |
==Inverse function== |
||
Inverse function of [[SuNem]] is function [[AuNem]], that is [[Abel function]] of the [[Nemtsov function]]; |
Inverse function of [[SuNem]] is function [[AuNem]], that is [[Abel function]] of the [[Nemtsov function]]; |
||
| − | in wide range of values of |
+ | in wide range of values of \(z\), it satisfies the [[Abel equation]] |
| − | + | \(\mathrm{AuNem_{q}} \big( \mathrm{Nem_{q}}(z)\big) = \mathrm{Nem_{q}}(z\!+\!1)\) |
|
==Iterates of the Nemtsov function== |
==Iterates of the Nemtsov function== |
||
| Line 134: | Line 134: | ||
With functions [[SuNem]] and [[AuNem]], the iterates of the Nemtsov function can be written as usually: |
With functions [[SuNem]] and [[AuNem]], the iterates of the Nemtsov function can be written as usually: |
||
| − | + | \(\mathrm{Nem}^n(z)=\mathrm{SuNem}(n+\mathrm{AuNem}(z))\) |
|
==References== |
==References== |
||
Latest revision as of 18:44, 30 July 2019
SuNem is superfunction for the Nemtsov function
\(\mathrm{Nem}_{q}(z)=z+z^3+qz^4\)
It is assumed, that \(q\!>\!0\), although the formula can be used for some other values of the parameters too.
SuNem is specific solution of the transfer equation
\(\mathrm{Nem}_{q}\big( \mathrm{SuNem}_{q}(z)\big)=\mathrm{SuNem}_{q}(z\!+\!1)\).
It is assumed that \(\mathrm{SuNem}_{q}(0)=1\).
Also, the specific asymptotic behaviour at infinity is assumed,
\(\mathrm{SuNem}_{q}(z) = {\displaystyle \frac{1}{\sqrt{-2z}}}\left(1+O\left(\frac{1}{\sqrt{-2z}} \right)\right)\)
for any fixed phase \(\mathrm{Arg}(z)\) different from zero.
For any \(\varepsilon>0\), the formula is valid for any large \(|z|\) such that \(|\mathrm{Arg}(z)|>\varepsilon\).
Along the real axis, SuNem shows fast growth from zero at \(-\infty\) to plus infinity at \(+\infty\).
Asymptotic expansion
Function SuNem is constructed by its asymptotical expansion.
For the superfunction \(F\) of the Nemtsov transfer function \(T=\mathrm{Nem}_{q}\), it can be obtained from the transfer equation
\(T(F(z))=F(z+1)\)
Keping some positive integer mumber \(M\) of terms, the asymptotic solution can be written as follows:
\(\displaystyle \tilde F(z) = \frac{1}{\sqrt{-2z}} \left(1+ \frac{P_m(\ln(-z))} {(-2z)^{m/2}} \right)\)
where \(\displaystyle P_m(z)=\sum_{n=0}^{\mathrm{IntegerPart}(m/2)} A[m,n]\, z^m\)
Substitution of \(\tilde F\) into the transfer equation gives the coefficients \(A\). These coefficients can be calculated with the mathematica code below:
Mathematica generator of the algorithm
The first 18 terms of the asymptotic representation of super function \(F\) can be computed with Mathematica software, using the code below:
T[z_]=z+z^3+q z^4
P[m_, L_] := Sum[a[m, n] L^n, {n, 0, IntegerPart[m/2]}]
a[1, 0] = -q; a[2, 0] = 0;
m = 2;
F[m_,z_] = (-2 z)^(-1/2) (1 + Sum[P[n, Log[-z]]/(-2 z)^(n/2), {n, 1, 2}]);
s[m]=Numerator[Normal[Series[(T[F[m,-1/x^2]] - F[m,-1/x^2+1]) 2^((m+1)/2)/x^(m+3), {x,0,0}]]]
sub[m] = Extract[Solve[s[m]==0, a[m,1]], 1];
SUB[m] = sub[m]
For[m = 3, m < 18,
F[m, z_] = ReplaceAll[(-2 z)^(-1/2) (1+Sum[P[n, Log[-z]]/(-2 z)^(n/2), {n,1,m}]), SUB[m-1]];
s[m] = Numerator[Normal[Series[(T[F[m,-1/x^2]]-F[m,-1/x^2+1]) 2^((m+1)/2)/x^(m+3),{x,0,0}]]];
t[m] = Collect[Numerator[ReplaceAll[s[m], Log[x] -> L]], L];
u[m] = Table[
Coefficient[t[m] L, L^n] == 0, {n, 1, 1 + IntegerPart[m/2]}];
tab[m] = Table[a[m, n], {n, 0, IntegerPart[m/2]}];
Print[sub[m] = Simplify[Extract[Solve[u[m], tab[m]], 1]]];
SUB[m] = Join[SUB[m - 1], sub[m]];
m++];
For[m=1, m<18,
For[n=0,n<(m+1)/2,
A[m, n] = TeXForm[ReplaceAll[a[m, n], sub[m]]];
Print["APQ[", m, "][", n, "]=", A[m, n], ";"]
n++];
m++];
Evaluation of superfunction
First, the superfunction of the Nemtsov function is constructed, that does not satisfy the requirement on its value at zero. The idea is to use the asymptotival expansion \(\tilde F\) of the superfunction in the area, where it provides the good approximation, displacing the argument of superfunction into this area with using of the transfer equation.
Superfunction \(\mathrm{SuNe}_q\) of the Nemtsov function \(\mathrm{Nem}_q\) appears as limit
\(\displaystyle \mathrm{SuNe}_q(z)=\lim_{n \rightarrow \infty} \mathrm{Nem}_q^{\,n} (\tilde F(z\!-\!n))\)
Explicit plot of function \(\mathrm{SuNe}_q\) is shown in figure at right for \(q=-1, -0.5, 0, 0.5, 1, 2, 3~\). Then, function SuNem appears with the appropriate displacement of the argument:
\(\mathrm{SuNem}_q(z)=\mathrm{SuNe}_q(x_0(q)+z)\)
where displacement \(x_0=x_0(q)\) is real solution of equation \(F_q(x_0)\!=\!1\). This solution is shown in figure at left. In order to show the general trend of function \(x_0\), the graphic is extended a little bit into the range of negative \(q\).
Inverse function
Inverse function of SuNem is function AuNem, that is Abel function of the Nemtsov function; in wide range of values of \(z\), it satisfies the Abel equation
\(\mathrm{AuNem_{q}} \big( \mathrm{Nem_{q}}(z)\big) = \mathrm{Nem_{q}}(z\!+\!1)\)
Iterates of the Nemtsov function
With functions SuNem and AuNem, the iterates of the Nemtsov function can be written as usually:
\(\mathrm{Nem}^n(z)=\mathrm{SuNem}(n+\mathrm{AuNem}(z))\)
References
Keywords
AuNem, Book, Exotic iterate, Nemtsov function, SuNem, Superfunction