Difference between revisions of "File:SelfCosFTt200.png"
(Importing image file) |
|||
| Line 1: | Line 1: | ||
| + | Two self-fourier functions and their discrete representations and their discrete [[CosFourier]] transforms with $N\!=\!16$ nodes; |
||
| − | Importing image file |
||
| + | : $ \displaystyle f_0(x)=\exp(-x^2/2)$ |
||
| + | : $ \displaystyle f_1(x)=\exp(-x^2/2) (x^4-3x^2)$ |
||
| + | These functions are shown with dotted lines. |
||
| + | |||
| + | The discrete representations at the equidistant grid of $N=16$ nodes with step $d=\sqrt{\pi/N}$ are shown with thick lines. |
||
| + | Their [[DCTI]] transforms are shown with thin black lines. |
||
| + | For these self-fourier functions, the [[DCTI]]s coincide with the originals with 8 decimal digits. |
||
| + | |||
| + | The generator below can be used to test the numeric implementation of the [[CosFourier]] transform. |
||
| + | |||
| + | ==[[C++]] generator of curves== |
||
| + | |||
| + | // Files [[zfour1.cin]], [[zrealft.cin]], [[zcosft1.cin]] should be loaded in the working directory for the compilation of the [[C++]] code below. |
||
| + | |||
| + | // cosft below realizes the [[DCFTI]] transform; the numeration of elements of the input array begins with zero. |
||
| + | |||
| + | #include<math.h> |
||
| + | #include<stdio.h> |
||
| + | #include <stdlib.h> |
||
| + | using namespace std; |
||
| + | #include <complex> |
||
| + | #define z_type complex<double> |
||
| + | #include "zfour1.cin" |
||
| + | #include "zrealft.cin" |
||
| + | #include "zcosft1.cin" |
||
| + | #define DB double |
||
| + | #define Re(x) x.real() |
||
| + | #define Im(x) x.imag() |
||
| + | #define DO(x,y) for(x=0;x<y;x++) |
||
| + | |||
| + | //#include "cosft.cin" |
||
| + | void cosft(z_type a[], int N){ int n; DB d; zcosft1(a-1,N); d=sqrt(2./N); DO(n,N) a[n]*=d; } |
||
| + | // this cosft does the normalized [[DCTI]] |
||
| + | void ado(FILE *O, int X, int Y) |
||
| + | { fprintf(O,"%c!PS-Adobe-2.0 EPSF-2.0\n",'%'); |
||
| + | fprintf(O,"%c%cBoundingBox: 0 0 %d %d\n",'%','%',X,Y); |
||
| + | fprintf(O,"/M {moveto} bind def\n"); |
||
| + | fprintf(O,"/L {lineto} bind def\n"); |
||
| + | fprintf(O,"/S {stroke} bind def\n"); |
||
| + | fprintf(O,"/s {show newpath} bind def\n"); |
||
| + | fprintf(O,"/C {closepath} bind def\n"); |
||
| + | fprintf(O,"/F {fill} bind def\n"); |
||
| + | fprintf(O,"/o {.01 0 360 arc C F} bind def\n"); |
||
| + | fprintf(O,"/times-Roman findfont 20 scalefont setfont\n"); |
||
| + | fprintf(O,"/W {setlinewidth} bind def\n"); |
||
| + | fprintf(O,"/RGB {setrgbcolor} bind def\n");} |
||
| + | |||
| + | // #include "ado.cin" |
||
| + | main(){ z_type *a, *b; int j,N=16; FILE *o; DB x,y,d,xx=x*x; |
||
| + | o=fopen("SelfFourierDCTI.eps","w"); ado(o,55,24); |
||
| + | #define M(x,y) fprintf(o,"%8.4f %8.4f M\n",0.+x,0.+y); |
||
| + | #define L(x,y) fprintf(o,"%8.4f %8.4f L\n",0.+x,0.+y); |
||
| + | #define o(x,y) fprintf(o,"%8.4f %8.4f o\n",0.+x,0.+y); |
||
| + | fprintf(o,"1 13 translate 10 10 scale\n"); |
||
| + | M(0, 1)L(0,-1) M(0,0)L(5,0) fprintf(o,"2 setlinecap .004 W S\n"); |
||
| + | M(0, 1)L(5, 1) fprintf(o,"2 setlinecap .004 W S\n"); |
||
| + | M(0,-1)L(5,-1) fprintf(o,"2 setlinecap .004 W S\n"); |
||
| + | for(j=1;j<11;j++){ M(j,-1)L(j,1);} fprintf(o,"2 setlinecap .004 W S\n"); |
||
| + | d=sqrt(M_PI/N); |
||
| + | a=(z_type *) malloc((size_t)((N+1)*sizeof(z_type))); |
||
| + | b=(z_type *) malloc((size_t)((N+1)*sizeof(z_type))); |
||
| + | for(j=0;j<N+1;j++){x=d*j; xx=x*x; b[j]=a[j]=exp(-.5*x*x)*xx*(xx-3.) ;} |
||
| + | DO(j,N){x=j*d; y=Re(a[j]); if(j==0)M(x,y)else L(x,y) if(x>5) break;} fprintf(o,"0 .9 0 RGB .02 W S\n"); |
||
| + | cosft(a,N); |
||
| + | //zcosft1(a-1,N); for(j=0;j<N+1;j++) a[j]/=sqrt(.5*N); |
||
| + | DO(j,N){x=j*d; y=Re(a[j]); if(j==0)M(x,y)else L(x,y) if(x>5) break;} fprintf(o,"0 0 0 RGB .008 W S\n"); |
||
| + | DO(j,N) a[j]-=b[j]; |
||
| + | for(j=0;j<N+1;j++) printf("%2d %19.16f %19.16f \n",j,a[j].real(),a[j].imag()); |
||
| + | fprintf(o,"0 0 0 RGB\n"); DO(j,120){x=.04*j; xx=x*x; y=exp(-.5*xx)*xx*(xx-3.); o(x,y) if(x>9) break;} |
||
| + | for(j=0;j<N+1;j++){x=d*j; xx=x*x; b[j]=a[j]=exp(-.5*x*x) ;} |
||
| + | DO(j,N){x=j*d; y=Re(a[j]); if(j==0)M(x,y)else L(x,y) if(x>5) break;} fprintf(o,"0 0 1 RGB .016 W S\n"); |
||
| + | cosft(a,N); |
||
| + | //zcosft1(a-1,N); for(j=0;j<N+1;j++) a[j]/=sqrt(.5*N); |
||
| + | DO(j,N){x=j*d; y=Re(a[j]); if(j==0)M(x,y)else L(x,y) if(x>5) break;} fprintf(o,"0 0 0 RGB .005 W S\n"); |
||
| + | DO(j,N) a[j]-=b[j]; |
||
| + | for(j=0;j<N+1;j++) printf("%2d %19.16f %19.16f \n",j,a[j].real(),a[j].imag()); |
||
| + | fprintf(o,"0 0 0 RGB\n"); DO(j,120){x=.04*j; xx=x*x; y=exp(-.5*xx); o(x,y) if(x>9) break;} |
||
| + | free(a); |
||
| + | free(b); |
||
| + | fprintf(o,"showpage\n"); |
||
| + | fprintf(o,"%c%cTrailer\n",'%','%'); |
||
| + | fclose(o); |
||
| + | system("epstopdf SelfFourierDCTI.eps"); |
||
| + | system( "open SelfFourierDCTI.pdf"); |
||
| + | } |
||
| + | |||
| + | ==[[Latex]] generator of labels== |
||
| + | |||
| + | %File [[SelfCosFT.pdf]] should be generated in the working directory with the code above in order to compile the [[Latex]] document below. |
||
| + | |||
| + | <nowiki> |
||
| + | \documentclass[12pt]{article} %<br> |
||
| + | \usepackage{geometry} %<br> |
||
| + | \paperwidth 530pt %<br> |
||
| + | \paperheight 230pt %<br> |
||
| + | \topmargin -92pt %<br> |
||
| + | \oddsidemargin -78pt %<br> |
||
| + | \textwidth 800pt %<br> |
||
| + | \textheight 300pt %<br> |
||
| + | \parindent 0pt %<br> |
||
| + | \pagestyle{empty} %<br> |
||
| + | \usepackage{graphicx} %<br> |
||
| + | \usepackage{epstopdf} %<br> |
||
| + | \newcommand \sx \scalebox %<br> |
||
| + | \begin{document} %<br> |
||
| + | \begin{picture}(520,220) %<br> |
||
| + | %\put(16,0){\sx{10}{\includegraphics{SelfCosFT}}} %<br> |
||
| + | \put(16,0){\sx{10}{\includegraphics{SelfFourierDCTI}}} %<br> |
||
| + | \put(12,223){\sx{1.8}{$1$}} %<br> |
||
| + | \put(12,124){\sx{1.8}{$0$}} %<br> |
||
| + | \put(2, 24){\sx{1.8}{$-\!1$}} %<br> |
||
| + | \put(122, 14){\sx{1.8}{$1$}} %<br> |
||
| + | \put(222, 14){\sx{1.8}{$2$}} %<br> |
||
| + | \put(322, 14){\sx{1.8}{$3$}} %<br> |
||
| + | \put(422, 14){\sx{1.8}{$4$}} %<br> |
||
| + | \put(522, 14){\sx{1.9}{$x$}} %<br> |
||
| + | \put(99, 212){\sx{2}{$f_0(x)$}} %<br> |
||
| + | \put( 58, 102){\sx{2}{$f_1(x)$}} %<br> |
||
| + | %\put( 66, 100){\sx{2}{$\exp(-x^2/2)(x^4-3x^2)$}} %<br> |
||
| + | \end{picture} %<br> |
||
| + | \end{document} %<br> |
||
| + | % </nowiki> |
||
| + | |||
| + | ==References== |
||
| + | <references/> |
||
| + | |||
| + | [[Category:CosFourier]] |
||
| + | [[Category:C++]] |
||
| + | [[Category:Latex]] |
||
| + | [[Category:Self Fourier]] |
||
| + | [[Category:Explicit plot]] |
||
Latest revision as of 09:42, 21 June 2013
Two self-fourier functions and their discrete representations and their discrete CosFourier transforms with $N\!=\!16$ nodes;
- $ \displaystyle f_0(x)=\exp(-x^2/2)$
- $ \displaystyle f_1(x)=\exp(-x^2/2) (x^4-3x^2)$
These functions are shown with dotted lines.
The discrete representations at the equidistant grid of $N=16$ nodes with step $d=\sqrt{\pi/N}$ are shown with thick lines. Their DCTI transforms are shown with thin black lines. For these self-fourier functions, the DCTIs coincide with the originals with 8 decimal digits.
The generator below can be used to test the numeric implementation of the CosFourier transform.
C++ generator of curves
// Files zfour1.cin, zrealft.cin, zcosft1.cin should be loaded in the working directory for the compilation of the C++ code below.
// cosft below realizes the DCFTI transform; the numeration of elements of the input array begins with zero.
#include<math.h>
#include<stdio.h>
#include <stdlib.h>
using namespace std;
#include <complex>
#define z_type complex<double>
#include "zfour1.cin"
#include "zrealft.cin"
#include "zcosft1.cin"
#define DB double
#define Re(x) x.real()
#define Im(x) x.imag()
#define DO(x,y) for(x=0;x<y;x++)
//#include "cosft.cin"
void cosft(z_type a[], int N){ int n; DB d; zcosft1(a-1,N); d=sqrt(2./N); DO(n,N) a[n]*=d; }
// this cosft does the normalized DCTI
void ado(FILE *O, int X, int Y)
{ fprintf(O,"%c!PS-Adobe-2.0 EPSF-2.0\n",'%');
fprintf(O,"%c%cBoundingBox: 0 0 %d %d\n",'%','%',X,Y);
fprintf(O,"/M {moveto} bind def\n");
fprintf(O,"/L {lineto} bind def\n");
fprintf(O,"/S {stroke} bind def\n");
fprintf(O,"/s {show newpath} bind def\n");
fprintf(O,"/C {closepath} bind def\n");
fprintf(O,"/F {fill} bind def\n");
fprintf(O,"/o {.01 0 360 arc C F} bind def\n");
fprintf(O,"/times-Roman findfont 20 scalefont setfont\n");
fprintf(O,"/W {setlinewidth} bind def\n");
fprintf(O,"/RGB {setrgbcolor} bind def\n");}
// #include "ado.cin"
main(){ z_type *a, *b; int j,N=16; FILE *o; DB x,y,d,xx=x*x;
o=fopen("SelfFourierDCTI.eps","w"); ado(o,55,24);
#define M(x,y) fprintf(o,"%8.4f %8.4f M\n",0.+x,0.+y);
#define L(x,y) fprintf(o,"%8.4f %8.4f L\n",0.+x,0.+y);
#define o(x,y) fprintf(o,"%8.4f %8.4f o\n",0.+x,0.+y);
fprintf(o,"1 13 translate 10 10 scale\n");
M(0, 1)L(0,-1) M(0,0)L(5,0) fprintf(o,"2 setlinecap .004 W S\n");
M(0, 1)L(5, 1) fprintf(o,"2 setlinecap .004 W S\n");
M(0,-1)L(5,-1) fprintf(o,"2 setlinecap .004 W S\n");
for(j=1;j<11;j++){ M(j,-1)L(j,1);} fprintf(o,"2 setlinecap .004 W S\n");
d=sqrt(M_PI/N);
a=(z_type *) malloc((size_t)((N+1)*sizeof(z_type)));
b=(z_type *) malloc((size_t)((N+1)*sizeof(z_type)));
for(j=0;j<N+1;j++){x=d*j; xx=x*x; b[j]=a[j]=exp(-.5*x*x)*xx*(xx-3.) ;}
DO(j,N){x=j*d; y=Re(a[j]); if(j==0)M(x,y)else L(x,y) if(x>5) break;} fprintf(o,"0 .9 0 RGB .02 W S\n");
cosft(a,N);
//zcosft1(a-1,N); for(j=0;j<N+1;j++) a[j]/=sqrt(.5*N);
DO(j,N){x=j*d; y=Re(a[j]); if(j==0)M(x,y)else L(x,y) if(x>5) break;} fprintf(o,"0 0 0 RGB .008 W S\n");
DO(j,N) a[j]-=b[j];
for(j=0;j<N+1;j++) printf("%2d %19.16f %19.16f \n",j,a[j].real(),a[j].imag());
fprintf(o,"0 0 0 RGB\n"); DO(j,120){x=.04*j; xx=x*x; y=exp(-.5*xx)*xx*(xx-3.); o(x,y) if(x>9) break;}
for(j=0;j<N+1;j++){x=d*j; xx=x*x; b[j]=a[j]=exp(-.5*x*x) ;}
DO(j,N){x=j*d; y=Re(a[j]); if(j==0)M(x,y)else L(x,y) if(x>5) break;} fprintf(o,"0 0 1 RGB .016 W S\n");
cosft(a,N);
//zcosft1(a-1,N); for(j=0;j<N+1;j++) a[j]/=sqrt(.5*N);
DO(j,N){x=j*d; y=Re(a[j]); if(j==0)M(x,y)else L(x,y) if(x>5) break;} fprintf(o,"0 0 0 RGB .005 W S\n");
DO(j,N) a[j]-=b[j];
for(j=0;j<N+1;j++) printf("%2d %19.16f %19.16f \n",j,a[j].real(),a[j].imag());
fprintf(o,"0 0 0 RGB\n"); DO(j,120){x=.04*j; xx=x*x; y=exp(-.5*xx); o(x,y) if(x>9) break;}
free(a);
free(b);
fprintf(o,"showpage\n");
fprintf(o,"%c%cTrailer\n",'%','%');
fclose(o);
system("epstopdf SelfFourierDCTI.eps");
system( "open SelfFourierDCTI.pdf");
}
Latex generator of labels
%File SelfCosFT.pdf should be generated in the working directory with the code above in order to compile the Latex document below.
\documentclass[12pt]{article} %<br> \usepackage{geometry} %<br> \paperwidth 530pt %<br> \paperheight 230pt %<br> \topmargin -92pt %<br> \oddsidemargin -78pt %<br> \textwidth 800pt %<br> \textheight 300pt %<br> \parindent 0pt %<br> \pagestyle{empty} %<br> \usepackage{graphicx} %<br> \usepackage{epstopdf} %<br> \newcommand \sx \scalebox %<br> \begin{document} %<br> \begin{picture}(520,220) %<br> %\put(16,0){\sx{10}{\includegraphics{SelfCosFT}}} %<br> \put(16,0){\sx{10}{\includegraphics{SelfFourierDCTI}}} %<br> \put(12,223){\sx{1.8}{$1$}} %<br> \put(12,124){\sx{1.8}{$0$}} %<br> \put(2, 24){\sx{1.8}{$-\!1$}} %<br> \put(122, 14){\sx{1.8}{$1$}} %<br> \put(222, 14){\sx{1.8}{$2$}} %<br> \put(322, 14){\sx{1.8}{$3$}} %<br> \put(422, 14){\sx{1.8}{$4$}} %<br> \put(522, 14){\sx{1.9}{$x$}} %<br> \put(99, 212){\sx{2}{$f_0(x)$}} %<br> \put( 58, 102){\sx{2}{$f_1(x)$}} %<br> %\put( 66, 100){\sx{2}{$\exp(-x^2/2)(x^4-3x^2)$}} %<br> \end{picture} %<br> \end{document} %<br> %
References
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 17:50, 20 June 2013 | 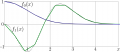 | 1,467 × 637 (100 KB) | Maintenance script (talk | contribs) | Importing image file |
You cannot overwrite this file.
File usage
The following page uses this file: