Difference between revisions of "File:ExpQ2plotT.png"
(Importing image file) |
|||
| Line 1: | Line 1: | ||
| + | [[Explicit plot]] of [[exponential]] to base $b\!=\!\sqrt{2} \approx 1.414213562373095$ |
||
| − | Importing image file |
||
| + | |||
| + | The thick curve: $y=\exp_b(x)$. |
||
| + | |||
| + | The thin line shows the identical funciton, $y\!=\!x$. |
||
| + | |||
| + | The [[fixed point]]s $L\!=\!2$ and $L\!=\!4$ are solutions of the equation |
||
| + | |||
| + | : $\exp_b(L)=L$ |
||
| + | |||
| + | for $b=\sqrt{2}$. |
||
| + | |||
| + | Any of these fixed points can be used to construct a [[superexponential]] to base $\sqrt{2}~$ |
||
| + | <ref> |
||
| + | http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html <br> |
||
| + | http://tori.ils.uec.ac.jp/PAPERS/2010sqrt2.pdf |
||
| + | D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756. |
||
| + | </ref>. |
||
| + | |||
| + | ==References== |
||
| + | <references/> |
||
| + | |||
| + | http://en.wikipedia.org/wiki/Square_root_of_2 |
||
| + | |||
| + | http://en.wikipedia.org/wiki/Exponential_function |
||
| + | |||
| + | ==C++ generator of curves== |
||
| + | #include<math.h> |
||
| + | #include<stdio.h> |
||
| + | #include<stdlib.h> |
||
| + | #define DB double |
||
| + | #define DO(x,y) for(x=0;x<y;x++) |
||
| + | #include "ado.cin" |
||
| + | |||
| + | DB B=sqrt(2.); |
||
| + | |||
| + | main(){ int m,n; double x,y; FILE *o; |
||
| + | o=fopen("ExpQ2plot.eps","w"); ado(o,1204,804); |
||
| + | fprintf(o,"602 2 translate 100 100 scale\n"); |
||
| + | #define M(x,y) fprintf(o,"%6.3f %6.3f M\n",0.+x,0.+y); |
||
| + | #define L(x,y) fprintf(o,"%6.3f %6.3f L\n",0.+x,0.+y); |
||
| + | for(m=-6;m<7;m++) {M(m,0)L(m,8)} |
||
| + | for(m=0;m<9;m++) {M(-6,m)L(6,m)} |
||
| + | fprintf(o,"2 setlinecap .01 W S\n 2 setlinecap 1 setlinejoin \n"); |
||
| + | for(m=0;m<123;m++){x=-6.1+.1*m; y=exp(log(B)*x); if(m==0)M(x,y) else L(x,y);} fprintf(o,".04 W .8 0 0 RGB S\n"); |
||
| + | M(-.1,-.1)L(6.1,6.1) fprintf(o,".016 W 0 0 0 RGB S\n\n"); |
||
| + | fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o); |
||
| + | system("epstopdf ExpQ2plot.eps"); |
||
| + | system( "open ExpQ2plot.pdf"); |
||
| + | getchar(); system("killall Preview");//for mac |
||
| + | } |
||
| + | |||
| + | ==[[Latex]] generator of labels== |
||
| + | |||
| + | %<nowiki> %<br> |
||
| + | % file IterPowPlot.pdf should be generated with the code above in order to compile the Latex document below. %<br> |
||
| + | % Copyleft 2012 by Dmitrii Kouznetsov <br> % |
||
| + | \documentclass[12pt]{article} % <br> |
||
| + | \usepackage{geometry} % <br> |
||
| + | \usepackage{graphicx} % <br> |
||
| + | \usepackage{rotating} % <br> |
||
| + | \paperwidth 1210pt % <br> |
||
| + | \paperheight 840pt % <br> |
||
| + | \topmargin -96pt % <br> |
||
| + | \oddsidemargin -81pt % <br> |
||
| + | \textwidth 1200pt % <br> |
||
| + | \textheight 1100pt % <br> |
||
| + | \pagestyle {empty} % <br> |
||
| + | \newcommand \sx {\scalebox} % <br> |
||
| + | \newcommand \rot {\begin{rotate}} % <br> |
||
| + | \newcommand \ero {\end{rotate}} % <br> |
||
| + | \newcommand \ing {\includegraphics} % <br> |
||
| + | \parindent 0pt% <br> |
||
| + | \pagestyle{empty} % <br> |
||
| + | \begin{document} % <br> |
||
| + | \begin{picture}(1202,804) % <br> |
||
| + | %\put(10,10){\ing{ExpQ2plot}} % <br> |
||
| + | \put(590,792){\sx{4.2}{$y$}} % <br> |
||
| + | \put(590,698){\sx{4.2}{$7$}} % <br> |
||
| + | \put(590,598){\sx{4.2}{$6$}} % <br> |
||
| + | \put(590,498){\sx{4.2}{$5$}} % <br> |
||
| + | \put(590,398){\sx{4.2}{$4$}} % <br> |
||
| + | \put(590,298){\sx{4.2}{$3$}} % <br> |
||
| + | \put(590,198){\sx{4.2}{$2$}} % <br> |
||
| + | \put(590,098){\sx{4.2}{$1$}} % <br> |
||
| + | % <br> |
||
| + | \put(080,-22){\sx{4}{$-5$}} % <br> |
||
| + | \put(180,-22){\sx{4}{$-4$}} % <br> |
||
| + | \put(281,-22){\sx{4}{$-3$}} % <br> |
||
| + | \put(381,-22){\sx{4}{$-2$}} % <br> |
||
| + | \put(482,-22){\sx{4}{$-\!1$}} % <br> |
||
| + | % |
||
| + | \put(603.6,-22){\sx{4}{$0$}} % <br> |
||
| + | \put(703.7,-22){\sx{4}{$1$}} % <br> |
||
| + | \put(803.8,-22){\sx{4}{$2$}} % <br> |
||
| + | \put(903.9,-22){\sx{4}{$3$}} % <br> |
||
| + | \put(1004.0,-22){\sx{4}{$4$}} % <br> |
||
| + | \put(1104.1,-22){\sx{4}{$5$}} % <br> |
||
| + | \put(1192.2,-22){\sx{4.3}{$x$}} % <br> |
||
| + | % <br> |
||
| + | \put(1034,490){\sx{5.6}{\rot{66}$y\!=\!\exp_{_{\!\!\sqrt{2}}}(x)$\ero}} % <br> |
||
| + | \put(1094,444){\sx{5.7}{\rot{45}$y\!=\!x$\ero}} % <br> |
||
| + | %\put(890,316){\sx{4.5}{\rot{45}$y\!=\!x$\ero}} % <br> |
||
| + | %\put(830,164){\sx{4.5}{\rot{44}$y\!=\!\exp_{\sqrt{2}}(x)$\ero}} % <br> |
||
| + | |||
| + | %\put(670,125){\sx{6}{\rot{24}$y\!=\!(\sqrt{2})^x$\ero}} % <br> |
||
| + | %\put(630,164){\sx{6}{\rot{33}$y\!=\!\exp_{\sqrt{2}}(x)$\ero}} % <br> |
||
| + | %\put(690,36){\sx{6}{\rot{45}$y\!=\!x$\ero}} % <br> |
||
| + | \put(10,10){\ing{ExpQ2plot}} % <br> |
||
| + | \end{picture} % <br> |
||
| + | \end{document} % <br> |
||
| + | %</nowiki> |
||
| + | |||
| + | [[Category:Exponential]] |
||
| + | [[Category:Fixed point]] |
||
| + | [[Category:Transfer function]] |
||
| + | [[Category:SuperFunctions]] |
||
| + | [[Category:AbelFunctions]] |
||
| + | [[Category:Explicit plot]] |
||
| + | [[Category:C++]] |
||
| + | [[Category:Latex]] |
||
Revision as of 09:43, 21 June 2013
Explicit plot of exponential to base $b\!=\!\sqrt{2} \approx 1.414213562373095$
The thick curve: $y=\exp_b(x)$.
The thin line shows the identical funciton, $y\!=\!x$.
The fixed points $L\!=\!2$ and $L\!=\!4$ are solutions of the equation
- $\exp_b(L)=L$
for $b=\sqrt{2}$.
Any of these fixed points can be used to construct a superexponential to base $\sqrt{2}~$ [1].
References
- ↑
http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html
http://tori.ils.uec.ac.jp/PAPERS/2010sqrt2.pdf D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.
http://en.wikipedia.org/wiki/Square_root_of_2
http://en.wikipedia.org/wiki/Exponential_function
C++ generator of curves
#include<math.h> #include<stdio.h> #include<stdlib.h> #define DB double #define DO(x,y) for(x=0;x<y;x++) #include "ado.cin"
DB B=sqrt(2.);
main(){ int m,n; double x,y; FILE *o;
o=fopen("ExpQ2plot.eps","w"); ado(o,1204,804);
fprintf(o,"602 2 translate 100 100 scale\n");
#define M(x,y) fprintf(o,"%6.3f %6.3f M\n",0.+x,0.+y);
#define L(x,y) fprintf(o,"%6.3f %6.3f L\n",0.+x,0.+y);
for(m=-6;m<7;m++) {M(m,0)L(m,8)}
for(m=0;m<9;m++) {M(-6,m)L(6,m)}
fprintf(o,"2 setlinecap .01 W S\n 2 setlinecap 1 setlinejoin \n");
for(m=0;m<123;m++){x=-6.1+.1*m; y=exp(log(B)*x); if(m==0)M(x,y) else L(x,y);} fprintf(o,".04 W .8 0 0 RGB S\n");
M(-.1,-.1)L(6.1,6.1) fprintf(o,".016 W 0 0 0 RGB S\n\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
system("epstopdf ExpQ2plot.eps");
system( "open ExpQ2plot.pdf");
getchar(); system("killall Preview");//for mac
}
Latex generator of labels
% %<br> % file IterPowPlot.pdf should be generated with the code above in order to compile the Latex document below. %<br> % Copyleft 2012 by Dmitrii Kouznetsov <br> % \documentclass[12pt]{article} % <br> \usepackage{geometry} % <br> \usepackage{graphicx} % <br> \usepackage{rotating} % <br> \paperwidth 1210pt % <br> \paperheight 840pt % <br> \topmargin -96pt % <br> \oddsidemargin -81pt % <br> \textwidth 1200pt % <br> \textheight 1100pt % <br> \pagestyle {empty} % <br> \newcommand \sx {\scalebox} % <br> \newcommand \rot {\begin{rotate}} % <br> \newcommand \ero {\end{rotate}} % <br> \newcommand \ing {\includegraphics} % <br> \parindent 0pt% <br> \pagestyle{empty} % <br> \begin{document} % <br> \begin{picture}(1202,804) % <br> %\put(10,10){\ing{ExpQ2plot}} % <br> \put(590,792){\sx{4.2}{$y$}} % <br> \put(590,698){\sx{4.2}{$7$}} % <br> \put(590,598){\sx{4.2}{$6$}} % <br> \put(590,498){\sx{4.2}{$5$}} % <br> \put(590,398){\sx{4.2}{$4$}} % <br> \put(590,298){\sx{4.2}{$3$}} % <br> \put(590,198){\sx{4.2}{$2$}} % <br> \put(590,098){\sx{4.2}{$1$}} % <br> % <br> \put(080,-22){\sx{4}{$-5$}} % <br> \put(180,-22){\sx{4}{$-4$}} % <br> \put(281,-22){\sx{4}{$-3$}} % <br> \put(381,-22){\sx{4}{$-2$}} % <br> \put(482,-22){\sx{4}{$-\!1$}} % <br> % \put(603.6,-22){\sx{4}{$0$}} % <br> \put(703.7,-22){\sx{4}{$1$}} % <br> \put(803.8,-22){\sx{4}{$2$}} % <br> \put(903.9,-22){\sx{4}{$3$}} % <br> \put(1004.0,-22){\sx{4}{$4$}} % <br> \put(1104.1,-22){\sx{4}{$5$}} % <br> \put(1192.2,-22){\sx{4.3}{$x$}} % <br> % <br> \put(1034,490){\sx{5.6}{\rot{66}$y\!=\!\exp_{_{\!\!\sqrt{2}}}(x)$\ero}} % <br> \put(1094,444){\sx{5.7}{\rot{45}$y\!=\!x$\ero}} % <br> %\put(890,316){\sx{4.5}{\rot{45}$y\!=\!x$\ero}} % <br> %\put(830,164){\sx{4.5}{\rot{44}$y\!=\!\exp_{\sqrt{2}}(x)$\ero}} % <br> %\put(670,125){\sx{6}{\rot{24}$y\!=\!(\sqrt{2})^x$\ero}} % <br> %\put(630,164){\sx{6}{\rot{33}$y\!=\!\exp_{\sqrt{2}}(x)$\ero}} % <br> %\put(690,36){\sx{6}{\rot{45}$y\!=\!x$\ero}} % <br> \put(10,10){\ing{ExpQ2plot}} % <br> \end{picture} % <br> \end{document} % <br> %
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 17:50, 20 June 2013 | 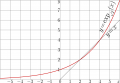 | 2,512 × 1,744 (175 KB) | Maintenance script (talk | contribs) | Importing image file |
You cannot overwrite this file.
File usage
The following page uses this file: