Difference between revisions of "File:Shelre60.png"

From TORI
Jump to navigation Jump to search
(Importing image file)
 
 
Line 1: Line 1:
  +
Explicit plot of [[tetration to Sheldon base]] for real values of the argument.
−
Importing image file
  
  +
  +
Sheldob vase
  +
  +
$b= 1.52598338517+0.0178411853321 \,\mathrm i$.
  +
  +
[[Sheldon Levenstein]] has suggested this number, but he did not provide any way of evaluation of this number; so this value can be considered as exact.
  +
  +
==[[C++]] generator of curves==
  +
  +
Files
  +
[[GLxw2048.inc]] ,
  +
[[TetSheldonIma.inc]] ,
  +
[[ado.cin]] ,
  +
[[conto.cin]] ,
  +
[[filog.cin]]
  +
should be loaded in order to compile the code below:
  +
  +
<poem><nomathjax><nowiki>
  +
#include <math.h>
  +
#include <stdio.h>
  +
#include <stdlib.h>
  +
#define DB double
  +
#define DO(x,y) for(x=0;x<y;x++)
  +
// using namespace std;
  +
#include <complex>
  +
typedef std::complex<double> z_type;
  +
#define Re(x) x.real()
  +
#define Im(x) x.imag()
  +
#define I z_type(0.,1.)
  +
#include "conto.cin"
  +
#include "filog.cin"
  +
z_type b=z_type( 1.5259833851700000, 0.0178411853321000);
  +
z_type a=log(b);
  +
z_type Zo=Filog(a);
  +
z_type Zc=conj(Filog(conj(a)));
  +
DB A=32.;
  +
  +
z_type tetb(z_type z){ int k; DB t; z_type c, cu,cd;
  +
#include "GLxw2048.inc"
  +
int K=2048;
  +
//#include "ima6.inc"
  +
#include "TetSheldonIma.inc"
  +
z_type E[2048],G[2048];
  +
DO(k,K){c=F[k]; E[k]=log(c)/a; G[k]=exp(a*c);}
  +
c=0.;
  +
//z+=z_type( 0.1196573712872846, 0.1299776198056910);
  +
z+=z_type( 0.1196591376539 , 0.1299777213955 );
  +
DO(k,K){t=A*GLx[k];c+=GLw[k]*(G[k]/(z_type( 1.,t)-z)-E[k]/(z_type(-1.,t)-z));}
  +
cu=.5-I/(2.*M_PI)*log( (z_type(1.,-A)+z)/(z_type(1., A)-z) );
  +
cd=.5-I/(2.*M_PI)*log( (z_type(1.,-A)-z)/(z_type(1., A)+z) );
  +
c=c*(A/(2.*M_PI)) +Zo*cu+Zc*cd;
  +
return c;}
  +
  +
z_type TETB(z_type z){ int m,n; DB x=Re(z);
  +
if(x>.51) return exp(a*TETB(z-1.));
  +
if(x<-.51) return log(TETB(z+1.))/a;
  +
return tetb(z);
  +
}
  +
  +
  +
int main(){ int j,k,m,m1,n; DB x,y, p,q, t; z_type z,c,d;
  +
  +
FILE *o;
  +
//o=fopen("sheldonre.eps","w");ado(o,122,122);
  +
// o=fopen("35.eps","w");ado(o,1620,1320);
  +
o=fopen("tetsheldore.eps","w");ado(o,1620,1320);
  +
fprintf(o,"210 610 translate\n 100 100 scale\n");
  +
  +
for(m=-2;m<15;m++){if(m==0){M(m,-6.2)L(m,7.2)} else{M(m,-6)L(m,7)}}
  +
for(n=-7;n<8;n++){ M( -2,n)L(14,n)}
  +
fprintf(o,".008 W 0 0 0 RGB S\n");
  +
  +
DO(m,2410){x=-1.95+.01*m; z=z_type(x,0.);
  +
  +
// c=tetb(z);
  +
c=TETB(z);
  +
  +
p=Re(c); q=Im(c);
  +
y=p; if(m==0) M(x,y) else {if(y<20)L(x,y)}
  +
// printf("%6.2lf %14.10lf %14.10lf\n",x,p,q);
  +
if(x>14.||y>30.) break;
  +
}
  +
fprintf(o,".04 W 0 0 1 RGB S\n");
  +
  +
DO(m,2210){x=-1.99+ .01*m; z=z_type(x,0);
  +
// c=tetb(z);
  +
c=TETB(z);
  +
p=Re(c); q=Im(c);
  +
y=q; if(m==0) M(x,y) else {if(fabs(y)<20) L(x,y)}
  +
// printf("%6.2lf %14.10lf %14.10lf\n",x,p,q);
  +
if(x>14.|| p>1000.) break;
  +
}
  +
fprintf(o,".04 W 1 0 0 RGB S\n");
  +
  +
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
  +
  +
c=TETB(0);
  +
printf("tetb(0)= %16.14lf %16.14lf\n",Re(c),Im(c));
  +
  +
system("epstopdf tetsheldore.eps");
  +
system( "open tetsheldore.pdf");
  +
getchar(); system("killall Preview");
  +
}
  +
  +
</nowiki></nomathjax></poem>
  +
  +
==[[Latex]] generator of labels==
  +
  +
<poem><nomathjax><nowiki>
  +
\documentclass[12pt]{article}
  +
\usepackage{geometry}
  +
\paperwidth 1412pt
  +
\paperheight 1314pt
  +
\textwidth 2000pt
  +
\textheight 2000pt
  +
%\textwidth 700pt
  +
\usepackage{graphics}
  +
% \usepackage{rotate}
  +
\usepackage{rotating}
  +
\newcommand \rot {\begin{rotate}}
  +
\newcommand \ero {\end{rotate}}
  +
\newcommand \sx \scalebox
  +
\newcommand \ing \includegraphics
  +
\parindent 0pt
  +
\topmargin -92pt
  +
\oddsidemargin -80pt
  +
\begin{document}
  +
\begin{picture}(1302,1304)
  +
%\put(0,0){\ing{04}}
  +
%\put(0,0){\ing{tetshelim}}
  +
\put(0,0){\ing{tetsheldore}}
  +
\put(168,1286){\sx{6.7}{$y$}}
  +
\put(170,1190){\sx{6}{$6$}}
  +
\put(170,1090){\sx{6}{$5$}}
  +
\put(170, 990){\sx{6}{$4$}}
  +
\put(170, 890){\sx{6}{$3$}}
  +
\put(170, 790){\sx{6}{$2$}}
  +
\put(170, 690){\sx{6}{$1$}}
  +
%\put(170, 590){\sx{6}{$0$}}
  +
\put(120, 490){\sx{6}{$-1$}}
  +
\put(120, 390){\sx{6}{$-2$}}
  +
\put(120, 290){\sx{6}{$-3$}}
  +
\put(120, 190){\sx{6}{$-4$}}
  +
\put(120, 90){\sx{6}{$-5$}}
  +
  +
\put(60, 550){\sx{6}{$-1$}}
  +
%\put(190, 550){\sx{6}{$0$}}
  +
\put(294, 550){\sx{6}{$1$}}
  +
\put(394, 550){\sx{6}{$2$}}
  +
\put(494, 550){\sx{6}{$3$}}
  +
\put(594, 550){\sx{6}{$4$}}
  +
\put(694, 550){\sx{6}{$5$}}
  +
\put(794, 550){\sx{6}{$6$}}
  +
\put(894, 550){\sx{6}{$7$}}
  +
\put(994, 550){\sx{6}{$8$}}
  +
\put(1094, 550){\sx{6}{$9$}}
  +
\put(1180, 550){\sx{6}{$10$}}
  +
\put(1280, 550){\sx{6}{$11$}}
  +
\put(1374, 550){\sx{6.7}{$x$}}
  +
  +
\put(330,800){\sx{7}{\rot{20}$y\!=\! \Re\big(\mathrm{tet}_b(x)\big)$\ero}}
  +
\put(320,640){\sx{7}{\rot{6}$y\!=\! \Im\big(\mathrm{tet}_b(x)\big)$\ero}}
  +
%\put(320,550){\sx{7}{\rot{2}$y\!=\! \Im\big(\mathrm{tet}_b(x)\big)$\ero}}
  +
\end{picture}
  +
\end{document}
  +
</nowiki></nomathjax></poem>
  +
  +
==References==
  +
<references/>
  +
  +
[[Category:Book]]
  +
[[Category:BookPlot]]
  +
[[Category:C++]]
  +
[[Category:Latex]]
  +
[[Category:Esplicit plot]]
  +
[[Category:Tetration to Sheldon base]]
  +
[[Category:Superfunction]]
  +
[[Category:Superfunctions]]
  +
[[Category:Tetration]]

Latest revision as of 08:51, 1 December 2018

Explicit plot of tetration to Sheldon base for real values of the argument.

Sheldob vase

$b= 1.52598338517+0.0178411853321 \,\mathrm i$.

Sheldon Levenstein has suggested this number, but he did not provide any way of evaluation of this number; so this value can be considered as exact.

C++ generator of curves

Files GLxw2048.inc , TetSheldonIma.inc , ado.cin , conto.cin , filog.cin should be loaded in order to compile the code below:


 #include <math.h>
 #include <stdio.h>
 #include <stdlib.h>
 #define DB double
 #define DO(x,y) for(x=0;x<y;x++)
// using namespace std;
 #include <complex>
 typedef std::complex<double> z_type;
 #define Re(x) x.real()
 #define Im(x) x.imag()
 #define I z_type(0.,1.)
 #include "conto.cin"
 #include "filog.cin"
z_type b=z_type( 1.5259833851700000, 0.0178411853321000);
z_type a=log(b);
z_type Zo=Filog(a);
z_type Zc=conj(Filog(conj(a)));
DB A=32.;

z_type tetb(z_type z){ int k; DB t; z_type c, cu,cd;
#include "GLxw2048.inc"
int K=2048;
//#include "ima6.inc"
#include "TetSheldonIma.inc"
z_type E[2048],G[2048];
DO(k,K){c=F[k]; E[k]=log(c)/a; G[k]=exp(a*c);}
c=0.;
//z+=z_type( 0.1196573712872846, 0.1299776198056910);
z+=z_type( 0.1196591376539 , 0.1299777213955 );
DO(k,K){t=A*GLx[k];c+=GLw[k]*(G[k]/(z_type( 1.,t)-z)-E[k]/(z_type(-1.,t)-z));}
 cu=.5-I/(2.*M_PI)*log( (z_type(1.,-A)+z)/(z_type(1., A)-z) );
 cd=.5-I/(2.*M_PI)*log( (z_type(1.,-A)-z)/(z_type(1., A)+z) );
 c=c*(A/(2.*M_PI)) +Zo*cu+Zc*cd;
 return c;}

z_type TETB(z_type z){ int m,n; DB x=Re(z);
if(x>.51) return exp(a*TETB(z-1.));
if(x<-.51) return log(TETB(z+1.))/a;
return tetb(z);
}


int main(){ int j,k,m,m1,n; DB x,y, p,q, t; z_type z,c,d;

FILE *o;
//o=fopen("sheldonre.eps","w");ado(o,122,122);
// o=fopen("35.eps","w");ado(o,1620,1320);
o=fopen("tetsheldore.eps","w");ado(o,1620,1320);
 fprintf(o,"210 610 translate\n 100 100 scale\n");

 for(m=-2;m<15;m++){if(m==0){M(m,-6.2)L(m,7.2)} else{M(m,-6)L(m,7)}}
 for(n=-7;n<8;n++){ M( -2,n)L(14,n)}
 fprintf(o,".008 W 0 0 0 RGB S\n");

DO(m,2410){x=-1.95+.01*m; z=z_type(x,0.);

// c=tetb(z);
        c=TETB(z);

        p=Re(c); q=Im(c);
        y=p; if(m==0) M(x,y) else {if(y<20)L(x,y)}
// printf("%6.2lf %14.10lf %14.10lf\n",x,p,q);
        if(x>14.||y>30.) break;
        }
 fprintf(o,".04 W 0 0 1 RGB S\n");

DO(m,2210){x=-1.99+ .01*m; z=z_type(x,0);
// c=tetb(z);
        c=TETB(z);
        p=Re(c); q=Im(c);
        y=q; if(m==0) M(x,y) else {if(fabs(y)<20) L(x,y)}
// printf("%6.2lf %14.10lf %14.10lf\n",x,p,q);
        if(x>14.|| p>1000.) break;
        }
 fprintf(o,".04 W 1 0 0 RGB S\n");

 fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);

c=TETB(0);
printf("tetb(0)= %16.14lf %16.14lf\n",Re(c),Im(c));

        system("epstopdf tetsheldore.eps");
        system( "open tetsheldore.pdf");
        getchar(); system("killall Preview");
 }

Latex generator of labels


 \documentclass[12pt]{article}
 \usepackage{geometry}
 \paperwidth 1412pt
 \paperheight 1314pt
 \textwidth 2000pt
 \textheight 2000pt
 %\textwidth 700pt
 \usepackage{graphics}
% \usepackage{rotate}
\usepackage{rotating}
 \newcommand \rot {\begin{rotate}}
 \newcommand \ero {\end{rotate}}
 \newcommand \sx \scalebox
 \newcommand \ing \includegraphics
\parindent 0pt
\topmargin -92pt
\oddsidemargin -80pt
\begin{document}
\begin{picture}(1302,1304)
%\put(0,0){\ing{04}}
%\put(0,0){\ing{tetshelim}}
\put(0,0){\ing{tetsheldore}}
\put(168,1286){\sx{6.7}{$y$}}
\put(170,1190){\sx{6}{$6$}}
\put(170,1090){\sx{6}{$5$}}
\put(170, 990){\sx{6}{$4$}}
\put(170, 890){\sx{6}{$3$}}
\put(170, 790){\sx{6}{$2$}}
\put(170, 690){\sx{6}{$1$}}
%\put(170, 590){\sx{6}{$0$}}
\put(120, 490){\sx{6}{$-1$}}
\put(120, 390){\sx{6}{$-2$}}
\put(120, 290){\sx{6}{$-3$}}
\put(120, 190){\sx{6}{$-4$}}
\put(120, 90){\sx{6}{$-5$}}

\put(60, 550){\sx{6}{$-1$}}
%\put(190, 550){\sx{6}{$0$}}
\put(294, 550){\sx{6}{$1$}}
\put(394, 550){\sx{6}{$2$}}
\put(494, 550){\sx{6}{$3$}}
\put(594, 550){\sx{6}{$4$}}
\put(694, 550){\sx{6}{$5$}}
\put(794, 550){\sx{6}{$6$}}
\put(894, 550){\sx{6}{$7$}}
\put(994, 550){\sx{6}{$8$}}
\put(1094, 550){\sx{6}{$9$}}
\put(1180, 550){\sx{6}{$10$}}
\put(1280, 550){\sx{6}{$11$}}
\put(1374, 550){\sx{6.7}{$x$}}

\put(330,800){\sx{7}{\rot{20}$y\!=\! \Re\big(\mathrm{tet}_b(x)\big)$\ero}}
\put(320,640){\sx{7}{\rot{6}$y\!=\! \Im\big(\mathrm{tet}_b(x)\big)$\ero}}
%\put(320,550){\sx{7}{\rot{2}$y\!=\! \Im\big(\mathrm{tet}_b(x)\big)$\ero}}
\end{picture}
\end{document}

References

File history

Click on a date/time to view the file as it appeared at that time.

Date/TimeThumbnailDimensionsUserComment
current06:14, 1 December 2018Thumbnail for version as of 06:14, 1 December 2018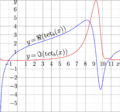1,172 × 1,090 (142 KB)Maintenance script (talk | contribs)Importing image file

You cannot overwrite this file.

The following page uses this file:

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.

If the file has been modified from its original state, some details may not fully reflect the modified file.

Retrieved from "https://mizugadro.mydns.jp/t/index.php?title=File:Shelre60.png&oldid=21441"