Difference between revisions of "File:Sqrt2sufuplot.png"
(Importing image file) |
|||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| + | <div style="margin:-18px -14px 0px -200px; background-color:#fff"> |
||
| − | Importing image file |
||
| + | <div style="margin:0px 0px 0px 30px; line-height:1.2em"><br> |
||
| + | Four superexponentials to base \(b=\sqrt{2}\) |
||
| + | |||
| + | They are real-holomorphic solutions \(F\) of the transfer equation |
||
| + | |||
| + | \( \exp_b(F(z))=F(z\!+\!1) \) |
||
| + | |||
| + | with different values at zero and different asymptotic properties. |
||
| + | |||
| + | Along the real axis, functions |
||
| + | \(F_{2,3} \) and |
||
| + | \(F_{4,3} \) coincide with 24 decimal figures; |
||
| + | the deviation |
||
| + | |||
| + | \( d_{42}(x)=F_{4,3}(x)-F_{2,3}(x) \) |
||
| + | |||
| + | scaled with factor \(10^{24} \) is shown with violet sinusoidal bell. |
||
| + | |||
| + | ==Usage== |
||
| + | This image is used in book [[Суперфункции]] (2014, In Russian) <ref name="r"> |
||
| + | https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0 <br> |
||
| + | http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf <br> |
||
| + | http://mizugadro.mydns.jp/BOOK/202.pdf |
||
| + | Д.Кузнецов. Суперфункции. [[Lambert Academic Publishing]], 2014. |
||
| + | </ref> is figure 16.10, page 237. |
||
| + | |||
| + | This image is used in book [[Superfunctions]] (2020, in English) <ref name="e"> |
||
| + | https://www.morebooks.de/store/gb/book/superfunctions/isbn/978-620-2-67286-3 <br> |
||
| + | https://mizugadro.mydns.jp/BOOK/466.pdf |
||
| + | D.Kouznetsov. [[Superfunctions]]. [[Lambert Academic Publishing]], 2020. |
||
| + | </ref> as figure 16.9, page 232. |
||
| + | |||
| + | The English version <ref name="e"/> happen to be better, than the Russian <ref name="r"/> one; so, <ref name="e"/> can be recommended for the description. |
||
| + | |||
| + | This image is used also in article with Henryk Trappmann |
||
| + | <ref> |
||
| + | http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html <br> |
||
| + | http://mizugadro.mydns.jp/PAPERS/2010sqrt2.pdf offprint |
||
| + | D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756. |
||
| + | </ref>, Fig.3, page 1740. <br> |
||
| + | Henryk had asked the Editor to consider superexponentials to base \( b \!=\!\sqrt{2} \); |
||
| + | this pic had been plotted to satisfy his curiosity. |
||
| + | |||
| + | See the description in the cited literature. |
||
| + | The description happens to be a little bit long; so, it is not reproduced here). |
||
| + | |||
| + | ==Refereces== |
||
| + | <references/> |
||
| + | |||
| + | |||
| + | ==[[C++]] generator of the curves== |
||
| + | Files [[ado.cin]], |
||
| + | [[conto.cin]], |
||
| + | [[sqrt2f21e.cin]], |
||
| + | [[sqrt2f23e.cin]], |
||
| + | [[sqrt2f43e.cin]], |
||
| + | [[sqrt2f45e.cin]] |
||
| + | should be loaded in order to compile the code below. |
||
| + | |||
| + | <poem><nomathjax><nowiki> |
||
| + | |||
| + | #include <math.h> |
||
| + | #include <stdio.h> |
||
| + | #include <stdlib.h> |
||
| + | #define DB double |
||
| + | #define DO(x,y) for(x=0;x<y;x++) |
||
| + | #include <complex> |
||
| + | typedef std::complex<double> z_type; |
||
| + | #define Re(x) x.real() |
||
| + | #define Im(x) x.imag() |
||
| + | #define I z_type(0.,1.) |
||
| + | #include "ado.cin" |
||
| + | #include "sqrt2f21e.cin" |
||
| + | #include "sqrt2f23e.cin" |
||
| + | #include "sqrt2f43e.cin" |
||
| + | #include "sqrt2f45e.cin" |
||
| + | //#include "superex.cin" |
||
| + | //#include "slog14128.cin" |
||
| + | #include "difapro.cin" |
||
| + | int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d; |
||
| + | // FILE *o;o=fopen("rearea1.eps","w"); ado(o,202,148); |
||
| + | FILE *o;o=fopen("sqrt23.eps","w"); ado(o,202,148); |
||
| + | fprintf(o,"101 41 translate\n 10 10 scale\n"); |
||
| + | #define M(x,y) fprintf(o,"%7.4f %7.4f M\n",0.+x,0.+y); |
||
| + | #define L(x,y) fprintf(o,"%7.4f %7.4f L\n",0.+x,0.+y); |
||
| + | M(0,-4.06)L(0,10.06) |
||
| + | M(-10.06,0)L(10.06,0) |
||
| + | fprintf(o,".03 W S\n"); |
||
| + | for(n=-10;n<11;n++){if(n!=0){M(n,0)L(n,-.1)}} |
||
| + | for(n= -4;n<11;n++){if(n!=0){M(0,n)L(-.1,n)}} |
||
| + | fprintf(o,".03 W S\n"); |
||
| + | M(-2,-4)L(-2,0) |
||
| + | M(0,2)L(10,2) |
||
| + | //M(-2,2)L(4,-4) |
||
| + | M(-10,4)L(0,4) |
||
| + | fprintf(o,".01 W S\n"); |
||
| + | |||
| + | fprintf(o,"1 setlinejoin 2 setlinecap\n"); |
||
| + | for(m=0;m< 84; m+=4) { x=-1.84+.01*m; z=x; y=Re(F21E(z)); if(m==0) M(x,y) else L(x,y)} |
||
| + | for(m=0;m<511; m+=10){ x=-1. +.01*m; z=x; y=Re(F21E(z)); L(x,y)} |
||
| + | for(m=520;m<1101;m+=20){ x=-1. +.01*m; z=x; y=Re(F21E(z)); L(x,y)} |
||
| + | fprintf(o,".05 W 0 0 1 RGB S\n"); |
||
| + | |||
| + | for(m=0;m<201;m+=5) { x=-10+.1*m; z=x; y=Re(F23E(z)); if(m==0) M(x,y) else L(x,y)} |
||
| + | fprintf(o,".05 W 0 .8 0 RGB S\n"); |
||
| + | |||
| + | //for(m=0;m<201;m+=5) { x=-10+.1*m; z=x; y=Re(F43E(z)); if(m==0) M(x,y) else L(x,y)} |
||
| + | //fprintf(o,".02 W .5 0 .5 RGB S\n"); |
||
| + | |||
| + | for(m=0;m<166;m+=5) { x=-10+sqrt(1.*m); z=x; y=Re(F45E(z)); if(m==0) M(x,y) else L(x,y)} |
||
| + | fprintf(o,".03 W 1 0 0 RGB S\n"); |
||
| + | |||
| + | //for(m=0;m<386;m+=5) { x=-1.984+.01*m; z=x; y=Re(FSEXP(z)); if(m==0) M(x,y) else L(x,y)} |
||
| + | //fprintf(o,".07 W 0 1 1 RGB S\n"); |
||
| + | |||
| + | //for(m=0;m<145;m+=2) { y=-4+.1*m; z=z_type(y,0.); x=Re(FSLOG(z)); if(m==0) M(x,y) else L(x,y)} |
||
| + | //fprintf(o,".012 W 0 0 0 RGB S\n"); |
||
| + | |||
| + | DO(m,502){ x=-10.+.04*m; |
||
| + | z=z_type(x,0.); |
||
| + | c=difapro(z); |
||
| + | y=Re(c)*1.e24; |
||
| + | if(m==0) M(x,y) else L(x,y)} |
||
| + | fprintf(o,".02 W .6 0 .6 RGB S\n"); |
||
| + | |||
| + | |||
| + | fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o); |
||
| + | system("epstopdf sqrt23.eps"); |
||
| + | system( "open sqrt23.pdf"); |
||
| + | getchar(); system("killall Preview"); // For macintosh |
||
| + | } |
||
| + | </nowiki></nomathjax></poem> |
||
| + | |||
| + | ==[[Latex]] generator of the labels== |
||
| + | |||
| + | <poem><nomathjax><nowiki> |
||
| + | \documentclass[12pt]{article} |
||
| + | \usepackage{geometry} |
||
| + | \usepackage{graphicx} |
||
| + | \usepackage{rotating} |
||
| + | \paperwidth 424pt |
||
| + | \paperheight 302pt |
||
| + | \topmargin -106pt |
||
| + | \oddsidemargin -73pt |
||
| + | \textwidth 1064pt |
||
| + | \textheight 1060pt |
||
| + | \pagestyle {empty} |
||
| + | \newcommand \sx {\scalebox} |
||
| + | \newcommand \rot {\begin{rotate}} |
||
| + | \newcommand \ero {\end{rotate}} |
||
| + | \newcommand \ing {\includegraphics} |
||
| + | \parindent 0pt |
||
| + | \pagestyle{empty} |
||
| + | \begin{document} \sx{2.1}{\begin{picture}(146,142) |
||
| + | %\put(10,10){\ing{IterPowPlot}} |
||
| + | %\put(40,40){\ing{Itereq2tlo}} |
||
| + | \put(0,0){\ing{sqrt23}} |
||
| + | \put(95,139){\sx{.7}{$y$}} |
||
| + | \put(95,119){\sx{.6}{$8$}} |
||
| + | \put(95, 99){\sx{.6}{$6$}} |
||
| + | \put(95, 79){\sx{.6}{$4$}} |
||
| + | \put(95, 59){\sx{.6}{$2$}} |
||
| + | \put(91, 19){\sx{.6}{$-2$}} |
||
| + | \put( 17,35){\sx{.6}{$-\!8$}} |
||
| + | \put( 37,35){\sx{.6}{$-\!6$}} |
||
| + | \put( 57,35){\sx{.6}{$-\!4$}} |
||
| + | \put( 77,35){\sx{.6}{$-\!2$}} |
||
| + | \put(120,35){\sx{.6}{$2$}} |
||
| + | \put(140,35){\sx{.6}{$4$}} |
||
| + | \put(160,35){\sx{.6}{$6$}} |
||
| + | \put(180,35){\sx{.6}{$8$}} |
||
| + | \put(197.6,35){\sx{.7}{$x$}} |
||
| + | % |
||
| + | \put(110,93){\sx{.6}{$y\!=\!F_{4,5}(x)\!=\!\mathrm{SuExp}_{\sqrt{2},5}(x)$}} |
||
| + | %\put(116, 88){\sx{.7}{$y\!=\!\mathrm{tet}(x)$}} |
||
| + | \put(126, 69){\sx{.6}{$y\!=\!F_{2,3}(x)$, $y\!=\!F_{4,3}(x)$}} |
||
| + | \put(126, 54){\sx{.6}{$y\!=\!F_{2,1}(x)\!=\!\mathrm{tet}_{\sqrt{2}}(x)$}} |
||
| + | %\put(108, 44){\sx{.7}{$y\!=\!10^{24}w(x)$}} |
||
| + | %\enp} |
||
| + | \put(126,44){\sx{.6}{$y\!=\!10^{24} d_{42}(x)$}} |
||
| + | \end{picture}} |
||
| + | \end{document} |
||
| + | |||
| + | </nowiki></nomathjax></poem> |
||
| + | |||
| + | [[Category:Base sqrt2]] |
||
| + | [[Category:Book]] |
||
| + | [[Category:BookPlot]] |
||
| + | [[Category:C++]] |
||
| + | [[Category:Explicit plot]] |
||
| + | [[Category:Exp]] |
||
| + | [[Category:Generator]] |
||
| + | [[Category:Latex]] |
||
| + | [[Category:Superfunction]] |
||
| + | [[Category:Tetration]] |
||
Latest revision as of 10:11, 10 June 2022
Four superexponentials to base \(b=\sqrt{2}\)
They are real-holomorphic solutions \(F\) of the transfer equation
\( \exp_b(F(z))=F(z\!+\!1) \)
with different values at zero and different asymptotic properties.
Along the real axis, functions \(F_{2,3} \) and \(F_{4,3} \) coincide with 24 decimal figures; the deviation
\( d_{42}(x)=F_{4,3}(x)-F_{2,3}(x) \)
scaled with factor \(10^{24} \) is shown with violet sinusoidal bell.
Usage
This image is used in book Суперфункции (2014, In Russian) [1] is figure 16.10, page 237.
This image is used in book Superfunctions (2020, in English) [2] as figure 16.9, page 232.
The English version [2] happen to be better, than the Russian [1] one; so, [2] can be recommended for the description.
This image is used also in article with Henryk Trappmann
[3], Fig.3, page 1740.
Henryk had asked the Editor to consider superexponentials to base \( b \!=\!\sqrt{2} \);
this pic had been plotted to satisfy his curiosity.
See the description in the cited literature. The description happens to be a little bit long; so, it is not reproduced here).
Refereces
- ↑ 1.0 1.1
https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf
http://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Publishing, 2014. - ↑ 2.0 2.1 2.2
https://www.morebooks.de/store/gb/book/superfunctions/isbn/978-620-2-67286-3
https://mizugadro.mydns.jp/BOOK/466.pdf D.Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020. - ↑
http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html
http://mizugadro.mydns.jp/PAPERS/2010sqrt2.pdf offprint D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.
C++ generator of the curves
Files ado.cin, conto.cin, sqrt2f21e.cin, sqrt2f23e.cin, sqrt2f43e.cin, sqrt2f45e.cin should be loaded in order to compile the code below.
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
#include <complex>
typedef std::complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "ado.cin"
#include "sqrt2f21e.cin"
#include "sqrt2f23e.cin"
#include "sqrt2f43e.cin"
#include "sqrt2f45e.cin"
//#include "superex.cin"
//#include "slog14128.cin"
#include "difapro.cin"
int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;
// FILE *o;o=fopen("rearea1.eps","w"); ado(o,202,148);
FILE *o;o=fopen("sqrt23.eps","w"); ado(o,202,148);
fprintf(o,"101 41 translate\n 10 10 scale\n");
#define M(x,y) fprintf(o,"%7.4f %7.4f M\n",0.+x,0.+y);
#define L(x,y) fprintf(o,"%7.4f %7.4f L\n",0.+x,0.+y);
M(0,-4.06)L(0,10.06)
M(-10.06,0)L(10.06,0)
fprintf(o,".03 W S\n");
for(n=-10;n<11;n++){if(n!=0){M(n,0)L(n,-.1)}}
for(n= -4;n<11;n++){if(n!=0){M(0,n)L(-.1,n)}}
fprintf(o,".03 W S\n");
M(-2,-4)L(-2,0)
M(0,2)L(10,2)
//M(-2,2)L(4,-4)
M(-10,4)L(0,4)
fprintf(o,".01 W S\n");
fprintf(o,"1 setlinejoin 2 setlinecap\n");
for(m=0;m< 84; m+=4) { x=-1.84+.01*m; z=x; y=Re(F21E(z)); if(m==0) M(x,y) else L(x,y)}
for(m=0;m<511; m+=10){ x=-1. +.01*m; z=x; y=Re(F21E(z)); L(x,y)}
for(m=520;m<1101;m+=20){ x=-1. +.01*m; z=x; y=Re(F21E(z)); L(x,y)}
fprintf(o,".05 W 0 0 1 RGB S\n");
for(m=0;m<201;m+=5) { x=-10+.1*m; z=x; y=Re(F23E(z)); if(m==0) M(x,y) else L(x,y)}
fprintf(o,".05 W 0 .8 0 RGB S\n");
//for(m=0;m<201;m+=5) { x=-10+.1*m; z=x; y=Re(F43E(z)); if(m==0) M(x,y) else L(x,y)}
//fprintf(o,".02 W .5 0 .5 RGB S\n");
for(m=0;m<166;m+=5) { x=-10+sqrt(1.*m); z=x; y=Re(F45E(z)); if(m==0) M(x,y) else L(x,y)}
fprintf(o,".03 W 1 0 0 RGB S\n");
//for(m=0;m<386;m+=5) { x=-1.984+.01*m; z=x; y=Re(FSEXP(z)); if(m==0) M(x,y) else L(x,y)}
//fprintf(o,".07 W 0 1 1 RGB S\n");
//for(m=0;m<145;m+=2) { y=-4+.1*m; z=z_type(y,0.); x=Re(FSLOG(z)); if(m==0) M(x,y) else L(x,y)}
//fprintf(o,".012 W 0 0 0 RGB S\n");
DO(m,502){ x=-10.+.04*m;
z=z_type(x,0.);
c=difapro(z);
y=Re(c)*1.e24;
if(m==0) M(x,y) else L(x,y)}
fprintf(o,".02 W .6 0 .6 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
system("epstopdf sqrt23.eps");
system( "open sqrt23.pdf");
getchar(); system("killall Preview"); // For macintosh
}
Latex generator of the labels
\documentclass[12pt]{article}
\usepackage{geometry}
\usepackage{graphicx}
\usepackage{rotating}
\paperwidth 424pt
\paperheight 302pt
\topmargin -106pt
\oddsidemargin -73pt
\textwidth 1064pt
\textheight 1060pt
\pagestyle {empty}
\newcommand \sx {\scalebox}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\newcommand \ing {\includegraphics}
\parindent 0pt
\pagestyle{empty}
\begin{document} \sx{2.1}{\begin{picture}(146,142)
%\put(10,10){\ing{IterPowPlot}}
%\put(40,40){\ing{Itereq2tlo}}
\put(0,0){\ing{sqrt23}}
\put(95,139){\sx{.7}{$y$}}
\put(95,119){\sx{.6}{$8$}}
\put(95, 99){\sx{.6}{$6$}}
\put(95, 79){\sx{.6}{$4$}}
\put(95, 59){\sx{.6}{$2$}}
\put(91, 19){\sx{.6}{$-2$}}
\put( 17,35){\sx{.6}{$-\!8$}}
\put( 37,35){\sx{.6}{$-\!6$}}
\put( 57,35){\sx{.6}{$-\!4$}}
\put( 77,35){\sx{.6}{$-\!2$}}
\put(120,35){\sx{.6}{$2$}}
\put(140,35){\sx{.6}{$4$}}
\put(160,35){\sx{.6}{$6$}}
\put(180,35){\sx{.6}{$8$}}
\put(197.6,35){\sx{.7}{$x$}}
%
\put(110,93){\sx{.6}{$y\!=\!F_{4,5}(x)\!=\!\mathrm{SuExp}_{\sqrt{2},5}(x)$}}
%\put(116, 88){\sx{.7}{$y\!=\!\mathrm{tet}(x)$}}
\put(126, 69){\sx{.6}{$y\!=\!F_{2,3}(x)$, $y\!=\!F_{4,3}(x)$}}
\put(126, 54){\sx{.6}{$y\!=\!F_{2,1}(x)\!=\!\mathrm{tet}_{\sqrt{2}}(x)$}}
%\put(108, 44){\sx{.7}{$y\!=\!10^{24}w(x)$}}
%\enp}
\put(126,44){\sx{.6}{$y\!=\!10^{24} d_{42}(x)$}}
\end{picture}}
\end{document}
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 06:14, 1 December 2018 | 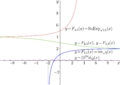 | 3,520 × 2,507 (408 KB) | Maintenance script (talk | contribs) | Importing image file |
You cannot overwrite this file.
File usage
The following page uses this file: