Difference between revisions of "Квадратный корень из факториала"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| Line 1: | Line 1: | ||
| − | [[File:SquareRootOfFactorial.png|400px|right|thumb| |
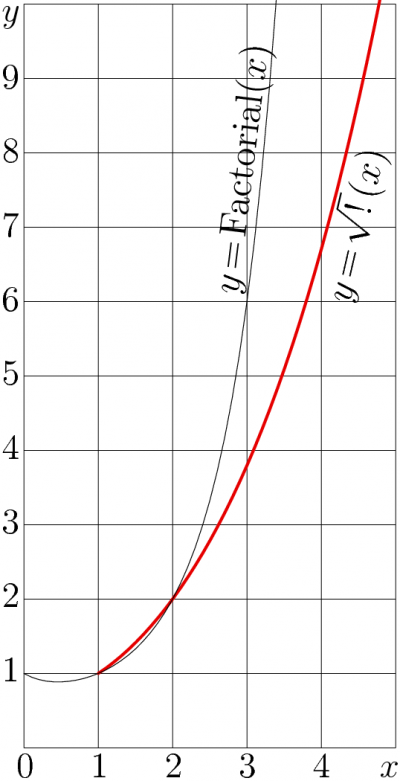
+ | [[File:SquareRootOfFactorial.png|400px|right|thumb| \(y\!=\! x!\) и \(y\!=\!\sqrt{!\,}(x)\) как функции от \(x\)]] |
| − | Квадратный корень из факториала ([[Square root of factorial]]), то есть |
+ | Квадратный корень из факториала ([[Square root of factorial]]), то есть \(\sqrt{\,!\,}\) - голоморфная функкция \(f\) такая, что ее вторая итерация дает факториал, то есть |
| − | : |
+ | : \(f(f(z))=z!\) |
Таким образом, корень из факториала является половинной итерацией факториала, то есть |
Таким образом, корень из факториала является половинной итерацией факториала, то есть |
||
| − | : |
+ | : \(\sqrt{\,!\,}(х)=\mathrm{Factorial}^{1/2}(x)\) |
==Путаница== |
==Путаница== |
||
Иногда выражение |
Иногда выражение |
||
| − | + | \(\sqrt{\,!\,}(х)\) путают с выражениями |
|
| − | + | \(\sqrt{х!\,}\) и |
|
| − | + | \(\sqrt{х}\,!\), хотя это совсем разные функции. Для избежания путаницы, лучше пользоваться буквенной формой имени функций, например, \(\mathrm{Factorial}(x)\). |
|
Тогда "250! лет" не будут производить впечатления |
Тогда "250! лет" не будут производить впечатления |
||
Factorial(250) лет <!-- |
Factorial(250) лет <!-- |
||
= |
= |
||
3232856260909107732320814552024368470994843717673780666747942427112823747555111209488817915371028199450928507353189432926730931712808990822791030279071281921676527240189264733218041186261006832925365133678939089569935713530175040513178760077247933065402339006164825552248819436572586057399222641254832982204849137721776650641276858807153128978777672951913990844377478702589172973255150283241787320658188482062478582659808848825548800000000000000000000000000000000000000000000000000000000000000 лет!--> |
3232856260909107732320814552024368470994843717673780666747942427112823747555111209488817915371028199450928507353189432926730931712808990822791030279071281921676527240189264733218041186261006832925365133678939089569935713530175040513178760077247933065402339006164825552248819436572586057399222641254832982204849137721776650641276858807153128978777672951913990844377478702589172973255150283241787320658188482062478582659808848825548800000000000000000000000000000000000000000000000000000000000000 лет!--> |
||
| − | + | \(\approx 3.232856260909\times 10^{492}\) лет. |
|
==История== |
==История== |
||
| − | Примерно s 1950 года, название этой функции является эмблемой Физического факультета [[МГУ]], хотя в ХХ веке не было алгоритмов для вычисления той функции и считалось, что выражение |
+ | Примерно s 1950 года, название этой функции является эмблемой Физического факультета [[МГУ]], хотя в ХХ веке не было алгоритмов для вычисления той функции и считалось, что выражение \(\sqrt{\,!\,}\) не имеет математического смысля. Разумеется, эта функция может эффективно вычисляться через СуперФакториал и АбельФакториал с помощью метода регулярных итераций. После построения этого метода, с 2011 года, имя этой функции использовано в качестве элемента эмблемы [[ТОРИ]] (корень из факториала на фоне алого круга), показываемой в левом верхнем углу каждой страницы. |
Описание свойств корня из факториала имеется в английской версии этой статьи, см. [[Square root of factorial]]. |
Описание свойств корня из факториала имеется в английской версии этой статьи, см. [[Square root of factorial]]. |
||
Latest revision as of 18:33, 30 July 2019
Квадратный корень из факториала (Square root of factorial), то есть \(\sqrt{\,!\,}\) - голоморфная функкция \(f\) такая, что ее вторая итерация дает факториал, то есть
- \(f(f(z))=z!\)
Таким образом, корень из факториала является половинной итерацией факториала, то есть
- \(\sqrt{\,!\,}(х)=\mathrm{Factorial}^{1/2}(x)\)
Путаница
Иногда выражение \(\sqrt{\,!\,}(х)\) путают с выражениями \(\sqrt{х!\,}\) и \(\sqrt{х}\,!\), хотя это совсем разные функции. Для избежания путаницы, лучше пользоваться буквенной формой имени функций, например, \(\mathrm{Factorial}(x)\). Тогда "250! лет" не будут производить впечатления Factorial(250) лет \(\approx 3.232856260909\times 10^{492}\) лет.
История
Примерно s 1950 года, название этой функции является эмблемой Физического факультета МГУ, хотя в ХХ веке не было алгоритмов для вычисления той функции и считалось, что выражение \(\sqrt{\,!\,}\) не имеет математического смысля. Разумеется, эта функция может эффективно вычисляться через СуперФакториал и АбельФакториал с помощью метода регулярных итераций. После построения этого метода, с 2011 года, имя этой функции использовано в качестве элемента эмблемы ТОРИ (корень из факториала на фоне алого круга), показываемой в левом верхнем углу каждой страницы.
Описание свойств корня из факториала имеется в английской версии этой статьи, см. Square root of factorial.
Ссылки
http://www.springerlink.com/content/qt31671237421111/fulltext.pdf?page=1 D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12
http://zhurnal.lib.ru/img/g/garik/dubinushka/index.shtml Logo of the Physics Department of the Moscow State University. (In Russian);
http://ofvp.phys.msu.ru/pdf/Kandidov_70.pdf: В.П.Кандидов. О времени и о себе. По итогам студенческого голосования победителями оказались значок с изображением рычага, поднимающего Землю, и нынешний с хорошо известной эмблемой в виде корня из факториала, вписанными в букву Ф. Этот значок, созданный студентом кафедры биофизики А.Сарвазяном, привлекал своей простотой и выразительностью. Тогда эмблема этого значка подверглась жесткой критике со стороны руководства факультета, поскольку она не имеет физического смысла, математически абсурдна и идеологически бессодержательна.
http://nauka.relis.ru/11/0412/11412002.htm ПЕРВОМУ УНИВЕРСИТЕТУ СТРАНЫ - 250! На значке физфака в букву "Ф" вписано стилизованное изображение корня из факториала (√!) - выражение, математического смысла не имеющее.
http://www.digizeitschriften.de/dms/img/?PPN=GDZPPN002175851 H.Kneser. Reelle analytische Lösungen der Gleichung φ(φ(x))=ex. Equationes Mathematicae, Journal fur die reine und angewandte Mathematik {\bf 187} 56–67 (1950)
http://www.springerlink.com/content/u712vtp4122544x4 D.Kouznetsov. Holomorphic extension of the logistic sequence. Moscow University Physics Bulletin, 2010, No.2, p.91-98
http://www.springerlink.com/content/u7327836m2850246/ H.Trappmann, D.Kouznetsov. Uniqueness of Analytic Abel Functions in Absence of a Real Fixed Point. Aequationes Mathematicae, v.81, p.65-76 (2011)