Difference between revisions of "Linear fuction"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| Line 1: | Line 1: | ||
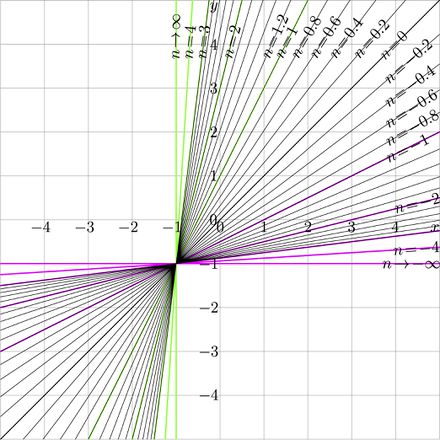
| − | [[File:Itelin125T.jpg|440px|thumb|Iterates of |
+ | [[File:Itelin125T.jpg|440px|thumb|Iterates of \(T(z)=A+Bz~\) at \(~A\!=\!1\), \(B\!=\!2~\); \(~y=T^n(x)~\) versus \(x\) for various \(n\)]] |
[[Linear function]] is function that can be represented in form |
[[Linear function]] is function that can be represented in form |
||
| − | + | \((1) ~ ~ ~ T(z)=A+B z\) |
|
| − | where |
+ | where \(A\) and \(B\) are constants (for example some complex numbers) |
==Abelfunction and Superfunction== |
==Abelfunction and Superfunction== |
||
| − | [[Superfunction]] |
+ | [[Superfunction]] \(F\) for the linear function \(T\) by (1) can be written as follows: |
| − | + | \((2) ~ ~ ~ \displaystyle F(z)= A \frac{1-B^z}{1-B}\) |
|
The corresponding [[Abel function]] can be expressed as follows: |
The corresponding [[Abel function]] can be expressed as follows: |
||
| − | + | \((3) ~ ~ ~ \displaystyle G(z)= \log_B\Big(1+\frac{B-1}{A}z \big)\) |
|
==Iterates== |
==Iterates== |
||
| Line 21: | Line 21: | ||
the superfunction and the Abel function in the standard way, |
the superfunction and the Abel function in the standard way, |
||
| − | + | \((4) ~ ~ ~ \displaystyle T^n(z)=F(n+G(z))\) |
|
| − | Substitution of the Superfunction |
+ | Substitution of the Superfunction \(F\) by (2) and the Abel function \(G\) by (3) into equation (4) gives aslo linear function |
| − | + | \((5) ~ ~ ~ \displaystyle T^n(z)= |
|
| − | \frac{-A+B^n\Big( A+(-1+B) z\Big)}{-1+B}=A \frac {B^n-1}{B-1} +B^n z |
+ | \frac{-A+B^n\Big( A+(-1+B) z\Big)}{-1+B}=A \frac {B^n-1}{B-1} +B^n z\) |
| − | with new parameters |
+ | with new parameters \(A \frac {B^n-1}{B-1}\) instead of \(A\) in (1) and |
| − | + | \(B^n\) instead of \(B\). With this representation, the number \(n\) of iteration has no need to be integer. As other holomophic functions, the linear function can be iterated even complex number of times. |
|
==References== |
==References== |
||
Latest revision as of 18:43, 30 July 2019
Linear function is function that can be represented in form
\((1) ~ ~ ~ T(z)=A+B z\)
where \(A\) and \(B\) are constants (for example some complex numbers)
Abelfunction and Superfunction
Superfunction \(F\) for the linear function \(T\) by (1) can be written as follows:
\((2) ~ ~ ~ \displaystyle F(z)= A \frac{1-B^z}{1-B}\)
The corresponding Abel function can be expressed as follows:
\((3) ~ ~ ~ \displaystyle G(z)= \log_B\Big(1+\frac{B-1}{A}z \big)\)
Iterates
Iterate of the linear function can be expressed through the superfunction and the Abel function in the standard way,
\((4) ~ ~ ~ \displaystyle T^n(z)=F(n+G(z))\)
Substitution of the Superfunction \(F\) by (2) and the Abel function \(G\) by (3) into equation (4) gives aslo linear function
\((5) ~ ~ ~ \displaystyle T^n(z)= \frac{-A+B^n\Big( A+(-1+B) z\Big)}{-1+B}=A \frac {B^n-1}{B-1} +B^n z\)
with new parameters \(A \frac {B^n-1}{B-1}\) instead of \(A\) in (1) and \(B^n\) instead of \(B\). With this representation, the number \(n\) of iteration has no need to be integer. As other holomophic functions, the linear function can be iterated even complex number of times.
References
Keywords
Abel function, Holomorphic function, Iteration, Superfunction