Difference between revisions of "Holomorphic extension of the Collatz subsequence"

From TORI
Jump to navigation Jump to search
 
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)")
 
Line 16: Line 16:
 
Journal of Integer Sequences, Vol. 11 (2008), Article 08.4.7.
  
Journal of Integer Sequences, Vol. 11 (2008), Article 08.4.7.
 
</ref>; this subsequence
 
</ref>; this subsequence
−
can be defined through the transfer function $g$ of the Collatz sequence.
 +
can be defined through the transfer function \(g\) of the Collatz sequence.
−
For integer values of $n$, the Collatx transfer function
 +
For integer values of \(n\), the Collatx transfer function
−
: $g(n)=\left\{
+
: \(g(n)=\left\{
 
\begin{array}{c}
 
\begin{array}{c}
 
n/2 , \mathrm{ ~~if~~ } n/2 \in \mathbb N \\
  
n/2 , \mathrm{ ~~if~~ } n/2 \in \mathbb N \\
Line 24: Line 24:
 
\end{array}
  
\end{array}
 
\right.
  
\right.
−
$
+
\)
   
−
The subsequence is defined with the transfer function $h=g^2$ , that means second iteration of $g$; for integer $n$,
+
The subsequence is defined with the transfer function \(h=g^2\) , that means second iteration of \(g\); for integer \(n\),
−
: $h(n)=g(g(n))$
 +
: \(h(n)=g(g(n))\)
   
−
The holomorphic extension of $h$ is suggested.
 +
The holomorphic extension of \(h\) is suggested.
−
The holomorphic extension $F$ of the sequence, generated with such a transfer function, is constructed,
 +
The holomorphic extension \(F\) of the sequence, generated with such a transfer function, is constructed,
−
: $h(F(z))=F(z\!+\!1)$
 +
: \(h(F(z))=F(z\!+\!1)\)
   
 
==Extension of the transfer function==
  
==Extension of the transfer function==
−
[[File:plog4.png|right|200px|thumb|$y=h(x)$ and $y=x$ in the $x,y$ plane]]
 +
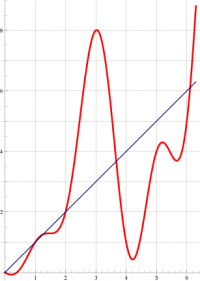
[[File:plog4.png|right|200px|thumb|\(y=h(x)\) and \(y=x\) in the \(x,y\) plane]]
−
The simple expression exactly fit values of $g(g(n))$ at integer values of $n$:<br>
 +
The simple expression exactly fit values of \(g(g(n))\) at integer values of \(n\):<br>
−
$h(n)=\frac{1}{4} \left(4 n-(3 n\!+\!2)
 +
\(h(n)=\frac{1}{4} \left(4 n-(3 n\!+\!2)
 
\sin \left(\frac{\pi n}{2}\right)-(n\!+\!1) \cos
  
\sin \left(\frac{\pi n}{2}\right)-(n\!+\!1) \cos
 
\left(\frac{\pi n}{2}\right)-(2 n\!+\!1) \cos
  
\left(\frac{\pi n}{2}\right)-(2 n\!+\!1) \cos
 
(\pi n)+2\right)
  
(\pi n)+2\right)
  +
\)
−
$
  
   
−
This representation allows the straightforward extension for the complex $n$.
+
This representation allows the straightforward extension for the complex \(n\).
   
−
Function $h$ has several real [[fixed point]]s; in particular, 0,1,2.
+
Function \(h\) has several real [[fixed point]]s; in particular, 0,1,2.
 
Fixed point 2 is used below for the construction of the [[superfunction]]
  
Fixed point 2 is used below for the construction of the [[superfunction]]
   
 
==Regular iteration==
  
==Regular iteration==
−
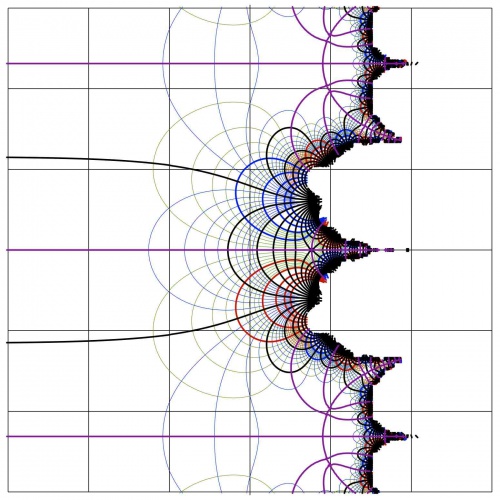
[[File:File-Sirakuse03a.jpg|right|500px|thumb|Complex map of function $F$]]
 +
[[File:File-Sirakuse03a.jpg|right|500px|thumb|Complex map of function \(F\)]]
   
 
Use of the [[regular iteration]] for the construction of a [[superfunction]] for a holomorphic transfer function at its fixed point is pretty straightforward
  
Use of the [[regular iteration]] for the construction of a [[superfunction]] for a holomorphic transfer function at its fixed point is pretty straightforward
Line 60: Line 60:
 
http://www.springerlink.com/content/qt31671237421111/fulltext.pdf?page=1
  
http://www.springerlink.com/content/qt31671237421111/fulltext.pdf?page=1
 
D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12.
  
D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12.
−
</ref>. Choose the fixed point 2, $h(2)=2$.
 +
</ref>. Choose the fixed point 2, \(h(2)=2\).
−
In order to construct the [[superfunction]] $F$ of the transfer function $h$ at this fixed point, seethe the solution of equation
 +
In order to construct the [[superfunction]] \(F\) of the transfer function \(h\) at this fixed point, seethe the solution of equation
−
: $h(F(z))-F(z\!+\!1)=0$
 +
: \(h(F(z))-F(z\!+\!1)=0\)
 
in th following form:
  
in th following form:
−
: $F(z)=2+\varepsilon
 +
: \(F(z)=2+\varepsilon
 
+ a_2 \varepsilon^2
  
+ a_2 \varepsilon^2
 
+ a_3 \varepsilon^3
  
+ a_3 \varepsilon^3
 
+ a_4 \varepsilon^4
  
+ a_4 \varepsilon^4
−
+ . . . $
 +
+ . . . \)
−
where $\varepsilon=\exp(kz)$ , and $k\in \mathbb R$ is constant. Then,
 +
where \(\varepsilon=\exp(kz)\) , and \(k\in \mathbb R\) is constant. Then,
−
: $F(z\!+\!1)=2+q\varepsilon
 +
: \(F(z\!+\!1)=2+q\varepsilon
 
+ a_2 q^2\varepsilon^2
  
+ a_2 q^2\varepsilon^2
 
+ a_3 q^3\varepsilon^3
  
+ a_3 q^3\varepsilon^3
−
+ a_4 q^4\varepsilon^4 + . . . $
 +
+ a_4 q^4\varepsilon^4 + . . . \)
−
where $q=\exp(k)$.
 +
where \(q=\exp(k)\).
   
−
Sibstitution the expressions for $F(k)$ and $F(k\!+\!1)$ into the equation above, and the expansion to the [[Taylor series]] with respect to $\varepsilon$ gives the equation for $k$ and the chain of equations for the coefficients $a$,
 +
Sibstitution the expressions for \(F(k)\) and \(F(k\!+\!1)\) into the equation above, and the expansion to the [[Taylor series]] with respect to \(\varepsilon\) gives the equation for \(k\) and the chain of equations for the coefficients \(a\),
 
determining
  
determining
−
: $q=3/4+\pi$~,~ id est, $k=\log(3/4+\pi)\approx 1.3588184963564824177$
 +
: \(q=3/4+\pi\)~,~ id est, \(k=\log(3/4+\pi)\approx 1.3588184963564824177\)
−
: $a_2=\frac{12 \pi +17 \pi ^2}{2 \left(-3+8 \pi +16 \pi ^2\right)} \approx 0.57063727286450673698$
 +
: \(a_2=\frac{12 \pi +17 \pi ^2}{2 \left(-3+8 \pi +16 \pi ^2\right)} \approx 0.57063727286450673698\)
−
: $a_3=-\frac{2 \pi ^2
 +
: \(a_3=-\frac{2 \pi ^2
 
\left(-369-1404 \pi -1171
  
\left(-369-1404 \pi -1171
 
\pi ^2+64 \pi ^3\right)}{3
  
\pi ^2+64 \pi ^3\right)}{3
 
(7+4 \pi ) \left(-3+8 \pi
  
(7+4 \pi ) \left(-3+8 \pi
 
+16 \pi ^2\right)^2}
  
+16 \pi ^2\right)^2}
−
\approx 0.14888910250614386537$
 +
\approx 0.14888910250614386537\)
 
and so on.
  
and so on.
   
−
The approximation for $F$ above is food while $-\Re(z)$ is large; for other values of $z$, the representation
 +
The approximation for \(F\) above is food while \(-\Re(z)\) is large; for other values of \(z\), the representation
−
: $F(z)=h^n(F(z-n))$
 +
: \(F(z)=h^n(F(z-n))\)
−
should be used at the integer $n$ large enough to get the required precision.
 +
should be used at the integer \(n\) large enough to get the required precision.
   
−
==Properties of $F$==
 +
==Properties of \(F\)==
   
−
Function $F$ has no singularities, it is [[entire function]].
 +
Function \(F\) has no singularities, it is [[entire function]].
   
−
Function $F$ is periodic, its period $T=\frac{2 \pi \rm i}{k}=
 +
Function \(F\) is periodic, its period \(T=\frac{2 \pi \rm i}{k}=
−
\frac{2 \pi \rm i}{\ln(3/4+\pi)}\approx 4.6240063143291284184~ \mathrm i$.
 +
\frac{2 \pi \rm i}{\ln(3/4+\pi)}\approx 4.6240063143291284184~ \mathrm i\).
   
−
In the direction of negative real part of the argument, $F$ exponentially approached the fixed point 2 of the transfer function $h$.
 +
In the direction of negative real part of the argument, \(F\) exponentially approached the fixed point 2 of the transfer function \(h\).
   
−
At the real axis, the function grows monotonically, from 2, approaching the next [[fixed point]] of function $h$ (which is approximately 3.7).
 +
At the real axis, the function grows monotonically, from 2, approaching the next [[fixed point]] of function \(h\) (which is approximately 3.7).
   
−
As any other entire function, $F$ gets all the values (except, perhaps, one; for function $F$ it is 0), including all the integer values.
 +
As any other entire function, \(F\) gets all the values (except, perhaps, one; for function \(F\) it is 0), including all the integer values.
   
 
==Conclusion==
  
==Conclusion==

Latest revision as of 18:25, 30 July 2019

UNDER CONSTRUCTION !!!

Abstract

The Terras Sequence [1][2][3] is subsequence of the Collatz sequense [4]; this subsequence can be defined through the transfer function \(g\) of the Collatz sequence. For integer values of \(n\), the Collatx transfer function

\(g(n)=\left\{ \begin{array}{c} n/2 , \mathrm{ ~~if~~ } n/2 \in \mathbb N \\ (3n\!+\!1)/2 ~ \mathrm{~~over-vice} \end{array} \right. \)

The subsequence is defined with the transfer function \(h=g^2\) , that means second iteration of \(g\); for integer \(n\),

\(h(n)=g(g(n))\)

The holomorphic extension of \(h\) is suggested. The holomorphic extension \(F\) of the sequence, generated with such a transfer function, is constructed,

\(h(F(z))=F(z\!+\!1)\)

Extension of the transfer function

\(y=h(x)\) and \(y=x\) in the \(x,y\) plane

The simple expression exactly fit values of \(g(g(n))\) at integer values of \(n\):
\(h(n)=\frac{1}{4} \left(4 n-(3 n\!+\!2) \sin \left(\frac{\pi n}{2}\right)-(n\!+\!1) \cos \left(\frac{\pi n}{2}\right)-(2 n\!+\!1) \cos (\pi n)+2\right) \)

This representation allows the straightforward extension for the complex \(n\).

Function \(h\) has several real fixed points; in particular, 0,1,2. Fixed point 2 is used below for the construction of the superfunction

Regular iteration

Complex map of function \(F\)

Use of the regular iteration for the construction of a superfunction for a holomorphic transfer function at its fixed point is pretty straightforward [5][6][7]. Choose the fixed point 2, \(h(2)=2\). In order to construct the superfunction \(F\) of the transfer function \(h\) at this fixed point, seethe the solution of equation

\(h(F(z))-F(z\!+\!1)=0\)

in th following form:

\(F(z)=2+\varepsilon + a_2 \varepsilon^2 + a_3 \varepsilon^3 + a_4 \varepsilon^4 + . . . \)

where \(\varepsilon=\exp(kz)\) , and \(k\in \mathbb R\) is constant. Then,

\(F(z\!+\!1)=2+q\varepsilon + a_2 q^2\varepsilon^2 + a_3 q^3\varepsilon^3 + a_4 q^4\varepsilon^4 + . . . \)

where \(q=\exp(k)\).

Sibstitution the expressions for \(F(k)\) and \(F(k\!+\!1)\) into the equation above, and the expansion to the Taylor series with respect to \(\varepsilon\) gives the equation for \(k\) and the chain of equations for the coefficients \(a\), determining

\(q=3/4+\pi\)~,~ id est, \(k=\log(3/4+\pi)\approx 1.3588184963564824177\)
\(a_2=\frac{12 \pi +17 \pi ^2}{2 \left(-3+8 \pi +16 \pi ^2\right)} \approx 0.57063727286450673698\)
\(a_3=-\frac{2 \pi ^2 \left(-369-1404 \pi -1171 \pi ^2+64 \pi ^3\right)}{3 (7+4 \pi ) \left(-3+8 \pi +16 \pi ^2\right)^2} \approx 0.14888910250614386537\)

and so on.

The approximation for \(F\) above is food while \(-\Re(z)\) is large; for other values of \(z\), the representation

\(F(z)=h^n(F(z-n))\)

should be used at the integer \(n\) large enough to get the required precision.

Properties of \(F\)

Function \(F\) has no singularities, it is entire function.

Function \(F\) is periodic, its period \(T=\frac{2 \pi \rm i}{k}= \frac{2 \pi \rm i}{\ln(3/4+\pi)}\approx 4.6240063143291284184~ \mathrm i\).

In the direction of negative real part of the argument, \(F\) exponentially approached the fixed point 2 of the transfer function \(h\).

At the real axis, the function grows monotonically, from 2, approaching the next fixed point of function \(h\) (which is approximately 3.7).

As any other entire function, \(F\) gets all the values (except, perhaps, one; for function \(F\) it is 0), including all the integer values.

Conclusion

In the similar way, the inverse of the Collatz sequence can be generalized. The holomorphic extensions can be use in the proof of the Collatz conjectures.

References

  1. ↑ http://mathworld.wolfram.com/CollatzProblem.html
  2. ↑ Terras, R. "A Stopping Time Problem on the Positive Integers." Acta Arith. 30, 241-252, 1976.
  3. ↑ Terras, R. "On the Existence of a Density." Acta Arith. 35, 101-102, 1979.
  4. ↑ http://www.cs.uwaterloo.ca/journals/JIS/VOL11/Snapp/snapp.pdf Bart Snapp and Matt Tracy. The Collatz Problem and Analogues. Journal of Integer Sequences, Vol. 11 (2008), Article 08.4.7.
  5. ↑ http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.
  6. ↑ http://www.springerlink.com/content/u712vtp4122544x4 D.Kouznetsov. Holomorphic extension of the logistic sequence. Moscow University Physics Bulletin, 2010, No.2, p.91-98.
  7. ↑ http://www.springerlink.com/content/qt31671237421111/fulltext.pdf?page=1 D.Kouznetsov, H.Trappmann. Superfunctions and square root of factorial. Moscow University Physics Bulletin, 2010, v.65, No.1, p.6-12.

http://en.wikipedia.org/wiki/Collatz_conjecture Collatz Conjecture Calculation Center

http://www-personal.ksu.edu/~kconrow/ Ken Conrow Home Page. Collatz 3n+1 Problem Structure

http://members.chello.nl/k.ijntema/

http://wn.com/Collatz_conjecture (video)

http://preprint.math.uni-hamburg.de/public/papers/hbam/hbam2011-09.pdf Gerhard Opfer. An analytic approach to the Collatz 3n + 1 Problem. Preprint Nr. 2011-09, May 2011.

Retrieved from "https://mizugadro.mydns.jp/t/index.php?title=Holomorphic_extension_of_the_Collatz_subsequence&oldid=27978"