Difference between revisions of "ArcLogisticSequence"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| Line 1: | Line 1: | ||
| − | [[File:LogiarcT300.png|160px|thumb| |
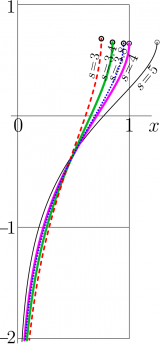
+ | [[File:LogiarcT300.png|160px|thumb|\(\mathrm{ArcLogisticSequance}_s(x)\) versus \(x\) for various \(s\)]] |
| − | [[File:Logi2d3T1500.png|360px|thumb| |
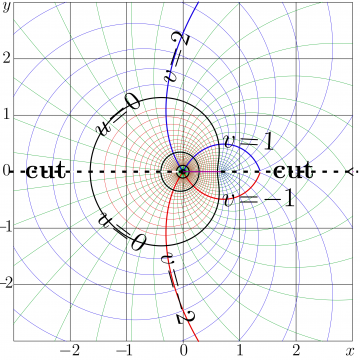
+ | [[File:Logi2d3T1500.png|360px|thumb| \(u\!+\! \mathrm i v= \mathrm{ArcLogisticSequence}_3(x\!+\!\mathrm i y)\) in the \(x\), \(y\) plane]] |
| − | [[ArcLogisticSequence]] |
+ | [[ArcLogisticSequence]]\(_s\) is holomorphic function, inverse of function [[LogisticSequence]], |
| − | where |
+ | where \(s\) is parameter; usually it is assumed that it has real values. In order to avoid confusions, words [[Arc]], [[Logistic]] and [[Sequence]] in the name should be written without spacebars: in the [[common sense]] |
and the [[mathematic notation]]s, the space is usually interpreted as operation of multiplication or [[combination of functions]]. |
and the [[mathematic notation]]s, the space is usually interpreted as operation of multiplication or [[combination of functions]]. |
||
ArcLogisticSequence is [[Abel function]] for the [[Logistic operator]] as the transfer function, |
ArcLogisticSequence is [[Abel function]] for the [[Logistic operator]] as the transfer function, |
||
| − | : |
+ | :\(\!\!\!\!\!\!\!\!\!\! (1) ~ ~ ~ T(z)=\mathrm{LogisticOperator}_s(z)= s\, z\, (1\!-\!z)\) |
Tthe ArcLogisticSequence satisfies the [[Abel equation]] |
Tthe ArcLogisticSequence satisfies the [[Abel equation]] |
||
| − | : |
+ | :\(\!\!\!\!\!\!\!\!\!\! (2) ~ ~ ~ \mathrm{ArcLogisticSequence}_s(T(z))= \mathrm{ArcLogisticSequence}_s(z)+1\) |
| − | Through function ArcLogisticSequence, the elements of the [[logistic sequence]] |
+ | Through function ArcLogisticSequence, the elements of the [[logistic sequence]] \(f\) beginning with \(f_0\) can be expressed through the holomorphic function [[LogisticSequence]]: |
| − | : |
+ | :\(\!\!\!\!\!\!\!\!\!\! (3) ~ ~ ~ f_n=\mathrm{LogisticSequence}_s\Big(n+\mathrm{ArcLogisticSequence}_s(f_0)\Big)\) |
| − | For real values of argument, |
+ | For real values of argument, \(\mathrm{ArcLogisticSequence}_s(x)\) is plotted versus \(x\) for various values of \(s\) in the figure at right. The singularities ([[branchpoint]]s) are marked with black circles. |
| − | For |
+ | For \(s\!=\!3\), the [[complex map]] of \(\mathrm{ArcLogisticSequence}_s\) is shown in figure below. However, with the code supplied, one can plot similar maps for other values of parameter \(s\). |
==Asymptotics== |
==Asymptotics== |
||
| − | : |
+ | : \(\!\!\!\!\!\!\!\!\!\! (4) ~ ~ ~ \displaystyle \mathrm{ArcLogisticSequence}_s=\log_s\left( \sum_{n=1}^{N-1} S_n z^n+ O(z^N)\right)\) |
where |
where |
||
| − | : |
+ | : \(\!\!\!\!\!\!\!\!\!\! (5) ~ ~ ~ S_1=1\) |
| − | : |
+ | : \(\!\!\!\!\!\!\!\!\!\! (6) ~ ~ ~ \displaystyle S_2=\frac{1}{s-1}\) |
| − | : |
+ | : \(\!\!\!\!\!\!\!\!\!\! (7) ~ ~ ~ \displaystyle S_3=\frac{2s}{(s\!-\!1)(s^2\!-\!1)}\) |
| − | The coefficients |
+ | The coefficients \(S\) above can be calculated substituting expansion (4) into the Abel equation (2), or inverting the similar expansion of the [[LogisticSequence]] at large negative values of the argument. |
| − | ==Special case |
+ | ==Special case \(s=4\)== |
| − | For the special case |
+ | For the special case \(s\!=\!4\), \(\mathrm{ArcLogisticSequence}_s\) can be expressed through the elementary function, |
| − | : |
+ | : \(\!\!\!\!\!\!\!\!\!\! (8) ~ ~ ~ \displaystyle \mathrm{ArcLogisticSequence}_4= \log_2\Big(\arccos(1\!-\!2z)\Big)\) |
This case corresponds to the thick pink curve in the figure at the top. |
This case corresponds to the thick pink curve in the figure at the top. |
||
==References== |
==References== |
||
Latest revision as of 18:25, 30 July 2019
ArcLogisticSequence\(_s\) is holomorphic function, inverse of function LogisticSequence, where \(s\) is parameter; usually it is assumed that it has real values. In order to avoid confusions, words Arc, Logistic and Sequence in the name should be written without spacebars: in the common sense and the mathematic notations, the space is usually interpreted as operation of multiplication or combination of functions.
ArcLogisticSequence is Abel function for the Logistic operator as the transfer function,
- \(\!\!\!\!\!\!\!\!\!\! (1) ~ ~ ~ T(z)=\mathrm{LogisticOperator}_s(z)= s\, z\, (1\!-\!z)\)
Tthe ArcLogisticSequence satisfies the Abel equation
- \(\!\!\!\!\!\!\!\!\!\! (2) ~ ~ ~ \mathrm{ArcLogisticSequence}_s(T(z))= \mathrm{ArcLogisticSequence}_s(z)+1\)
Through function ArcLogisticSequence, the elements of the logistic sequence \(f\) beginning with \(f_0\) can be expressed through the holomorphic function LogisticSequence:
- \(\!\!\!\!\!\!\!\!\!\! (3) ~ ~ ~ f_n=\mathrm{LogisticSequence}_s\Big(n+\mathrm{ArcLogisticSequence}_s(f_0)\Big)\)
For real values of argument, \(\mathrm{ArcLogisticSequence}_s(x)\) is plotted versus \(x\) for various values of \(s\) in the figure at right. The singularities (branchpoints) are marked with black circles.
For \(s\!=\!3\), the complex map of \(\mathrm{ArcLogisticSequence}_s\) is shown in figure below. However, with the code supplied, one can plot similar maps for other values of parameter \(s\).
Asymptotics
- \(\!\!\!\!\!\!\!\!\!\! (4) ~ ~ ~ \displaystyle \mathrm{ArcLogisticSequence}_s=\log_s\left( \sum_{n=1}^{N-1} S_n z^n+ O(z^N)\right)\)
where
- \(\!\!\!\!\!\!\!\!\!\! (5) ~ ~ ~ S_1=1\)
- \(\!\!\!\!\!\!\!\!\!\! (6) ~ ~ ~ \displaystyle S_2=\frac{1}{s-1}\)
- \(\!\!\!\!\!\!\!\!\!\! (7) ~ ~ ~ \displaystyle S_3=\frac{2s}{(s\!-\!1)(s^2\!-\!1)}\)
The coefficients \(S\) above can be calculated substituting expansion (4) into the Abel equation (2), or inverting the similar expansion of the LogisticSequence at large negative values of the argument.
Special case \(s=4\)
For the special case \(s\!=\!4\), \(\mathrm{ArcLogisticSequence}_s\) can be expressed through the elementary function,
- \(\!\!\!\!\!\!\!\!\!\! (8) ~ ~ ~ \displaystyle \mathrm{ArcLogisticSequence}_4= \log_2\Big(\arccos(1\!-\!2z)\Big)\)
This case corresponds to the thick pink curve in the figure at the top.
References
http://tori.ils.uec.ac.jp/PAPERS/2010logistie.pdf D.Kouznetsov. Holomorphic extension of the logistic sequence. Moscow University Physics Bulletin, 2010, No.2, p.91-98. (Russian version: p.24-31)
Keywords
LogisticSequence, LogisticOperator, Abel function, Superfunction