Difference between revisions of "BesselK0"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| Line 1: | Line 1: | ||
| − | [[File:Besselk0mapT900.png|right|400px|thumb| |
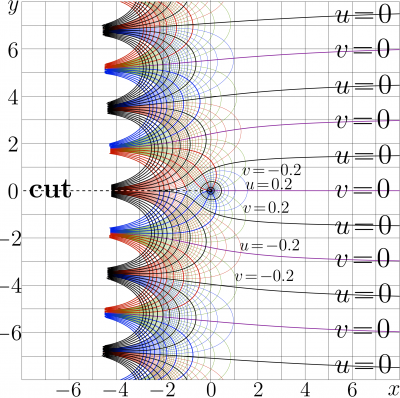
+ | [[File:Besselk0mapT900.png|right|400px|thumb|\(u+\mathrm i v=\mathrm{BesselK0}(x+\mathrm i y)\)]] |
| − | [[File:Besselk0plotT400.png|right|300px|thumb| |
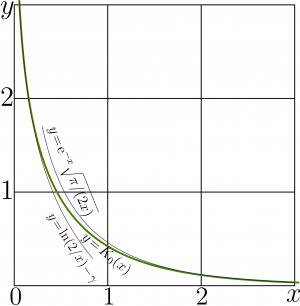
+ | [[File:Besselk0plotT400.png|right|300px|thumb|\(y=\mathrm{BesselK0}(x)\) and two asymptotics]] |
| − | '''BesselK0''' or |
+ | '''BesselK0''' or \(K_0\) is holomorphic function, solution \(f\) of equation |
| − | : |
+ | : \( \!\!\!\!\!\!\!\!\!\!\ (1) ~ ~ ~ \displaystyle |
f''(z)+f(z)/z=f(z) |
f''(z)+f(z)/z=f(z) |
||
| + | \) |
||
| − | $ |
||
that has asymptotic |
that has asymptotic |
||
| − | : |
+ | : \( \!\!\!\!\!\!\!\!\!\!\ (2) ~ ~ ~ \displaystyle |
K_0(z) = \exp(-z)\sqrt{\frac{\pi}{2z}} ~ \Big( 1+ O(1/z)\Big) |
K_0(z) = \exp(-z)\sqrt{\frac{\pi}{2z}} ~ \Big( 1+ O(1/z)\Big) |
||
| + | \) |
||
| − | $ |
||
| − | at large values of |
+ | at large values of \(\Re(z)\). |
| − | The same equation (1) holds also for |
+ | The same equation (1) holds also for \(f(z)=\mathrm{BesselY0}(\mathrm i z)\), where [[BesselY0]] is [[Neumann function]]. |
| − | [[Complex map]] of |
+ | [[Complex map]] of \(f=\mathrm{BesselK0}(x+\mathrm i y)\) is shown in upper figure with |
| − | lines |
+ | lines \(u\!=\!\Re(f)\!=\!\rm const\) and |
| − | lines |
+ | lines \(v\!=\!\Im(f)\!=\!\rm const\) |
| − | in the |
+ | in the \(x\),\(y\) plane. |
==Integral representation== |
==Integral representation== |
||
| − | : |
+ | : \( \!\!\!\!\!\!\!\!\!\!\ (o) ~ ~ ~ \displaystyle |
K_0(z) = \int_0^\infty \exp\!\Big( |
K_0(z) = \int_0^\infty \exp\!\Big( |
||
-z \cosh(t) |
-z \cosh(t) |
||
\Big) ~ \mathrm d t |
\Big) ~ \mathrm d t |
||
| + | \) |
||
| − | $ |
||
==Relation to other [[cylindric function]]s== |
==Relation to other [[cylindric function]]s== |
||
| − | : |
+ | : \( \!\!\!\!\!\!\!\!\!\!\ (o) ~ ~ ~ \displaystyle |
K_0(z)=\frac{\mathrm i \pi}{2} H_0(\mathrm i z) |
K_0(z)=\frac{\mathrm i \pi}{2} H_0(\mathrm i z) |
||
| + | \) |
||
| − | $ |
||
| − | where |
+ | where \(H_0\) is the [[Hankel function]] of zero order, id est, [[BeesselH0]]. |
==Behavior along the real axis== |
==Behavior along the real axis== |
||
| − | Esplicit plot of BesselK0 is shown in figure at right, |
+ | Esplicit plot of BesselK0 is shown in figure at right, \(y=\mathrm{BesselK0}(x)=K_0(x)\). |
For comparison, the two asymptotics are shown, |
For comparison, the two asymptotics are shown, |
||
| − | : |
+ | : \( \!\!\!\!\!\!\!\!\!\!\ (\mathrm A1) ~ ~ ~ \displaystyle y= \exp(-z)\sqrt{\frac{\pi}{2z}} ~ ~ ~ \) and |
| − | : |
+ | : \( \!\!\!\!\!\!\!\!\!\!\ (\mathrm A2) ~ ~ ~ \displaystyle y= \ln \frac{\pi}{2 x} - \mathrm{EulerGamma} ~ ~ ~ \) |
Here [[EulerGamma]] is the Euler constant, |
Here [[EulerGamma]] is the Euler constant, |
||
| − | : |
+ | : \( \!\!\!\!\!\!\!\!\!\!\ (4) ~ ~ ~ \displaystyle |
\mathrm{EulerGamma}=\lim_{n \rightarrow \infty} \left( \sum_{k=1}^{n} \frac{1}{k} - \ln(n) \right) \approx |
\mathrm{EulerGamma}=\lim_{n \rightarrow \infty} \left( \sum_{k=1}^{n} \frac{1}{k} - \ln(n) \right) \approx |
||
0.577215664901532861 |
0.577215664901532861 |
||
| + | \) |
||
| − | $ |
||
The first of them approximates the function at large values of the argument, and the second does for the small values of the argument. |
The first of them approximates the function at large values of the argument, and the second does for the small values of the argument. |
||
| Line 45: | Line 45: | ||
At small values of the argument, BesselK0 expands as follows: |
At small values of the argument, BesselK0 expands as follows: |
||
| − | : |
+ | : \( \!\!\!\!\!\!\!\!\!\!\ (5) ~ ~ ~ \displaystyle |
K_0(z) = \ln(2/z) - \mathrm{EulerGamma} |
K_0(z) = \ln(2/z) - \mathrm{EulerGamma} |
||
+ |
+ |
||
\frac{1}{4}\left( \ln(2/z) + 1 - \mathrm{EulerGamma} \right)~ z^2 + ... |
\frac{1}{4}\left( \ln(2/z) + 1 - \mathrm{EulerGamma} \right)~ z^2 + ... |
||
\frac{1}{128}\left( \ln(2/z) + 3 - 2\mathrm{EulerGamma} \right)~ z^4 + ... |
\frac{1}{128}\left( \ln(2/z) + 3 - 2\mathrm{EulerGamma} \right)~ z^4 + ... |
||
| + | \) |
||
| − | $ |
||
At large values of the argument BesselK0 expands as follows: |
At large values of the argument BesselK0 expands as follows: |
||
| − | : |
+ | : \( \!\!\!\!\!\!\!\!\!\!\ (6) ~ ~ ~ \displaystyle |
K_0(z) = \exp(-z) \sqrt{\frac{\pi}{2z}} \left( |
K_0(z) = \exp(-z) \sqrt{\frac{\pi}{2z}} \left( |
||
1-\frac{1}{8z} |
1-\frac{1}{8z} |
||
+\frac{9}{128 z^2} |
+\frac{9}{128 z^2} |
||
| − | -\frac{75}{1024 z^3}+ .. \right) |
+ | -\frac{75}{1024 z^3}+ .. \right)\) |
The [[Mathematica]] easy calculates some tens of terms in the expansions above. |
The [[Mathematica]] easy calculates some tens of terms in the expansions above. |
||
The leading terms of these expansions are shown in the explicit plot at right. |
The leading terms of these expansions are shown in the explicit plot at right. |
||
Latest revision as of 18:26, 30 July 2019
BesselK0 or \(K_0\) is holomorphic function, solution \(f\) of equation
- \( \!\!\!\!\!\!\!\!\!\!\ (1) ~ ~ ~ \displaystyle f''(z)+f(z)/z=f(z) \)
that has asymptotic
- \( \!\!\!\!\!\!\!\!\!\!\ (2) ~ ~ ~ \displaystyle K_0(z) = \exp(-z)\sqrt{\frac{\pi}{2z}} ~ \Big( 1+ O(1/z)\Big) \)
at large values of \(\Re(z)\). The same equation (1) holds also for \(f(z)=\mathrm{BesselY0}(\mathrm i z)\), where BesselY0 is Neumann function.
Complex map of \(f=\mathrm{BesselK0}(x+\mathrm i y)\) is shown in upper figure with lines \(u\!=\!\Re(f)\!=\!\rm const\) and lines \(v\!=\!\Im(f)\!=\!\rm const\) in the \(x\),\(y\) plane.
Integral representation
- \( \!\!\!\!\!\!\!\!\!\!\ (o) ~ ~ ~ \displaystyle K_0(z) = \int_0^\infty \exp\!\Big( -z \cosh(t) \Big) ~ \mathrm d t \)
Relation to other cylindric functions
- \( \!\!\!\!\!\!\!\!\!\!\ (o) ~ ~ ~ \displaystyle K_0(z)=\frac{\mathrm i \pi}{2} H_0(\mathrm i z) \)
where \(H_0\) is the Hankel function of zero order, id est, BeesselH0.
Behavior along the real axis
Esplicit plot of BesselK0 is shown in figure at right, \(y=\mathrm{BesselK0}(x)=K_0(x)\). For comparison, the two asymptotics are shown,
- \( \!\!\!\!\!\!\!\!\!\!\ (\mathrm A1) ~ ~ ~ \displaystyle y= \exp(-z)\sqrt{\frac{\pi}{2z}} ~ ~ ~ \) and
- \( \!\!\!\!\!\!\!\!\!\!\ (\mathrm A2) ~ ~ ~ \displaystyle y= \ln \frac{\pi}{2 x} - \mathrm{EulerGamma} ~ ~ ~ \)
Here EulerGamma is the Euler constant,
- \( \!\!\!\!\!\!\!\!\!\!\ (4) ~ ~ ~ \displaystyle \mathrm{EulerGamma}=\lim_{n \rightarrow \infty} \left( \sum_{k=1}^{n} \frac{1}{k} - \ln(n) \right) \approx 0.577215664901532861 \)
The first of them approximates the function at large values of the argument, and the second does for the small values of the argument.
Expansions
At small values of the argument, BesselK0 expands as follows:
- \( \!\!\!\!\!\!\!\!\!\!\ (5) ~ ~ ~ \displaystyle K_0(z) = \ln(2/z) - \mathrm{EulerGamma} + \frac{1}{4}\left( \ln(2/z) + 1 - \mathrm{EulerGamma} \right)~ z^2 + ... \frac{1}{128}\left( \ln(2/z) + 3 - 2\mathrm{EulerGamma} \right)~ z^4 + ... \)
At large values of the argument BesselK0 expands as follows:
- \( \!\!\!\!\!\!\!\!\!\!\ (6) ~ ~ ~ \displaystyle K_0(z) = \exp(-z) \sqrt{\frac{\pi}{2z}} \left( 1-\frac{1}{8z} +\frac{9}{128 z^2} -\frac{75}{1024 z^3}+ .. \right)\)
The Mathematica easy calculates some tens of terms in the expansions above. The leading terms of these expansions are shown in the explicit plot at right. These expansions are used in the numerical implementation.
References
http://mathworld.wolfram.com/BesselFunctionoftheSecondKind.html