Difference between revisions of "StraRo"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| Line 1: | Line 1: | ||
| − | [[File:Straroplot.jpg|300px|thumb|Fig.1. |
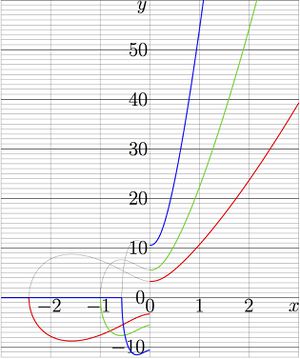
+ | [[File:Straroplot.jpg|300px|thumb|Fig.1. \(y=\mathrm{StraRo}_q(x)\) for \(q\!=\!0.5\) , red, for |
| − | + | \(q\!=\!1\) , green, and for \(q\!=\!2\) , blue]] |
|
| − | [[File:Straro05at.jpg|300px|thumb|Fig.2. |
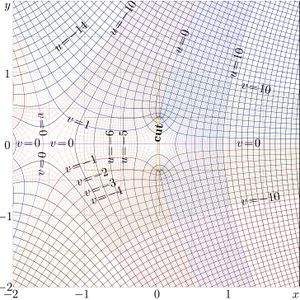
+ | [[File:Straro05at.jpg|300px|thumb|Fig.2. \(u\!+\!\mathrm i v=\mathrm{StraRo}_{0.5}(x\!+\!\mathrm i y\)]] |
| − | [[File:Straro10at.jpg|300px|thumb|Fig.3. |
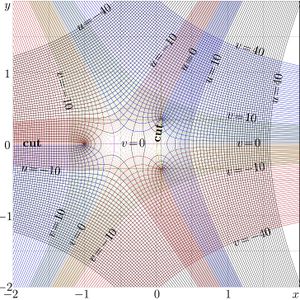
+ | [[File:Straro10at.jpg|300px|thumb|Fig.3. \(u\!+\!\mathrm i v=\mathrm{StraRo}_{1}(x\!+\!\mathrm i y\)]] |
| − | [[File:Straro20at.jpg|300px|thumb|Fig.4. |
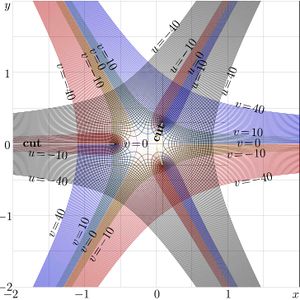
+ | [[File:Straro20at.jpg|300px|thumb|Fig.4. \(u\!+\!\mathrm i v=\mathrm{StraRo}_{2}(x\!+\!\mathrm i y\)]] |
[[StraRo]], or [[Strange root]] is function that happened to be useful for evaluation of function [[ArqNem]], that, it its turn, is necessary for evaluation of the [[Abel function]] of the [[Nemtsov Function]]. |
[[StraRo]], or [[Strange root]] is function that happened to be useful for evaluation of function [[ArqNem]], that, it its turn, is necessary for evaluation of the [[Abel function]] of the [[Nemtsov Function]]. |
||
| − | StraRo has singe parameter, denoted gere with letter |
+ | StraRo has singe parameter, denoted gere with letter \(q\). |
==Description== |
==Description== |
||
Let |
Let |
||
| − | + | \(\mathrm{StraR}_q(z)=\sqrt{27 (q\! -\! z)^2 + 4 (1\!+\! 4 q z)^3} \) |
|
<!-- = \sqrt{4 + 27 q^2 - 6 q z + 27 z^2 + 192 q^2 z^2 + 256 q^3 z^3} !--> |
<!-- = \sqrt{4 + 27 q^2 - 6 q z + 27 z^2 + 192 q^2 z^2 + 256 q^3 z^3} !--> |
||
In vicinity of the positive part of the real axis, |
In vicinity of the positive part of the real axis, |
||
| − | + | \(\mathrm{StraRo}_q\) coincides with \(\mathrm{StraR}_q\) . |
|
| − | For |
+ | For \(q\!=\!0.5\), \(q\!=\!1\) and \(q\!=\!2\), for real values of the argument, function \(\mathrm{StraR}_q(x)\) is shown in figure at right with thin curves, \(y=\mathrm{StraR}_q(x)\). |
| − | The thick curves show |
+ | The thick curves show \(y=\mathrm{StraRo}_q(x)\), and for positive \(x\), the thin and thick curves overlap. |
| − | Function StraR is not so good for construction of function |
+ | Function StraR is not so good for construction of function \(\mathrm{ArqNem}_q=\mathrm{Nem}_q^{-1}\), |
because StraR has cut lines, that limit the range of holomorphizm. |
because StraR has cut lines, that limit the range of holomorphizm. |
||
Funiction StraR has cut lines along the negative part of the real axis, and also two segments from zero to the brachpoints |
Funiction StraR has cut lines along the negative part of the real axis, and also two segments from zero to the brachpoints |
||
| − | + | \(\mathrm{NemBra}(q)\) and \(\mathrm{NemBra}(q)^*\). There is special article about function [[NemBra]]. |
|
| − | For |
+ | For \(q\!=\!0.5\), \(q\!=\!1\) and \(q\!=\!2\), the complex maps of function \(\mathrm{StraR}_q\) are shown in figures 2,3,4: |
| − | + | \(u\!+\!\mathrm i v=\mathrm{StraRo}_q(x\!+\!\mathrm i y)\) |
|
==Explicit representation== |
==Explicit representation== |
||
| − | Let |
+ | Let \(Q\) and \(S\) be global variables that store values of \(q\) and \(\mathrm{NemBra}(q)\) |
| − | Then, evaluation of |
+ | Then, evaluation of \(\mathrm{StraRo}_q(z)\) for complex \(z\) can be performed with the short code below: |
<poem><nomathjax><nowiki> |
<poem><nomathjax><nowiki> |
||
z_type F(z_type z){ z_type a,b,r,R ; a=Q-z; b=1. + 4.*Q*z; r = 27.*a*a + 4.*b*b*b ; |
z_type F(z_type z){ z_type a,b,r,R ; a=Q-z; b=1. + 4.*Q*z; r = 27.*a*a + 4.*b*b*b ; |
||
| Line 49: | Line 49: | ||
==Usage== |
==Usage== |
||
| − | Function [[StraRo]] appears at the inversion of the [[Nemtsov function]] |
+ | Function [[StraRo]] appears at the inversion of the [[Nemtsov function]] \(T\). |
| − | Let |
+ | Let \(T(z)=\mathrm{Nem}_q(z)=T[z_] = z + z^3 + q z^4\) |
Then, the inversion can be performed with Mathematica command |
Then, the inversion can be performed with Mathematica command |
||
| Line 70: | Line 70: | ||
</nomathjax> |
</nomathjax> |
||
| − | does |
+ | does \(1/27 (729 (q - z)^2 + 108 (1 + 4 q z)^3)\) |
| − | instead of expected |
+ | instead of expected \(27 (q - z)^2 + 4 (1 + 4 q z)^3\) |
However, the simplified expression can be obtained at Mathematica with the manual trick, that bypasses the bug mentioned: |
However, the simplified expression can be obtained at Mathematica with the manual trick, that bypasses the bug mentioned: |
||
| Line 80: | Line 80: | ||
</nomathjax> |
</nomathjax> |
||
| − | that gives expression |
+ | that gives expression \(27 (q - z)^2 + 4 (1 + 4 q z)^3\) |
| − | One of holomorphic extensions of the square root of this expression is denined as [[StraRo]], and the corresponding value of parameter |
+ | One of holomorphic extensions of the square root of this expression is denined as [[StraRo]], and the corresponding value of parameter \(q\) is indicates as subscript. |
The special, and may be, a little bis strange position of the cut lines of function [[StraRo]] is used as a pretext call this function "strange root", and shortening of "strange root" gives the name of the function [[StraRo]]. |
The special, and may be, a little bis strange position of the cut lines of function [[StraRo]] is used as a pretext call this function "strange root", and shortening of "strange root" gives the name of the function [[StraRo]]. |
||
Latest revision as of 18:47, 30 July 2019
StraRo, or Strange root is function that happened to be useful for evaluation of function ArqNem, that, it its turn, is necessary for evaluation of the Abel function of the Nemtsov Function.
StraRo has singe parameter, denoted gere with letter \(q\).
Description
Let
\(\mathrm{StraR}_q(z)=\sqrt{27 (q\! -\! z)^2 + 4 (1\!+\! 4 q z)^3} \)
In vicinity of the positive part of the real axis,
\(\mathrm{StraRo}_q\) coincides with \(\mathrm{StraR}_q\) .
For \(q\!=\!0.5\), \(q\!=\!1\) and \(q\!=\!2\), for real values of the argument, function \(\mathrm{StraR}_q(x)\) is shown in figure at right with thin curves, \(y=\mathrm{StraR}_q(x)\). The thick curves show \(y=\mathrm{StraRo}_q(x)\), and for positive \(x\), the thin and thick curves overlap.
Function StraR is not so good for construction of function \(\mathrm{ArqNem}_q=\mathrm{Nem}_q^{-1}\), because StraR has cut lines, that limit the range of holomorphizm.
Funiction StraR has cut lines along the negative part of the real axis, and also two segments from zero to the brachpoints \(\mathrm{NemBra}(q)\) and \(\mathrm{NemBra}(q)^*\). There is special article about function NemBra.
For \(q\!=\!0.5\), \(q\!=\!1\) and \(q\!=\!2\), the complex maps of function \(\mathrm{StraR}_q\) are shown in figures 2,3,4:
\(u\!+\!\mathrm i v=\mathrm{StraRo}_q(x\!+\!\mathrm i y)\)
Explicit representation
Let \(Q\) and \(S\) be global variables that store values of \(q\) and \(\mathrm{NemBra}(q)\)
Then, evaluation of \(\mathrm{StraRo}_q(z)\) for complex \(z\) can be performed with the short code below:
z_type F(z_type z){ z_type a,b,r,R ; a=Q-z; b=1. + 4.*Q*z; r = 27.*a*a + 4.*b*b*b ;
DB x,y; x=Re(z); y=Im(z);
if( x<=0 ) return -sqrt(r);
if( y > Im(S) ) return I*sqrt(-r);
if( y < - Im(S) ) return -I*sqrt(-r);
if( x*Im(S)< fabs(y)*Re(S) ) return -sqrt(r);
return sqrt(r);
}
Usage
Function StraRo appears at the inversion of the Nemtsov function \(T\).
Let \(T(z)=\mathrm{Nem}_q(z)=T[z_] = z + z^3 + q z^4\)
Then, the inversion can be performed with Mathematica command
so = Solve[T[A] == z, A]
The Second solution can be extracted with
so2 = ReplaceAll[A, Extract[so, 2]]
The resulting expression has combination (27 q - 27 z)^2 - 4 (-3 - 12 q z)^3, namely, square root of this expression.
Unfortunately, Mathematica does not extract factor 27 from this expression automatically.
FullSimplify[(27 q - 27 z)^2/27 - 4 (-3 - 12 q z)^3/27]
does \(1/27 (729 (q - z)^2 + 108 (1 + 4 q z)^3)\)
instead of expected \(27 (q - z)^2 + 4 (1 + 4 q z)^3\)
However, the simplified expression can be obtained at Mathematica with the manual trick, that bypasses the bug mentioned:
FullSimplify[(27 q - 27 z)^2/27] - 4 FullSimplify[(-3 - 12 q z)^3/27]
that gives expression \(27 (q - z)^2 + 4 (1 + 4 q z)^3\)
One of holomorphic extensions of the square root of this expression is denined as StraRo, and the corresponding value of parameter \(q\) is indicates as subscript. The special, and may be, a little bis strange position of the cut lines of function StraRo is used as a pretext call this function "strange root", and shortening of "strange root" gives the name of the function StraRo.
References
Keywords
Abel function, ArqNem, AuNem, Book, Mathematica, Nemtsov function, Superfunction, Superfunctions