Difference between revisions of "Theorem on increment of tetration"
m (T moved page Theorem on increment of superfunctions to Theorem on increment of tetration) |
|||
| Line 1: | Line 1: | ||
| − | [[Theorem on increment of |
+ | [[Theorem on increment of tetration]] is statement about asymptotic behavior of solution of the [[Transfer equation]] with exponential transfer functions. It applies not only to [[tetration]], but also to other superexponentials. |
==Statement== |
==Statement== |
||
| Line 22: | Line 22: | ||
\( \Im(K) = \Im(k) \) |
\( \Im(K) = \Im(k) \) |
||
| + | ==Applications== |
||
| + | <div style="float:right;width:300px"> |
||
| + | <div style="width:320px"> |
||
| + | [[File:TetKK200.png|320px]]<small> |
||
| + | Fig.1. Asymptoric parameters of [[Tetration]] versus \(\beta\) |
||
| + | </small> |
||
| + | </div></div> |
||
| + | Fig.1 shows the asymptotic parameters of [[tetration]] to base \(\ln(\beta)\): |
||
| + | Real and imaginary parts of the [[fixed point]]s |
||
| ⚫ | |||
| ⚫ | |||
| + | \(L=L_1=\) [[Filog]]\((\beta)\) |
||
| − | ==Keywords== |
||
| − | [[Fixed point]], |
||
| − | [[Kneser expansion]], |
||
| − | [[Superfunction]], |
||
| − | [[Tetration]] |
||
| + | and |
||
| ⚫ | |||
| + | |||
| − | [[Category:Kneser expansion]] |
||
| + | \(L=L_1=\) [[Filog]]\((\beta^*)^*\) |
||
| + | |||
| + | Real and imaginary parts of the asymptotic growing factor |
||
| + | |||
| + | \(K= \beta L\) |
||
| + | |||
| + | Real and imaginary parts of the asymptotic increment |
||
| + | |||
| + | \(k=\ln(K) \) |
||
| + | |||
| + | For \(\beta < 1/\mathrm e\), the two fixed points are shown; |
||
| + | and the two values of the corresponding growing factor and two values of the corresponding increment are drown. |
||
| + | |||
| + | For real positive \(\beta\), |
||
| + | |||
| + | The imaginary parts of \(K\) and \(k\) coincide. |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
[[Category:Superfunction]] |
[[Category:Superfunction]] |
||
[[Category:Tetration]] |
[[Category:Tetration]] |
||
Revision as of 12:53, 12 August 2020
Theorem on increment of tetration is statement about asymptotic behavior of solution of the Transfer equation with exponential transfer functions. It applies not only to tetration, but also to other superexponentials.
Statement
Let \(F\) be solution of equation
\(F(z\!+\!1)=\exp\big(\beta F(z)\big)\)
for some \(\beta>0\).
Let \(L\) be the fixed point, id est, \(\exp(\beta L)=L\)
Let \(F(z)=L+\varepsilon+O(\varepsilon^2) \)
where \(\varepsilon = \exp(kz) \) for some increment \(k\).
Let \(~ K\!=\!\exp(k)\)
Then
\( \Im(K) = \Im(k) \)
Applications
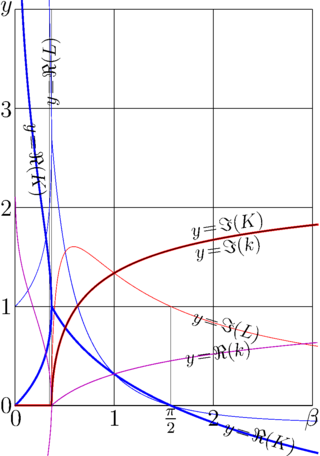 Fig.1. Asymptoric parameters of Tetration versus \(\beta\)
Fig.1. Asymptoric parameters of Tetration versus \(\beta\)
Fig.1 shows the asymptotic parameters of tetration to base \(\ln(\beta)\):
Real and imaginary parts of the fixed points
\(L=L_1=\) Filog\((\beta)\)
and
\(L=L_1=\) Filog\((\beta^*)^*\)
Real and imaginary parts of the asymptotic growing factor
\(K= \beta L\)
Real and imaginary parts of the asymptotic increment
\(k=\ln(K) \)
For \(\beta < 1/\mathrm e\), the two fixed points are shown; and the two values of the corresponding growing factor and two values of the corresponding increment are drown.
For real positive \(\beta\),
The imaginary parts of \(K\) and \(k\) coincide.