Difference between revisions of "Linear fuction"
| Line 1: | Line 1: | ||
| − | [[File:Itelin125T.jpg| |
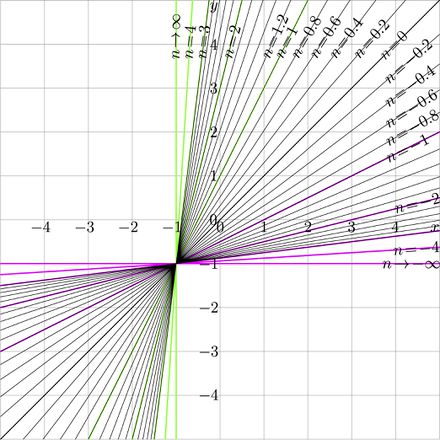
+ | [[File:Itelin125T.jpg|440px|thumb|Iterates of $T(z)=A+Bz~$ at $~A\!=\!1$, $B\!=\!2~$; $~y=T^n(x)~$ versus $x$ for various $n$]] |
[[Linear function]] is function that can be represented in form |
[[Linear function]] is function that can be represented in form |
||
Revision as of 19:10, 18 September 2013
Linear function is function that can be represented in form
$(1) ~ ~ ~ T(z)=A+B z$
where $A$ and $B$ are constants (for example some complex numbers)
Abelfunction and Superfunction
Superfunction $F$ for the linear function $T$ by (1) can be written as follows:
$(2) ~ ~ ~ \displaystyle F(z)= A \frac{1-B^z}{1-B}$
The corresponding Abel function can be expressed as follows:
$(3) ~ ~ ~ \displaystyle G(z)= \log_B\Big(1+\frac{B-1}{A}z \big)$
Iterates
Iterate of the linear function can be expressed through the superfunction and the Abel function in the standard way,
$(4) ~ ~ ~ \displaystyle T^n(z)=F(n+G(z))$
Substitution of the Superfunction $F$ by (2) and the Abel function $G$ by (3) into equation (4) gives aslo linear function
$(5) ~ ~ ~ \displaystyle T^n(z)= \frac{-A+B^n\Big( A+(-1+B) z\Big)}{-1+B}=A \frac {B^n-1}{B-1} +B^n z$
with new parameters $A \frac {B^n-1}{B-1}$ instead of $A$ in (1) and $B^n$ instead of $B$. With this representation, the number $n$ of iteration has no need to be integer. As other holomophic functions, the linear function can be iterated even complex number of times.
References
Keywords
Abel function, Holomorphic function, Iteration, Superfunction