BesselJ0
BesselJ0 called also the Bessel function of zero order and also $J_0$, is entire function, solution of equation
- $ \!\!\!\!\!\!\!\!\!\! (1) \displaystyle ~ ~ ~
J_0(z)+ J_0'(z)/z+ J_0(z)=0 $
- $ \!\!\!\!\!\!\!\!\!\! (2) \displaystyle ~ ~ ~ J_0(0)=1 ~, ~~ J_0'(0)=0$
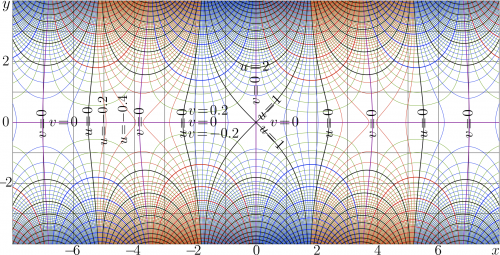
Complex map of function BesselJ0 is shown in figure at right. The short notation $J_0=\mathrm{BesselJ0}$ is also valid.
Integral representation
- $ \!\!\!\!\!\!\!\!\!\! (3) \displaystyle ~ ~ ~ \mathrm{BesselJ}_0(z)=
\frac{1}{\pi}\int_0^\pi \cos\!\big( z \cos (t) \big)~ \mathrm d t $
Symmetry
The BesselJ0 is symmetric function,
- $ \!\!\!\!\!\!\!\!\!\! (4) \displaystyle ~ ~ ~ \mathrm{BesselJ}_0'(0)=1$
In particular,
- $ \!\!\!\!\!\!\!\!\!\! (5) \displaystyle ~ ~ ~ \mathrm{BesselJ}_0(-z)= \mathrm{BesselJ}_0(z)$
Expansion at zero
The straightforward Taylor expansion at zero can be written as follows:
- $ \!\!\!\!\!\!\!\!\!\! (6) \displaystyle ~ ~ ~ \mathrm{BesselJ}_0(z)=
\sum_{n=0}^{\infty} \frac{ (-z^2/4)^n } {\mathrm{Factorial}(n)^2} = 1 -\frac{z^2}{4} +\frac{z^4}{64} -\frac{z^6}{2304}+ ... $
The series converges in the whole complex plane and, at the complex(double) arithmetics, gives of order of dozen significant figures at least for $|z|\!<\!20$; it is sufficient to keep few tens of terms in the expansion. For larger values of the argument, the expansion below can be used.
Expansion at infinity
Expansion at large vales of the argument can be written as follows:
- $ \!\!\!\!\!\!\!\!\!\! (8) \displaystyle ~ ~ ~ J_0(z)=
\sqrt{\frac{2}{\pi z}} \cos\!\left(z-\frac{\pi}{4}\right) \left( 1 - \frac{9}{128 z^2}+ ..\right) + \sqrt{\frac{2}{\pi z}} \sin\!\left(z-\frac{\pi}{4}\right) \frac{1}{8z}\left( 1 - \frac{75}{128 z^2}+ ..\right) $
Mathematica allows to calculate a dozen of term of this expansion; they can be extracted also from the complex(double) implementation Besselj0.cin.
Behavior along the real axis
Along the real axis, BesselJ0 oscillates (like other Bessel functions). The zeros of are denoted with $j_{0,n}$; where $n$ is supposed to be positive integer. The WebMatematica offers the on-line service to evaluate these zeros [1]; a thousand of zeros can be evaluated within few seconds. In particular, the first 5 values are
- 2.404825557695773
- 5.520078110286311
- 8.653727912911011
- 11.79153443901428
- 14.93091770848779
Integral properties
The orthogonality properties for the zero-th Bessel is suggested [2] in the following form:
- $ \displaystyle \int_0^W ~ J_0(s_p r)~ j_0(s_q r) ~r~ \mathrm d r = \delta_{p,q} \frac{W^2}{2} J_0'(s_p W)^2$
- $ \displaystyle \int_0^W ~ J_0(s r_q)~ j_0(s r_p) ~r~ \mathrm d r = \delta_{p,q} \frac{S^2}{2} J_0'(S\, r_p )^2$
- $ r_{2n+1}=W ~ ~ , ~ ~ s_{n+1}=S$
- $ \zeta_{2n+1}=SW$
That needs to be somehow interpreted.
Numerical implementation
Application
The Bessel function appear at the consideration of wave equations with circular symmetry.
References
- ↑ http://cose.math.bas.bg/webMathematica/webComputing/BesselZeros.jsp
- ↑ http://www.scribd.com/doc/62046269/29/A-5-Bessel-Transform-and-Discrete-Bessel-Transform ANALYSIS AND DESIGN OF VERTICAL CAVITY SURFACE EMITTING LASERS. WILEY SERIES IN LASERS AND APPLICATIONS. D. R. VIJ, Editor, Kurukshetra University. S.F.Yu. School of Electrical & Electronic Engineering, Nanyang Technological University.Singapore.