SuPow

Fig.1. Quadratic function (black curve) and two its superfunctions

Fig.2. $u\!+\!\mathrm i v \!=\! \mathrm{SuPow}_2(x\!+\!\mathrm i y)$

SuPow is specific superpower function, id est, the superfunction of the power function $~z\mapsto z^a\!=\!\exp(\ln(z) \,a)~$

For given parameter $a$,

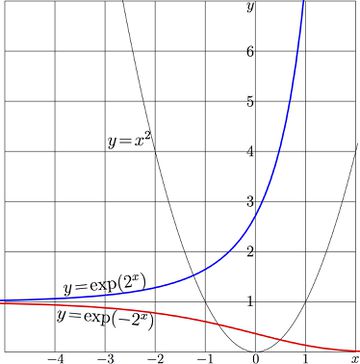
$\mathrm{SuPow}_a(z)=\exp(a^z)$

Usually, it is assumed, that $a\!>\!1$.

Transfer function

Function $F\!=\!\mathrm{SuPow}_a$ is superfunction for the specific power function $T(z)\!=\!z^a$. The superfunction satisfies the transfer equation

$T(F(z))=F(z\!+\!1)$

another solution is denoted as SdPow;

$\mathrm{SdPow}_a(z)=\exp(-a^z)$

For $a\!=\!2$ graphics $y=T(x)$, $y=\mathrm{SuPow}_2(x)$ and $y=\mathrm{SdPow}_2(x)$ are shown in Fig.1.

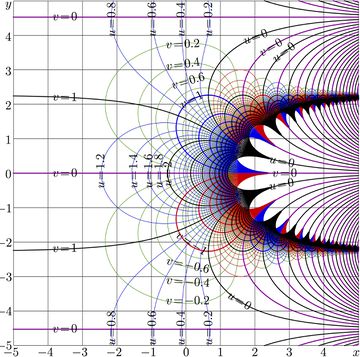
For $a\!=\!2$, complex map of function $\mathrm{SuPow}_a$ is shown in Fig.2.

SuPow and SdPow

Function $\mathrm{SuPow}_a$ is periodic, as well as function $\mathrm{SdPow}_a$

The period $P=2\pi\mathrm i / \ln(a)$ is the same for both these functions.

For $a\!>\!1$, the period is pure imaginary. A little bit more than one period fits the range of map in Fig.2.

Such a periodicity is typical for a superfunction of a transfer function with a real fixed point. Some of thiese function are listed in the Table of superfunctions.

Functions SuPow and SdPow are related with expression

$\mathrm{SuPow}_a(z)=\mathrm{SdPow}_a(z\!+\!P/2)$

Similar relations hold also for many other pairs of periodic superfunctions of some transfer function with two fixed points

However, namely the superpower functions have also the specific relation,

$\displaystyle \mathrm{SuPow}_a(z)=\frac{1}{\mathrm{SdPow}_a(z)}$

Inverse function

$u\!+\!\mathrm i v=\mathrm{AuPow}_2(x\!+\!\mathrm i y)$

The inverse function AuPow$=\mathrm{SuPow}^{-1}$ is also elementary function;

$\mathrm{AuPow}_a(z)=\log_a(\ln(z))$

AuPow is the Abel function for the same transfer function $T(z)=z^a$ and satisfies the Abel equation

$\mathrm{AuPow}_a(z^a)=\mathrm{AuPow}_a(z)+1$

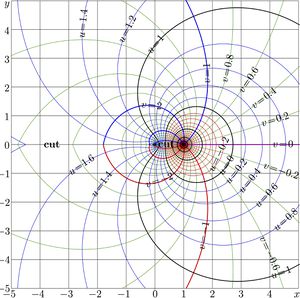
Complex map of function $\mathrm{AuPow}_2$ is shown in figure at right.

For $a\!>\!1$, function $\mathrm{AuPow}_2$ has cut line along the real axis from $1$ to $-\infty$.

Keywords

AuPow, Book, Power function, SdPow, Superfunction, Superfunctions, Superpower