AdPow

Fig.1. $y\!=\!\mathrm{AdPow}_2(x)$ and $y\!=\!\mathrm{AuPow}_2(x)$

Fig.2. $u\!+\!\mathrm i v\!=\!\mathrm{AdPow}_2(x\!+\!\mathrm i y)$

AdPow is specific Abelpower function, id est, the specific Abel function for the Power function.

AdPow can be expressed as elementary function,

$\mathrm{AdPow}_a(z)=\log_a(\ln(1/z))$

Where $a$ is parameter. Usually, it is assumed that $a\!>\!0$.

AdPow is inverse function of SdPow, that, in its turn, is superfunction of the power function.

AdPow and AuPow

Another abelfunction for the power function is called AuPow;

$\mathrm{AdPow}_a(z)=\log_a(\ln(z))$

AdPow is related with AuPow function with simple relation:

$\mathrm{AdPow}_a(z)=\mathrm{AuPow}_a(1/z)$

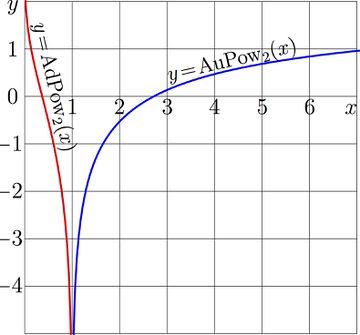
For $a\!=\!2$, both functions AdPow and AuPow are shown in Fig.1

For the same $a\!=\!2$, complex map of function AdPow is shown in Fig.2.

Inverse function

For AdPow, the inverse function is SdPow, that is superpower function, id est, superfunction of the power function:

$\mathrm{AdPow}_a=\mathrm{SdPow}_a^{-1}$

SdPow satisfies the Transfer equation

$\mathrm{SdPow}_a(z\!+\!1)=\mathrm{SdPow}_a(z)^a$

SdPow is elementary function,

$\mathrm{SdPow}_a(z)= \exp(-a^z)$

Applications

AdPow appears as example of the Abel function that can be expressed as elementary function. This allows to trace evaluation of superfunction through the regular iteration; the fixed point unity can be used for the calculation.

Keywords

Abel function AdPow Abel function Elementary function Power function SdPow Superfunctions SdPow Superfunctions