SdPow
SdPow is specific superpower function, id est, the superfunction of the power function $~z\mapsto z^a\!=\!\exp(\ln(z) \,a)~$
For given parameter $a$,
$\mathrm{SdPow}_a(z)=\exp(a^z)$
Usually, it is assumed, that $a\!>\!1$.
Transfer function
Function $F\!=\!\mathrm{SdPow}_a$ is superfunction for the specific power function $T(z)\!=\!z^a$. The superfunction satisfies the transfer equation
$T(F(z))=F(z\!+\!1)$
For this specific transfer function $T$, the two real-holomorphix solutions are SuPow and SdPow:
$\mathrm{SdPow}_a(z)=\exp(-a^z)$
$\mathrm{SuPow}_a(z)=\exp(a^z)$
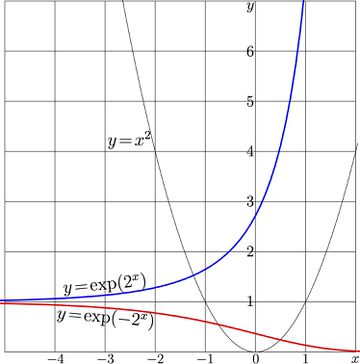
For the power function both, the superfunctions and the Abel functions can be expressed as elementary functions. For $a\!=\!2$, these functions are who functions are shown in Fig.1.
For the same $a\!=\!2$, the complex map of function SdPow is shown in FIg.2.
References
Keywords
AdPow, Elementary function, Power function, SdPow, SuPow, Superfunction Superpower
