Search results

Create the page "Plots of functions" on this wiki! See also the search results found.

• Tetration
  is the \(\mathbb C \mapsto \mathbb C\) function, which is solution of equations ...n]] of [[exponential]] to base \(b\). Exponential is [[transfer function]] of tetration.
  21 KB (3,175 words) - 23:37, 2 May 2021
• Superfunction
  [[Superfunction]] comes from iteration of some function. ...derbrace{T\Big(T\big(... T(t)...\big)\Big)}} \atop {z \mathrm{~evaluations~of~function~}T\!
  25 KB (3,622 words) - 08:35, 3 May 2021
• Regular Iteration
  A [[fractional iterate]] $\phi$ of an analytic function $f$ at fixpoint $a$ is called regular, iff $\phi$ is a ...rtrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.
  20 KB (3,010 words) - 18:11, 11 June 2022
• SuperFactorial
  '''SuperFactorial''', or "superfactorial" is [[superfunction]] of [[factorial]] constructed at its [[fixed point]] 2. Here, the upper index of a function indicates the number of [[iteration]]s.
  18 KB (2,278 words) - 00:03, 29 February 2024
• Complex map
  ...of a [[holomorphic function]] with the isolines of its real part and those of its imaginary part. ...ction, in any point, the isolines of the real part are orthogonal to those of the imaginary part; therefore the the complex maps have specific mesh-like
  2 KB (254 words) - 06:59, 1 December 2018
• Mathematica
  ...upports this language, developed by the [[Wolfram corporation]] in the end of century 20 for simplification of mathematical expressions, solving equations, evaluation of functions, plotting graphics and other things that require some [[mathematics]].
  12 KB (1,901 words) - 18:43, 30 July 2019
• LogisticSequence
  specific [[superfunction]] of the special case of quadratic [[transfer function]] called [[Logistic]] function or [[LogisticO ...ticSequence are shown in two figures at right. Below, the [[complex map]]s of function \(\mathrm{LogisticSequence}_s\) are shown for \(s\!=\!3\) and for
  7 KB (886 words) - 18:26, 30 July 2019
• Logistic operator
  [[File:Logi1a345T300.png|600px|thumb|<small> Various iterates of \(T^c=\mathrm{LogisticOperator}_s\) for D.Kouznetsov. Holomorphic extension of the logistic sequence. Moscow University Physics Bulletin, 2010, No.2, p.91
  6 KB (817 words) - 19:54, 5 August 2020
• ArcLambertW
  One of the inverse function of [[ArcLambertW]] is called [[LambertW]] In wide ranges of values of \(z\), the relations
  3 KB (499 words) - 18:25, 30 July 2019
• Power function
  [[Power function]] ([[Степенная функция]]) is one of the primary [[elementary function]]s; ...eal plot of function \(T(z)\!=\!z^a\) is shown in Fig.1 for several values of \(a\).
  15 KB (2,495 words) - 18:43, 30 July 2019
• C++
  ...] is [[programming language]] characterized with simple syntax, efficiency of compilers and the resulting executable files. C++ is extension of the previously developed language '''C''', that allows to deal with [[compl
  4 KB (608 words) - 15:01, 20 June 2013

• File:Factorialz.jpg the lines of constant <math>u=\Re(z!)</math> and the lines of constant <math>v=\Im(z!)</math> are shown. (1,219 × 927 (479 KB)) - 08:35, 1 December 2018

• File:FactoReal.jpg Factorial of the real argument. Copy from Graphic of [[factorial]]<math>(x)=x!</math> versus real <math>x</math>, red; (915 × 1,310 (141 KB)) - 08:35, 1 December 2018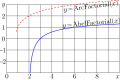

• File:AbelFactorialR.png [[Arcfactorial]] is inverse function of [[Factorial]] [[AbelFactorial]] is inverse function of [[SuperFactorial]], <br> (1,060 × 705 (34 KB)) - 09:39, 21 June 2013

• File:AsincplotT500.png Explicit plot of functions [[ArcSinc]] (thick blue curve) and [[ArcCosc]] (thin red curve): For comparison, the two asymptotics of function ArcSinc are also plotted with thin black curves: (843 × 2,014 (184 KB)) - 09:41, 21 June 2013

• File:Logi1a345T300.png ...]]s of various iterations of the [[Logistic operator]] with various values of parameter $s$. ...on-integer iterates of the [[logisticOperator]] are calculated through the functions [[LogisticSequence]] and [[ArcLogisticSequence]] with (1,636 × 565 (184 KB)) - 08:41, 1 December 2018

• File:SquareRootOfFactorial.png Graphical representation of the [[Square root of factorial]]: functions<br> [[Category:Explicit plots]] (538 × 1,050 (34 KB)) - 09:39, 21 June 2013

• File:Superfactorea500.png Real-real plot of [[SuperFactorial]] is [[superfunction]] of Factorial constructed with [[regular iteration]] at its fixed point 2; (575 × 748 (50 KB)) - 00:06, 29 February 2024

• File:TaniaPlot.png Explicit plot of the [[Tania function]], $y=\mathrm{Tania}(x)$. $f=\mathrm{Tania}$ is solution of the equaitons (807 × 424 (16 KB)) - 09:39, 21 June 2013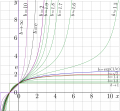

• File:Tetreal10bx10d.png Plot of [[Tetration]]: $y=\mathrm{tet}_b(x)$ versus $x$ for the errors of the fitting are not seen even at the zooming-in. (2,192 × 2,026 (436 KB)) - 13:56, 5 August 2020

View (previous 20 | next 20) (20 | 50 | 100 | 250 | 500)