Search results
Create the page "Asymptotic series" on this wiki! See also the search results found.
File:DSC01693bangkokA.JPG ...cients with $\varepsilon^3$, and so on, getting the asymptotic series. The series gives the good approximation at small values of $\varepsilon$.(1,143 × 1,098 (109 KB)) - 09:43, 21 June 2013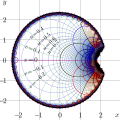
File:SuZex0map48small.png Coefficients $c$ are calculated with [[Mathematica]], from the [[asymptotic expansion]] at large $-z$, condition $~\mathrm{SuZex}(0)\!=\!1~$ and the [[ Formally, function [[SuZex]] is entire, and the Taylor series converges at any $z$; the range of approximation increase increasing number(1,230 × 1,230 (734 KB)) - 09:43, 21 June 2013
File:TaniaBigMap.png and indicates, how many significant digits does the truncated series return. [[Category:Asymptotic expansions]](851 × 841 (654 KB)) - 08:53, 1 December 2018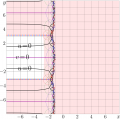
File:TaniaNegMapT.png [[Complex map]] of the truncation of the asymptotic expansion of the [[Tania function]] The truncation of the series gives the approximation shown in the figure.(1,773 × 1,752 (306 KB)) - 09:39, 21 June 2013
File:Matbug01.jpg Bug of the [[Mathematica]] routine [[Series]] at calculation of asymptotic expansion of the [[Bessel function]]. A = Series[BesselJ[0, x] Sqrt[Pi/2] x^(5/2)/(1 + x^2), {x, Infinity, 4}](1,165 × 872 (272 KB)) - 08:42, 1 December 2018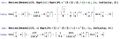
File:MathematicaBug01Fragment.jpg Series[BesselJ[0, Sqrt[x]] Sqrt[Pi x^(5/2)/2]/(1+x), {x,Infinity,2}] Series[BesselJ[0, x] Sqrt[Pi/2] x^(5/2)/(1+x^2), {x,Infinity,4}](1,086 × 349 (92 KB)) - 08:42, 1 December 2018
File:Sunem0map6.jpg (* Coefficients of the asymptotic expansion of function SuNem can be computed with the Mathematica code below m = 2; s[m] = Numerator[ Normal[Series[(T[F[m, -1/x^2]] - F[m, -1/x^2+1]) 2^((m+1)/2)/x^(m+2), {x,0,1}]]](2,615 × 2,594 (1.15 MB)) - 08:53, 1 December 2018
File:Sunem0mdp.jpg (* Coefficients of the asymptotic expansion of function SuNem can be computed with the Mathematica code below m = 2; s[m] = Numerator[ Normal[Series[(T[F[m, -1/x^2]] - F[m, -1/x^2+1]) 2^((m+1)/2)/x^(m+2), {x,0,1}]]](2,158 × 2,141 (822 KB)) - 08:53, 1 December 2018
