Search results
Create the page "Sqrt(2)" on this wiki! See also the search results found.

File:AuZexMapT.jpg z_type LambertWe(z_type z){ int n,m=100; z_type t=1./M_E+z; t*=2*M_E; t=sqrt(t); if( abs(z)<.2 ) return LambertWo(z);(4,367 × 4,326 (1.53 MB)) - 08:30, 1 December 2018
File:B271t.png DB b=sqrt(2); DO(n,N1){y=Y[n]; z=z_type(x,y); if(abs(z+2.)>.04)(1,609 × 1,417 (791 KB)) - 08:30, 1 December 2018
File:Besselj0map1T080.png - 9./4.)*u + 2.)* c; return (C+S)/sqrt(2.*M_PI*z);}(1,827 × 932 (1.7 MB)) - 09:41, 21 June 2013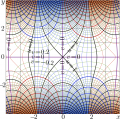
File:Besselj0mapT100.png - 9./4.)*u + 2.)* c; return (C+S)/sqrt(2.*M_PI*z);}(1,173 × 1,164 (1.45 MB)) - 09:41, 21 June 2013
File:Besselj1mapT080.png return s*z/2.;} f=M_PI/4.+z; c=cos(f); s=sin(f); a=sqrt(2./M_PI/z); t=1./(z*z);(2,056 × 1,048 (1.72 MB)) - 09:42, 21 June 2013
File:Besselk0mapT900.png +t*(6.50869783874735494e-12 - 2.40280754952443941e-12*L +t*(2.65978468063980854e-14 - 9.38596699032984143e-15*L(2,118 × 2,105 (1.62 MB)) - 09:41, 21 June 2013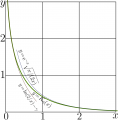
File:Besselk0plotT400.png $y\!=\! \exp(-x)\sqrt{\pi/(2x)}$ is shown with upper thin line, it approximates the function in t $y\!=\! \ln(2/x)-\mathrm {EulerGamma}$ is shown with lower thin line, it approcimates the(1,783 × 1,816 (189 KB)) - 09:41, 21 June 2013
File:CoshcmapT120.png if(Im(z)<0){if(Re(z)>=0){return I*log( z + sqrt(z*z-1.) );} else{return I*log( z - sqrt(z*z-1.) );}}(1,407 × 1,397 (1.47 MB)) - 09:41, 21 June 2013
File:DoyaconT70.png )))))); DO(n,2) s+=(z-ArcTania(s))/ArcTaniap(s); return s ; } z_type TaniaS(z_type z){int n; z_type s,t=z+z_type(2.,-M_PI);t*=2./9.; t=I*sqrt(t);(442 × 817 (98 KB)) - 09:39, 21 June 2013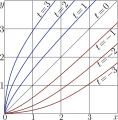
File:DoyaPlotT100.png z_type TaniaS(z_type z){int n; z_type s,t=z+z_type(2.,-M_PI);t*=2./9.; t=I*sqrt(t); if( fabs(Im(z))< M_PI && Re(z)<-2.51) return TaniaNega(z);(580 × 590 (77 KB)) - 08:34, 1 December 2018
File:E1efig09abc1a150.png $b\!=\!\sqrt{2}$ , right. for(m=-2;m<0;m+=2) {M(-4.7,m-.2) fprintf(o,"(%1d)s\n",m);}(2,234 × 711 (883 KB)) - 08:34, 1 December 2018
File:Esqrt2iterMapT.png [[Complex map]] of 1/3 th iteration of the [[exponential]] to [[base sqrt(2)]]. $T(x) = \Big(\sqrt{2}\Big){^z}= \exp_b(z)$(1,092 × 1,080 (1.36 MB)) - 09:43, 21 June 2013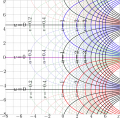
File:ExpQ2mapT.png [[Complex map]] of [[exponential]] to [[base sqrt2]], id est, $b=\sqrt{2}$; $u\!+\!\mathrm i v=\exp_{\sqrt{2}}(x\!+\!\mathrm i y)$(1,765 × 1,729 (1.15 MB)) - 08:35, 1 December 2018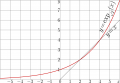
File:ExpQ2plotT.png [[Explicit plot]] of [[exponential]] to base $b\!=\!\sqrt{2} \approx 1.414213562373095$ The [[fixed point]]s $L\!=\!2$ and $L\!=\!4$ are solutions of the equation(2,512 × 1,744 (175 KB)) - 08:35, 1 December 2018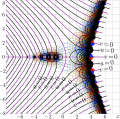
File:FacmapT500.png 1.01152306812684171, 1.51747364915328740, 2.26948897420495996, 3.00991738325939817, return s + log(2.*M_PI)/2. - z + (z+.5)*log(z);(2,355 × 2,334 (1.73 MB)) - 09:41, 21 June 2013
File:Fafo2test0.png Test image, used for the demonstration of the [[Fourier-2 transform]] and the Fourier-filtering of the images. The step of the grid is $\sqrt{\pi/16}=\sqrt{\pi} /4 \approx 0.443$(642 × 642 (5 KB)) - 09:39, 21 June 2013
File:Fafo2test1.png Modullus of the [[Fourier-2 transform]] of the bi–dimiensional real array [[File:Fafo2test0.png|128p The discrete implementation of the Fourier–2 transform approximates the integral transform $B$ of the function $A$ in th(642 × 642 (8 KB)) - 09:39, 21 June 2013
File:Fafo2test2.png The [[Fourier-2 transform]] $B$ of the function $A$ is determines with : $\displaystyle B(p,q)=\frac{1}{2\pi} \int \int \mathrm d x \mathrm d y \exp(-ipx-iqy) A(x,y)$(642 × 642 (6 KB)) - 09:39, 21 June 2013
File:Fafo2test3.png The [[Fourier-2 transform]] $B$ of the function $A$ is determines with : $\displaystyle B(p,q)=\frac{1}{2\pi} \int \int \mathrm d x \mathrm d y \exp(-ipx-iqy) A(x,y)$(642 × 642 (8 KB)) - 09:39, 21 June 2013
File:Filogbigmap100.png ...rm e$, which is the branch point; the second goes through the point $z=\pi/2$, where the fixed points are $\pm \mathrm i$. ...the cut, the function has real values; in particular, at $z=\ln\big(\sqrt{2}\big)$, there values are integer(2,870 × 2,851 (847 KB)) - 08:36, 1 December 2018