Base sqrt2

Map of exponent to base $b=\sqrt{2}$; lines of constant $u$ and lines of constant $v$ show $u+\mathrm i v=\exp_b(x+\mathrm i y)$

Map of Logarithm to base $b=\sqrt{2}$; lines of constant $u$ and lines of constant $v$ show $u+\mathrm i v=\log_b(x+\mathrm i y)$

Курвa $~y\!=\!\exp_{\sqrt{2}}(x)~$ и прямая $~y\!=\!x$

Base sqrt2 is article about functions that refer to base $b=\sqrt{2}$. These are:

Exponential and Logarithm to base $b$, id est, $~\exp_{\sqrt{2}}~$, $~\log_{\sqrt{2}}~$,

Tetration to base $b$ and other superexponentials to base $b$

Higher Ackermann functions to this base.

Base sqrt2 is considered by request from Henryk Trappmann; tetration to base sqrt2 happen to show some specific properties. Ansus had insisted that this tetration have specific kind of symmetry; and it costed efforts to convince him that the symmetry he suggests is only approximation, that holds with approximately 3 decimal digits.

About the name

Handling the article with robots happened to be difficult while the name of the article contains specific characters, in particular, parenthesis. For this reason, notation sqrt2 instead of sort(2) is used in the title.

Exponential and logarithm to base sqrt2

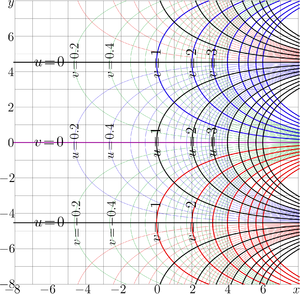
The complex map of the exponential to base $\sqrt{2}$ is shown in the upper figure; the map of logarithm to the same base is shorn in the second figure.

The exponential is entire periodic function with period $P=2\pi \mathrm i /\ln(\sqrt{2}) \approx$

The logarithm is holomorphic in the complex plane with cut along the negative part of the real axis. This cut is marked with dashed line in the picture.

In the whole complex plane except $z\le 0$, the relation $\exp_b\big( \log_b(z) \big)=z$ takes place.

Relation

$\log_b\big( \exp_b(z)\big) =z $

holds for $~ |\Im(z)|< \pi ~ / \ln(b)$

Exponential and logarithm to base sqrt2 are elemantary functions and can be easy expressed through the conventional exp and ln:

$\exp_b(z)=\exp\big(\ln(b) z\big)$

$\ln_b(z)=\ln(z)/\ln(b)$

Fixed points

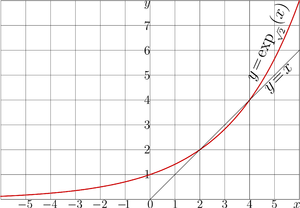
Exponential to base sqrt2 has two real fixed points, $L_1=2$ and $L_2=4$. These $L$ are solutions of equation

$\exp_b(L)=L$

The graphical solution of this equation is shown in figure at right. Each of these values оф $L$ can be used to built-up the refular iterate of the exponential to base $\sqrt{2}$, its superfunction and the corresponding Abel function.

Tetration to base sqrt2

Tetration to base $b$ is denoted as $\mathrm{tet}_b$

It is solution $F$ of the transfer equation

$F(z+1)=\exp_b\big(F(z)\big)$

with additional condition $\mathrm{tet}_b(0)=1$, holomorphic in the range $\{z\in \mathbb c : \Re(z)>-2\}$; it is assumed to be periodic function with period

$p=..$

ArcTetration to base sqrt2

ArcTetration to base $b$ is denoted as $\mathrm{ate}_b$

Other superfunctions

In addition to tetration, another real-holomorphic superexponentials to base $b=\sqrt{2}$ can be constructed. The choices are, first, which fixed point is used to built-up the regular iteration; and, in addition, in which direction is this superfunction supposed to approach the fixed point.