SdPow

Fig.1. Quadratic function (black curve) and two its superfunctions

Fig.2. $u\!+\mathrm i v=\mathrm{SdPow}_2(x\!+\mathrm i y)$

SdPow is specific superpower function, id est, the superfunction of the power function $~z\mapsto z^a\!=\!\exp(\ln(z) \,a)~$

For given parameter $a$,

$\mathrm{SdPow}_a(z)=\exp(a^z)$

Usually, it is assumed, that $a\!>\!1$.

Transfer function

Function $F\!=\!\mathrm{SdPow}_a$ is superfunction for the specific power function $T(z)\!=\!z^a$. The superfunction satisfies the transfer equation

$T(F(z))=F(z\!+\!1)$

For this specific transfer function $T$, the two real-holomorphix solutions are SuPow and SdPow:

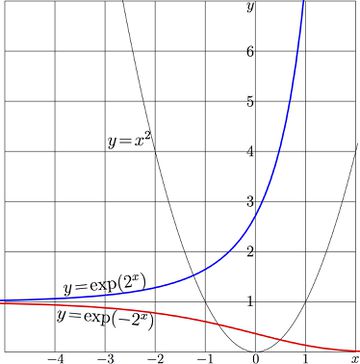
$\mathrm{SdPow}_a(z)=\exp(-a^z)$

$\mathrm{SuPow}_a(z)=\exp(a^z)$

For the power function both, the superfunctions and the Abel functions can be expressed as elementary functions. For $a\!=\!2$, these functions are who functions are shown in Fig.1.

For the same $a\!=\!2$, the complex map of function SdPow is shown in FIg.2.

Keywords

AdPow, Elementary function, Power function, SdPow, SuPow, Superfunction Superpower