File:Sunem0mdp.jpg
Original file (2,158 × 2,141 pixels, file size: 822 KB, MIME type: image/jpeg)
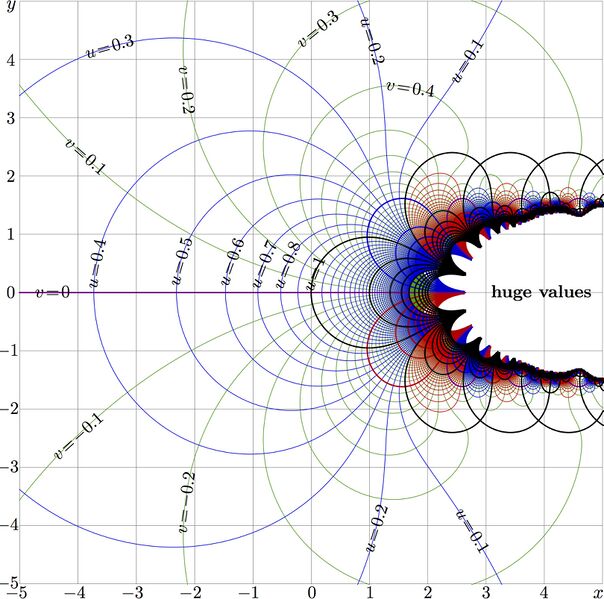
Complex map of function SuNem with parameter $q\!=\!0$;
$u\!+\!\mathrm i v=\mathrm{SuNem}_0(x\!+\!\mathrm i y)$
Description
Nemtsov function is polynomial of the special kind,
$\mathrm{Nem}_q(z)=z+z^3+qz^4$
where $q$ is positive parameter.
For the Nemtsov function, its superfunction SuNem is solution $F=\mathrm{SuNem}_q$ of the transfer equation
$F(z\!+\!1)=\mathrm{Nem}_q(F(z))$
whith specific behaviour at -infinity
$\displaystyle \mathrm{SuNem}_q(z) = \frac{1}{\sqrt{-2z}} \left(1+O\left( \frac{1}{\sqrt{-2z}} \right)\right)$
and specific value at zero, $\mathrm{SuNem}_q(0)=1$.
The Nemtsov function is suggested as an example of the transfer function, for wich the exotic iterates cannot be constructed with algorithms, presented in the First Russian version of the book Superfunctions.
References
Mathematica generator of the algorithm
(* Coefficients of the asymptotic expansion of function SuNem can be computed with the Mathematica code below *)
T[z_] = z + z^3 + q z^4
P[m_, L_] := Sum[a[m, n] L^n, {n, 0, IntegerPart[m/2]}]
A[1, 0] = -q; A[1, 1] = 0;
a[2, 0] = 0; A[2, 0] = 0;
F[m_, z_] := 1/(-2 z)^(1/2) (1 - q/(-2 z)^(1/2) + Sum[P[n, Log[-z]]/(-2 z)^(n/2), {n, 2, m}])
m = 2; s[m] = Numerator[ Normal[Series[(T[F[m, -1/x^2]] - F[m, -1/x^2+1]) 2^((m+1)/2)/x^(m+2), {x,0,1}]]]
t[m] = Numerator[Coefficient[Normal[s[m]], x] ]
sub[m] = Extract[Solve[t[m] == 0, a[m, 1]], 1]
SUB[m] = Simplify[sub[m]]
f[m, z_] = ReplaceAll[F[m, z], SUB[m]]
m = 3
s[m] = Simplify[ ReplaceAll[ Series[(T[F[m, -1/x^2]] - F[m, -1/x^2+1]) 2^((m+3)/2)/x^(m+3), {x,0,0}], SUB[m-1]]];
t[m] = ReplaceAll[Normal[s[m]], Log[x] -> L];
u[m] = Table[ Coefficient[t[m] L, L^n] == 0, {n, 1, 1 + IntegerPart[m/2]}];
tab[m] = Table[a[m, n], {n, 0, IntegerPart[m/2]}];
sub[m] = Extract[Solve[u[m], tab[m]], 1]
SUB[m] = Join[SUB[m-1], sub[m]];
(* and the same for other m *)
Clear[m]; A[m_, n_] := ReplaceAll[a[m, n], sub[m]]
For[m = 1, m < 37,
For[n = 0, n < (m + 1)/2,
Print["A[", m, "][", n, "]=", CForm[N[ReplaceAll[HornerForm[A[m, n], q], {q^2 -> K, q -> Q}]]], ";"]; n++]; m++;]
(* The resulting array of coefficients should be stored in file sunema.txt, it should be included at the compilation of the code below *)
C++ generator of the map
// Files ado.cin, conto.cin, sune.cin, sunema.txt should be loaded in order to compile the code below
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
//using namespace std;
#include <complex>
typedef std::complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "conto.cin"
DB Q=0.;
z_type nem(z_type z){ return z*(1.+z*z*(1.+z*Q)); }
z_type nem1(z_type z){ return 1.+z*z*(3.+z*(4.*Q)); } // WARNING: Q is global!
#include "sune.cin"
DB SUNo=0; // should be reassigned
z_type sunem(z_type z){ return sune(z + SUNo);}
int main(){ int Max; int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;
// DB rr,ti;
co(); // Evaluate soefficients of the expansion
x=0; DO(n,60) { y=Re(sune(x)); x-= y-1.; printf("%19.16lf %19.16lf\n", x,y);}
SUNo=x;
printf("A[2][0]= %9.5lf , A[2][1]=%9.5lf\n",A[2][0],A[2][1]);
printf("A[3][0]= %9.5lf , A[3][1]=%9.5lf\n",A[3][0],A[3][1]);
int M=501,M1=M+1;
int N=501,N1=N+1;
DB X[M1],Y[N1]; DB *g, *f, *w; // w is working array.
g=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
f=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
w=(DB *)malloc((size_t)((M1*N1)*sizeof(DB)));
char v[M1*N1]; // v is working array
//DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
//char v[M1*N1]; // v is working array
FILE *o;o=fopen("sunem0md.eps","w");ado(o,1008,1008);
fprintf(o,"504 504 translate\n 100 100 scale 2 setlinecap\n");
DO(m,M1) X[m]=-5.+.02*(m-.5);
DO(n,N1) Y[n]=-5.+.02*(n-.5);
for(m=-5;m<6;m+=1){ M(m,-5)L(m,5)}
for(n=-5;n<6;n+=1){ M(-5,n)L(5,n)}
fprintf(o,".003 W 0 0 0 RGB 2 setlinecap S\n");
DO(m,M1)DO(n,N1){g[m*N1+n]=9999999; f[m*N1+n]=9999999;}
DO(m,M1){x=X[m]; if(m/10*10==m) printf("run at x=%6.3f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y);
c=sunem(z);
//d=sune(z);
//p=abs(c-d)/abs(c+d); p=-log(p)/log(10.);
p=Re(c); q=Im(c);
//if(p>-85 && p<85) g[m*N1+n]=p;
if(p>-1001 && p<1001 &&
q >-1001 && q<1001 ) { g[m*N1+n]=p; f[m*N1+n]=q; }
}}
//M(-2,0) L(0,0) M(tr,ti)L(0,0)L(tr,-ti)
//fprintf(o,".002 W 1 1 0 RGB 0 setlinecap S\n");
fprintf(o,"1 setlinejoin 1 setlinecap\n");
p=6.;q=.6;
//#include"plofu.cin"
for(m=-5;m<5;m++)for(n=1;n<10;n+=1)conto(o,f,w,v,X,Y,M,N, (m+.1*n),-q,q);
fprintf(o,".01 W 0 .6 0 RGB S\n");
for(m=0;m<5;m++) for(n=1;n<10;n+=1)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q,q);
fprintf(o,".01 W .9 0 0 RGB S\n");
for(m=0;m<5;m++) for(n=1;n<10;n+=1)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q,q);
fprintf(o,".01 W 0 0 .9 RGB S\n");
for(m= 1;m<11;m++) conto(o,f,w,v,X,Y,M,N,(0.-m),-p,p);fprintf(o,".023 W .8 0 0 RGB S\n");
for(m= 1;m<11;m++) conto(o,f,w,v,X,Y,M,N,(0.+m),-p,p);fprintf(o,".023 W 0 0 .8 RGB S\n");
conto(o,f,w,v,X,Y,M,N,(0. ),-p,p);fprintf(o,".023 W .5 0 .5 RGB S\n");
for(m=-10;m<11;m++)conto(o,g,w,v,X,Y,M,N,(0.+m),-p,p);fprintf(o,".023 W 0 0 0 RGB S\n");
/*
conto(o,g,w,v,X,Y,M,N,15.5,-1,1);fprintf(o,".02 W 1 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N,15.,-p,p);fprintf(o,".04 W 0 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N,14.,-p,p);fprintf(o,".02 W 0 1 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N,13.,-p,p);fprintf(o,".02 W 1 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N,12.,-p,p);fprintf(o,".04 W 0 0 .7 RGB S\n");
conto(o,g,w,v,X,Y,M,N,11.,-p,p);fprintf(o,".02 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N,10.,-p,p);fprintf(o,".02 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N,9.,-p,p);fprintf(o,".04 W 0 .6 .8 RGB S\n");
conto(o,g,w,v,X,Y,M,N,8.,-p,p);fprintf(o,".02 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N,7.,-p,p);fprintf(o,".02 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N,6.,-p,p);fprintf(o,".04 W 0 .6 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N,5.,-p,p);fprintf(o,".02 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N,4.,-p,p);fprintf(o,".02 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N,3.,-p,p);fprintf(o,".04 W 1 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N,2.,-p,p);fprintf(o,".02 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N,1.,-p,p);fprintf(o,".05 W .5 0 0 RGB S\n");
*/
//M(-2,0) L(0,0) M(tr,ti)L(0,0)L(tr,-ti)
//fprintf(o,".004 W 1 1 0 RGB 0 setlinecap S\n");
fprintf(o,"showpage\n%cTrailer",'%'); fclose(o);
system("epstopdf sunem0md.eps");
system( "open sunem0md.pdf"); //mac
//for(m=-40;m<0;m++) {x=m; y=Re(sun(x)); t=Re(nem(sun(x-1.))); printf("%6.1lf %18.15lf %18.15lf %18.15lf\n", x,y,t,y-t);}
return 0;
}
Latex generator of the labels
%\documentclass[12pt]{article}
\documentclass{mcom-l}
\usepackage{graphics}
\paperwidth 1040pt
\paperheight 1032pt
\usepackage{geometry}
\usepackage{rotating}
\textwidth 1260pt
\textheight 1260pt
\topmargin -94pt
\oddsidemargin -72pt
\parindent 0pt
\pagestyle{empty}
\newcommand \ing {\includegraphics}
\newcommand \sx {\scalebox}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\begin{document}
\begin{picture}(1038,1030)
%\put(50,40){\ing{sunem10q10ma6s}}
%\put(24,20){\ing{nem120ma}}
\put(30,20){\ing{sunem0md}}
\put(11,1015){\sx{3.2}{$y$}}
\put(11,917){\sx{3}{$4$}}
\put(11,817){\sx{3}{$3$}}
\put(11,717){\sx{3}{$2$}}
\put(11,617){\sx{3}{$1$}}
\put(11,517){\sx{3}{$0$}}
\put(-6,417){\sx{3}{$-1$}}
\put(-6,317){\sx{3}{$-2$}}
\put(-6,217){\sx{3}{$-3$}}
\put(-6,117){\sx{3}{$-4$}}
\put(-6, 17){\sx{3}{$-5$}}
\put( 9, 0){\sx{3}{$-5$}}
\put(109, 0){\sx{3}{$-4$}}
\put(209, 0){\sx{3}{$-3$}}
\put(309, 0){\sx{3}{$-2$}}
\put(409, 0){\sx{3}{$-1$}}
\put(530, 0){\sx{3}{$0$}}
\put(630, 0){\sx{3}{$1$}}
\put(730, 0){\sx{3}{$2$}}
\put(830, 0){\sx{3}{$3$}}
\put(930, 0){\sx{3}{$4$}}
\put(1022,0){\sx{3.2}{$x$}}
%
\put(788,884){\sx{3}{\rot{57} $u\!=\!0.1$\ero}}
\put(620,998){\sx{3}{\rot{-73} $u\!=\!0.2$\ero}}
\put(150,929){\sx{3}{\rot{16} $u\!=\!0.3$\ero}}
\put(166,532){\sx{3}{\rot{79} $u\!=\!0.4$\ero}}
\put(308,536){\sx{3}{\rot{74} $u\!=\!0.5$\ero}}
\put(392,535){\sx{3}{\rot{70} $u\!=\!0.6$\ero}}
\put(446,531){\sx{3}{\rot{68} $u\!=\!0.7$\ero}}
\put(486,530){\sx{3}{\rot{68} $u\!=\!0.8$\ero}}
\put(538,526){\sx{3}{\rot{68} $u\!=\!1$\ero}}
%
\put(642,76){\sx{3}{\rot{72} $u\!=\!0.2$\ero}}
\put(784,148){\sx{3}{\rot{-59} $u\!=\!0.1$\ero}}
%
\put(664,876){\sx{3}{\rot{-9} $v\!=\!0.4$\ero}}
\put(520,946){\sx{3}{\rot{39} $v\!=\!0.3$\ero}}
\put(308,916){\sx{3}{\rot{-84} $v\!=\!0.2$\ero}}
\put(110,782){\sx{3}{\rot{-41} $v\!=\!0.1$\ero}}
\put(60,518){\sx{3}{\rot{0} $v\!=\!0$\ero}}
\put(846,518){\sx{3}{\rot{0} \bf huge values\ero}}
\put(100,236){\sx{3}{\rot{42} $v\!=\!-0.1$\ero}}
\put(321, 110){\sx{3}{\rot{82} $v\!=\!-0.2$\ero}}
%
\end{picture}
\end{document}
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 06:14, 1 December 2018 |  | 2,158 × 2,141 (822 KB) | Maintenance script (talk | contribs) | Importing image file |
You cannot overwrite this file.
File usage
The following page uses this file: