AuPow
AuPow is specific Abelpower function, id est, the specific Abel function for the Power function.
AuPow can be expressed as elementary function,
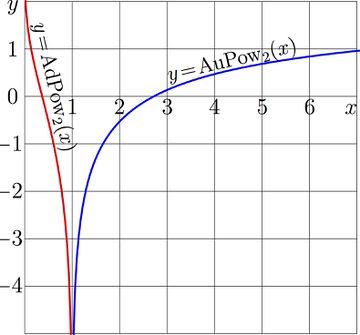
\(\mathrm{AdPow}_a(z)=\log_a(\ln(z))\)
Where \(a\) is parameter. Usually, it is assumed that \(a\!>\!0\).
AuPow is inverse function of SuPow, that, in its turn, is superfunction of the power function.
AdPow and AuPow
Another abelfunction for the power function is called AdPow;
\(\mathrm{AdPow}_a(z)=\log_a(\ln(1/z))\)
AdPow is related with AuPow function with simple relation:
\(\mathrm{AdPow}_a(z)=\mathrm{AuPow}_a(1/z)\)
For \(a\!=\!2\), both functions AdPow and AuPow are shown in Fig.1
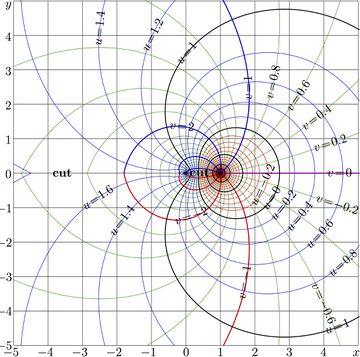
For the same \(a\!=\!2\), complex map of function AuPow is shown in Fig.2.
Inverse function
For AuPow, the inverse function is SuPow, that is superpower function, id est, superfunction of the power function:
\(\mathrm{AuPow}_a=\mathrm{SuPow}_a^{-1}\)
SuPow satisfies the Transfer equation
\(\mathrm{SuPow}_a(z\!+\!1)=\mathrm{SuPow}_a(z)^a\)
SuPow is elementary function,
\(\mathrm{SuPow}_a(z)= \exp(a^z)\)
Applications
AuPow appears as example of the Abel function that can be expressed as elementary function. This allows to trace evaluation of superfunction through the regular iteration; the fixed point unity can be used for the calculation.
This example seems to be important for the book Superfunctions.
References
Keywords
Abel function AdPow Abel function Elementary function Power function SdPow SuPow Superfunctions SdPow Superfunctions