Hermite polynomial

Hermite polynomial appears at the solution of the Stationary Schroedinger equation with quadratic potential. Also, the Hermite polynomials appear in the Hermite Gauss modes.
The \(m\)th Hermite polynomial can be defined as
\(H_m(x)=(-1)^m \exp(-x^2) \partial_x^m \exp(-x^2)\)
The \(m\)th Hermite polynomial is denoted with \(H_m(x)=\mathrm{HermiteH}[m,x]\).
In particular,
\(H_0(x)=1\),
\(H_1(x)=2x\),
\(H_2(x)=4x^2-2\)
Recurrent relations
\(H_{n+1}(x)=2xH_n(x)-2nH_{n-1}(x)\)
\(H_n'(x)=2nH_{n-1}(x)\)
Orthogonality
Hermite polynomials are orthogonal at the whole real axis with weight \(U(x)=\exp(-x^2)\) :
\(\displaystyle \int_{-\infty}^{\infty} \exp(-x^2)\, H_m(x)\, H_n(x)\, \mathrm d x= 2^n\, n!\, \sqrt{\pi}\, \delta_{m,n}\)
The normalisation factor \(~ ~ ~ N_n=2^n\, n!\, \sqrt{\pi}\)
is used to define normalised hermites
\(\displaystyle h_n(z)= \frac{1}{\sqrt{N_n}} \mathrm{HermiteH}[n,x]=\frac{H_n(x)}{\sqrt{N_n}}\)
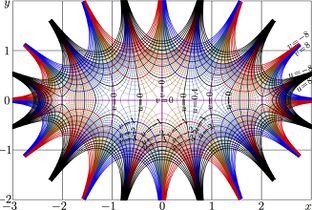
Explicit plot of \(h_n\) for \(n=2\) .. \(6\) is hown in figure at the top. Below, the complex map of \(h_6\) is shown.
Oscillator functions
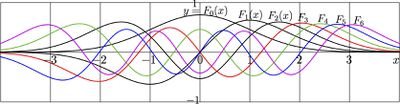
\(F_n(x)=h_n(x) \, \exp(-x^2/2)\) \(=N_n^{-1/2}\, H_n(x)\, \exp(-x^2/2)\)
appear both, as solutions for the stationary Schroedinger equations for the Harmonic oscillator and at the Hermite Gauss modes. Explicit plot \(y\!=\!F_n(x)\) is shown in figure at right for \(n=0 .. 6\).
The oscillator function \(f_n\) is solution of the equation
\(F''(x)+(2n\!+\!1-x^2)\, F(x) = 0\)
that is stationary Schroedinger equation of a particle of mass unity in the quadratic potential; then, \(x^2\) can be interpreted as twiced potential, and expression \(2n\!+\!1\) can be interpreted as energy of the eigenstate of the system.
Hermite number
There is special name for
\(H_n=H_n(0)=\mathrm{HermiteH}[n,0]\).
It is called Hermite number; originally, \(H_n\) is defined only for integer \(n\). [1]
\(\displaystyle H_n= \frac {2^n \sqrt{\pi}} {\displaystyle \mathrm{Factorial}\left(- \frac{1\!+\!n}{2}\right)}\) \(\displaystyle = \left\{ \begin{array}{ccc} 0 & \mathrm{for ~ odd} & n \\ \displaystyle (-1)^{n/2} \frac{n!}{(n/2)!} &\mathrm{for ~ even} & n \end{array} \right.\)
C++ implementation
For fast generation of complex diagrams, it may have sense to use the fast implementation for the Hermite polynomials (with already pre-calculated coefficients). The implementation of \(H_n(x)\) for \(0<n<14\) is suggested below:
DB HermitH0[7][7]= // COEFFICIENTS OF EVEN HERMITEH
{{1, 0, 0, 0, 0, 0, 0},
{-2, 4, 0, 0, 0, 0, 0},
{12, -48, 16, 0, 0, 0, 0},
{-120, 720, -480, 64, 0, 0, 0},
{1680, -13440, 13440, -3584, 256, 0, 0},
{-30240, 302400, -403200, 161280, -23040, 1024, 0},
{665280, -7983360, 13305600, -7096320, 1520640, -135168, 4096}};
DB HermitH1[7][7]= // COEFFICIENTS OF ODD HERMITEH
{{2, 0, 0, 0, 0, 0, 0},
{-12, 8, 0, 0, 0, 0, 0},
{120, -160, 32, 0, 0, 0, 0},
{-1680, 3360, -1344, 128, 0, 0, 0},
{30240, -80640, 48384, -9216, 512, 0, 0},
{-665280, 2217600, -1774080, 506880, -56320, 2048, 0},
{17297280, -69189120, 69189120, -26357760,4392960, -319488, 8192}};
DB HermitH(int n,DB x){ int m,M; DB s, xx;
if(n==0) return 1.;
if(n==1) return x+x;
if(n>13) {printf("hermite number %2d is not yet implemented (max. is 13)\n consider to stop..",n); getchar(); return 0;}
xx=x*x; //printf("Hernith called with n=%3d x=%8.2lf\n",n,x);
if(n/2*2==n){M=n/2; s=0.;for(m=M;m>0;m--) {s+=HermitH0[M][m]; s*=xx;}
return HermitH0[M][0]+s; }
else{ M=(n-1)/2; s=0.; for(m=M;m>0;m--) {s+=HermitH1[M][m]; s*=xx;}
return (HermitH1[M][0]+s)*x; }
}
References
- ↑ http://mathworld.wolfram.com/HermiteNumber.html Weisstein, Eric W. "Hermite Number." From MathWorld--A Wolfram Web Resource.
http://mathworld.wolfram.com/HermitePolynomial.html Weisstein, Eric W. "Hermite Polynomial." From MathWorld--A Wolfram Web Resource. (2016)